题解 洛谷 P3294 [SCOI2016]背单词

题目

题目

凤老师告诉 Lweb ，我知道你要学习的单词总共有 n 个，现在我们从上往下完成计划表，对于一个序号为 x 的单词（序号 1...x-1 都已经被填入）：
1. 如果存在一个单词是它的后缀，并且当前没有被填入表内，那他需要吃 n*n 颗泡椒才能学会；
2. 当它的所有后缀都被填入表内的情况下，如果在 1...x-1 的位置上的单词都不是它的后缀，那么你吃 x 颗泡椒就能记住它；
3. 当它的所有后缀都被填入表内的情况下，如果 1...x-1的位置上存在是它后缀的单词，所有是它后缀的单词中，序号最大为 y ，那么你只要吃 x-y 颗泡椒就能把它记住。
请你帮助 Lweb ，寻找一种最优的填写单词方案，使得他记住这 n 个单词的情况下，吃最少的泡椒。

思路

分析

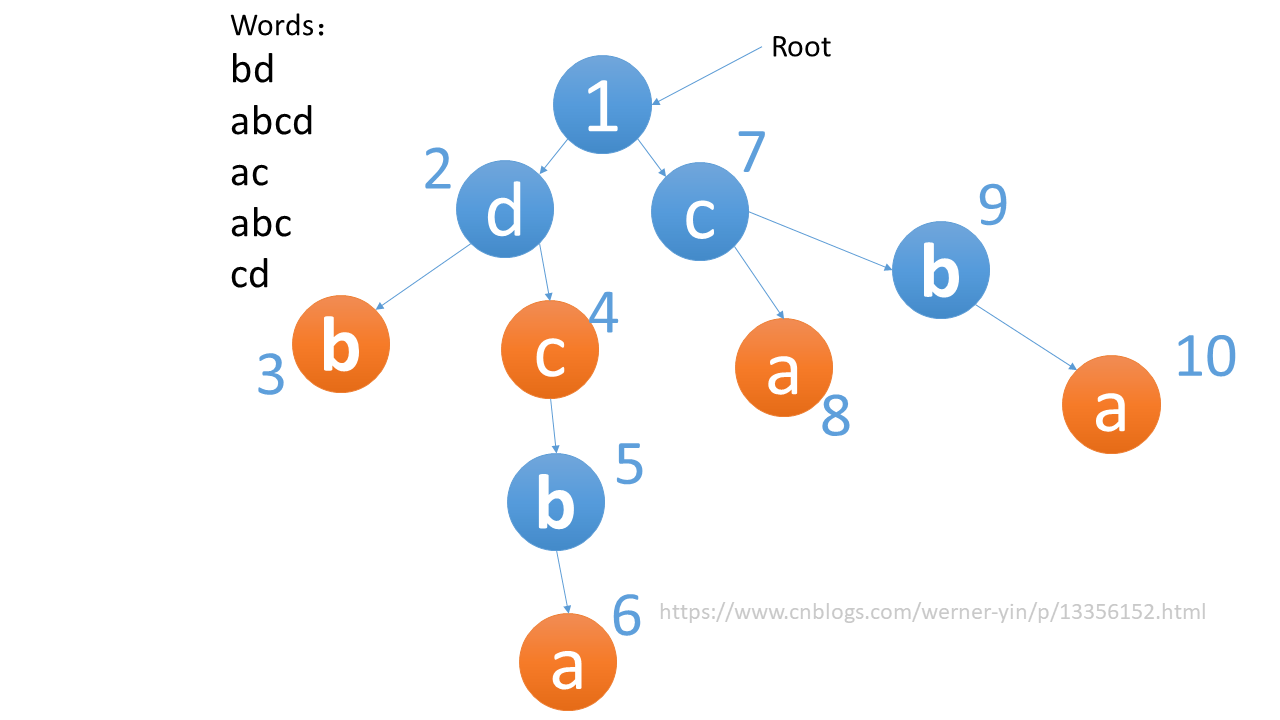
因为后缀，我们可以想到字典树，但此题反向建立字典树。如图：

其中，橙色的节点表示结尾。

void insert(char *a){
	int ls = strlen(a+1),p = 1;
	for(int i = ls;i >= 1;i--){
		int x = a[i] - 'a';
		if(!trie[p].son[x]) trie[p].son[x] = ++cnt;
		p = trie[p].son[x];
	}
	trie[p].en ++;
}

仔细理解题意后（我居然开始理解错了） ，我们可以发现：

1. 对于情况1，我们应该避免，可以按照字典树从根到子节点遍历来解决，这样保证每次背单词 a 时，它的后缀已经背了。

2. 情况2意味着这个单词只有一个字符，是情况3的特殊版本。

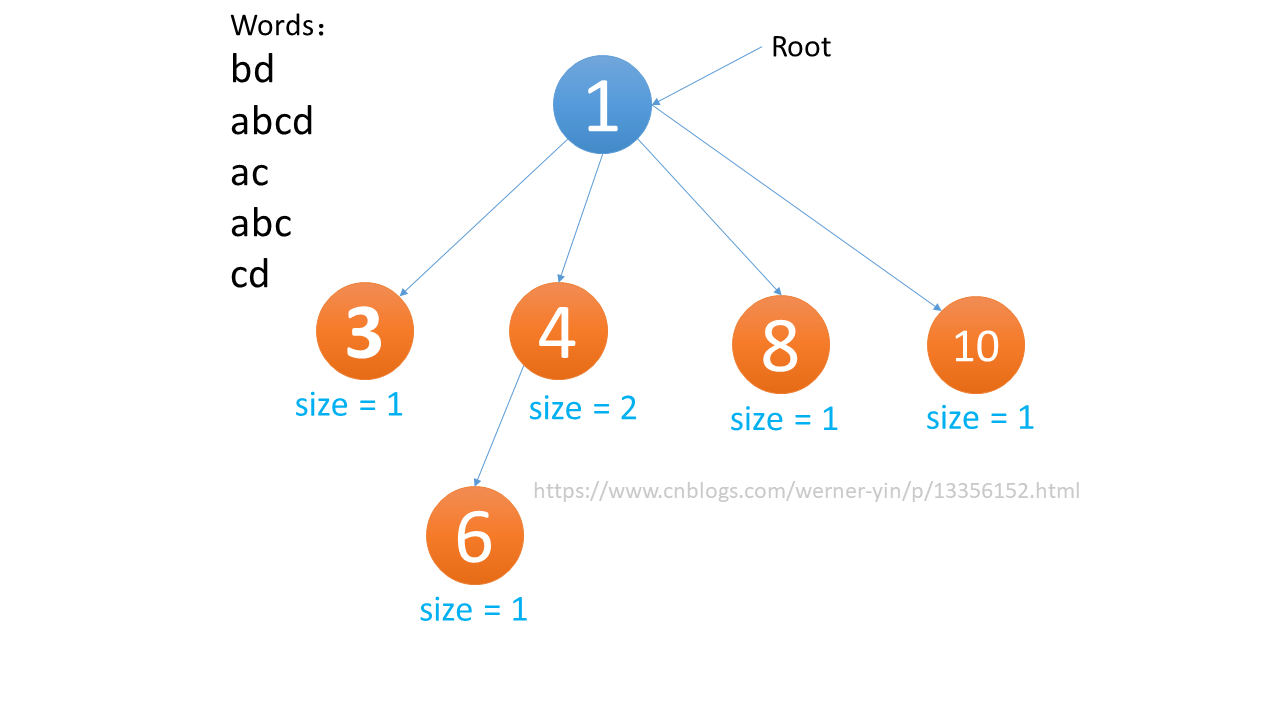
因为只有背单词的顺序对答案有影响，因此，我们可以先重构字典树,把不是单词结尾的节点删去。

这样，每个橙色的节点就代表一个单词。

vector <int> g[MAXN];
//重建树
void rebuild(int x){//注意 1 号节点要提前标为单词节点
	if(trie[x].en && x){
		g[trie[x].las].push_back(x);
		trie[x].las = x;
	}
	for(int i = 0;i < 26;i++) if(trie[x].son[i]){
		int y = trie[x].son[i];
		trie[y].las = trie[x].las;
		rebuild(y);
	}
}

最后一步重要的贪心：

我们发现更新完一个父亲节点后，一定要更新完它的子树，这样每次更新的代价可以尽可能的小。

但如果有多个子树呢？

我们要考虑更新子树顺序。

我们先用dfs求出每个子树大小。

在拿出这个重构的树来考虑：

我们可以发现，子树大小更小的子树应该先更新。

证明

为什么应该先更新（背）子树大小更小的子树？

我们已用图做出了解答，这部分可跳过。

因为一个子树一定时连着更新的，而更新的顺序仅对更新儿子节点代价有影响，因此，决定更新儿子节点代价的是在它前面更新（父亲节点后）了多少个节点。

这可以转化成我们熟悉的打水问题。

n 个人打水，每个人有一个打水时长，在某人打水时，其他未打水的人必须等待，求一种方案使所有人等待时间之和最短。

显然，此类问题答案肯定是先让打水时间更短的人打水。

此题中，打水时长即子树大小，等待时间之和类似于更新这些儿子节点的代价，于是应该先更新子树大小更小的子树。

代码

#define ll long long
using namespace std;

const int MAXN = 5.1e5+10;
const int MAXS = 5e5+10;

struct Trie{
	int son[26],en,las;
	ll val;
}trie[MAXN];

int n,cnt = 1;
ll ans,num = 0,siz[MAXN];
vector <int> g[MAXN];

// 记得long long

void insert(char *a){ //倒序插入
	int ls = strlen(a+1),p = 1;
	for(int i = ls;i >= 1;i--){
		int x = a[i] - 'a';
		if(!trie[p].son[x]) trie[p].son[x] = ++cnt;
		p = trie[p].son[x];
	}
	trie[p].en ++;
}

void rebuild(int x){//重建树
	if(trie[x].en && x){
		g[trie[x].las].push_back(x);
		trie[x].las = x;
	}
	for(int i = 0;i < 26;i++) if(trie[x].son[i]){
		int y = trie[x].son[i];
		trie[y].las = trie[x].las;
		rebuild(y);
	}
}

bool cmp (int a,int b){ return siz[a] < siz[b];}

void dfs(int x){//算子树大小
	siz[x] = 1;
	for(int i = 0;i < g[x].size();i++){
		dfs(g[x][i]);
		siz[x] += siz[g[x][i]];
	}
	sort(g[x].begin(),g[x].end(),cmp);
}

void getans(int x){//求出次序，算出答案
	ll dfn = num++;
	for(int i = 0;i < g[x].size();i++){
		ans += num - dfn;
		getans(g[x][i]);
	}
	return;
}

int main (){
	scanf("%d",&n);
	for(int i = 1;i <= n;i++){
		char a[MAXS];
		scanf("%s",a+1);
		insert(a);
	}
	trie[1].en = 1; //注意要先标记一下，以免出错（要在重建树中用到）
	rebuild(1);
	dfs(1);
	getans(1);
	printf("%lld",ans);
	return 0;
}

---

Tips: 允许转载，但请附上原博客地址：https://www.cnblogs.com/werner-yin/p/solution-P3294.html ，谢谢支持！