AGC 做题合集 #3
- "AGC029D Grid game"[1]
- "AGC021D Reversed LCS"[2]
- "AGC035E Develop"[3]
- "AGC017F Zigzag"[4]
- "AGC025E Walking on a Tree"[5]
- "AGC052D Equal LIS"[6]
- "AGC003E Sequential operations on Sequence"[7]
- "AGC006C Rabbit Exercise"[8]
- "AGC007D Shik and Game"[9]
- "AGC007E Shik and Travel"[10]
AGC029D Grid game
高木和青木正在玩一个游戏。
具体地说，他们有一个 \(H\times W\) 的矩阵，上面有 \(N\) 个障碍物。
在起点 \((1,1)\) 处有一颗小石子，高木先手，和青木将轮流进行以下操作：
- 假设当前石子所在的位置为 \((x,y)\) ，那么如果是轮到高木，他可以选择将石子移动到 \((x+1,y)\) 或者不移动。青木可以将石子移动到 \((x,y+1)\) 或者不移动。
- 石子移动到的地方不能是障碍物或者矩阵外面。
当一轮操作中高木和青木都没有移动石子时，游戏结束。
现在，高木想尽可能地让游戏轮数变多，而青木则会尽可能地让游戏轮数变少。
请问在双方都采取最优策略地情况下，会进行几轮游戏（最后一轮无法操作也算做一次）。
\(H, W \le 2\times 10^5, 0 \le N \le 2\times 10^5\)。
可以直接秒的大水题。
显然只要看出高木必须移动之后就没有任何难点了。
考虑到了以 \(i\) 轮，同时处理出最远可以到的列，那么如果有一个障碍是可以碰到的，那么青木一定会让高木撞上然后结束游戏。 ↩︎
AGC021D Reversed LCS
定义一个字符串 \(T\) 权值为 \(T\) 和 \(T'\)（翻转） 的最长公共子序列长度。
你现在有一个 \(S\)，你可以修改任意 \(k\) 个字符，求最大权值。
\(k \le |S| \le 300\)。
结论：这个求的是最长回文子序列长度。证明不会。
直接区间 DP 即可。 ↩︎
AGC035E Develop
在黑板上写有 \(-10^{18}\) 到 \(10^{18}\) 中的所有整数，每次你可以选中一个 \([ 1 , N]\) 中还在黑板上的整数 \(x\)，把它擦去并补写上 \(x − 2\) 与 \(x + K\)（如果原来不存在的话）。你可以进行这个操作任意次（可以不进行），求最终黑板上数字的可能状态有多少种，答案对 \(M\) 取模。
\(1\leq K \leq N \leq 150 , 10^8\leq M\leq 10^9\)。
又是猜对了结论但是不会维护。
首先结论是：
对于每个点 \(x\)，向 \(x - 2, x + K\) 连边，我们取出所有删去的点的导出子图，这个图必须是一个 \(\rm DAG\) 才是合法的。
连边是钦定 \(x - 2, x + K\) 在 \(x\) 后面删掉，只要不出现环形依赖就不会有问题。
考虑计数，对于 \(K\) 为偶数，我们就是可以奇偶分别考虑，要求不能形成 \(\frac{K}{2} + 1\) 个同时被擦除的元素即可。
对于奇数，蒯张图，（\(n = 12, K = 3\)）我们考虑出现的环的状况（对于奇数，将 \(i, i + K\) 放在一起）：
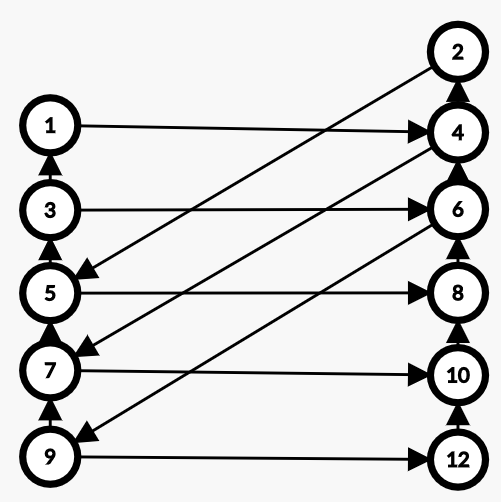
对于一个环，一定是从 \(a\) 出发，向上走若干步，然后向右走若干步，再向上走若干步，最后回来。（例如 \(9 \to 7 \to 5 \to 8 \to 6 \to 9\)）
考虑一层一层地 DP，设 \(f(i, j, k)\) 表示到了第 \(i\) 层，（我们把 \(x, x +K\) 的数当做一层，然后这个 DP 要预处理前面单着的数）从当前左部点出发最长可以走的路是 \(j\)（向上走若干步，然后向右走若干步，再向上走若干步 的长度），右边最长连续的长度为 \(k\)（方便 \(j\) 的转移）。
转移的时候讨论即可，具体看代码的注释。 ↩︎
AGC017F Zigzag
- 给定一个 \(N\) 层的三角形图，第 \(i\) 层有 \(i\) 个节点。
- 第 \(i\) 层的节点，从左到右依次标号为 \((i, 1), (i, 2), \ldots , (i, i)\)（具体如上图所示）。
- 你需要从 \((1, 1)\) 往下画 \(M\) 条折线。
- 对于每条折线的每一个小段，你可以从 \((i, j)\) 画到 \((i + 1, j)\) 或者 \((i + 1, j + 1)\)。
- 同时你还必须保证第 \(i\) 条折线的任何一个位置必须不能处在第 \(i - 1\) 条折线的左侧，它们必须按照从左到右的顺序排列。
- 有 \(K\) 条限制，每条限制形如 \((A_i, B_i, C_i)\)。
- 表示第 \(A_i\) 条折线处于位置 \((B_i, j)\) 时，下一小段必须走向 \((B_i + 1, j + C_i)\)，也就是当 \(C_i = 0\) 时向左，当 \(C_i = 1\) 时向右。
- 询问不同的折线画法的方案数，对 \({10}^9 + 7\) 取模。
- \(1 \le N, M \le 20\)，\(0 \le K \le M (N - 1)\)。其它变量在合理范围内。
如果一层一层地决策进行状压 DP，那么就是 \(\mathcal O(4^n n)\) 的。但是我们可以试着转换一下计数顺序！于是考虑一条一条线段分配位置！
我们把上次的线段的路线记作一个二进制数，如果第 \(i\) 位为 \(1\)，那么就代表在 \(i\) 层的时候向右走了。
当前这一条的线段的方案只要倒着前缀和的字典序 \(\ge\) 上一条的即可（因为最初一步为最低位，因此略有不同），如果暴力地 DP，还是 \(\mathcal O(4^nn)\)，但是转移到了 \(\mathcal O(1)\) 了！
我们接着可以发现，如果完全暴力地 DP，很多信息没有利用到，如果我们决策这一条线的路线的时候考虑一层一层地计算呢？可以发现，我们不能很好地处理字典序的问题，然后可以发现我们可以直接记录我们之后可以选择的范围！
具体地，我们要枚举第 \(i\) 层，以及上一次决策导致的我们可以选择范围的状态为 \(s\)，记 \(s\) 的第 \(i\) 位为 \(s[i]\)，如果：
-
如果我们这一层选择走左边 \(0\)，只要 \(s[i] = 0\) 即可，然后转移到 \(s\)。
-
如果我们走右边 \(1\)：
- 如果 \(s[i] = 1\)，那么可选范围还是 \(s\)，两个重合了。
- 如果 \(s[i] = 0\)，那么意味着我们一直到 \(i\) 下一个 \(1\) 处都可以选择 \(0\)，于是把 \(s\) 第 \(i\) 位置后面的第一个 \(1\) 设为 \(0\)，然后把 \(s[i]\) 设为 \(1\)，就是新的可选范围了！
AGC025E Walking on a Tree/ 校内考试 6.7 疯狂路径（path）
给定一棵 \(n\) 个节点的树和 \(m\) 条树上的路径，要求为每一条路径定向。
第 \(i\) 条树边 \((a_i, b_i)\) 的权值为满足下述条件的条数：
- 被某条路径沿 \(a_i\to b_i\) 方向经过。
- 被某条路径沿 \(b_i\to a_i\) 方向经过。
求最大权值和并给出 \(m\) 条路经的定向方案，多组方案合法输出任意一组即可。
\(n,m\leqslant 2000\)。加强：\(n, m \le 1 \times 10^5\)。
一个比较有意思的结论题。
考虑答案的上界，一定是 \(\sum \min\{每条边覆盖次数, 2\}\)，考虑达到上界：
每次选出一个叶子，然后考虑所有以它开始的路径，如果没有则不管，只有一条，则如何选择结果不变，将这个路径放到它父亲上面皆可；如果有两条以上，任意选择两条，这两条路径的方向一定是相反的，设路径为 \((u, a), (u, b)\)，我们新建一条路径 \((a, b)\)，删去这两条路径，并将其他路径放到父亲上去决策，然后根据 \((a, b)\) 的情况，如果 \((a, b)\) 不反向，那么 \((u, a)\) 反向，\((u, b)\) 不反向，反之亦然。
为什么可以新建这条路径呢？因为这样 \((u, a), (u, b)\) 和 \((a, b)\) 不相交的部分是不重要的，怎么样都是合法，我们只关心 \((a, b)\) 路径，同时这样可不会影响其他叶子的状态。
这个是一个比较暴力的构造，时间复杂度为 \(\mathcal O(n^2)\)，考虑优化：
首先反向关系的继承可以通过带权并查集完成，我们的复杂度瓶颈在于怎么将边给传上去，这个可以通过链表完成。
然后细节有亿点多，至少用了大半个下午肉眼盯傻了，但是上了对拍就可以发现很多问题！
一些细节：
- 判断取出来的边是否合法。
- 颜色关系的继承可能要自己在纸上面多画画。
- 注意取出来的对应的 \((u, a)\) 中的 \(a\) 可能已经被删了，我们要用并查集找到最近的祖先。
- 注意处理边的反向情况，可以通过一些特判 / 丢进去的时候顺便压缩方向。
可以看看代码 Atcoder/problems/AGC025E.cpp · yinjinrun/code-public-2 - 码云 - 开源中国 (gitee.com)。
上面的过于繁琐！考虑更加简单的做法！
我们对于每条路径 \((u, v)\) 连一条无向边，接着考虑从叶子推到根，如果该点的度数为奇数，就让父亲和它连无向边，这样建出图来跑欧拉回路，就可以构造出方案了！大概是这样的建图会使每一条后面补充的边的两种覆盖方向的差 \(\le 1\)，于是可以满足条件。 ↩︎
AGC052D Equal LIS
给出一个 \(n\) 阶排列 \(\{P_i\}\)，你要将其分成两个子序列 \(\{a\} \{b\}\)，满足其 \(\rm LIS\) 相等。
\(n \le 2\times 10^5\)，多测。
记 \(f_i\) 表示以 \(i\) 结尾的最长上升子序列，\(L = \max\{f_i\}\)。
如果 \(2 \mid L\)，那么将令 \(a = \{i | f_i \le \frac{L}{2}\}, b = \{i | f_i > \frac{L}{2}\}\)，易知满足条件。
如果 \(2 \nmid L\)，令 \(L = 2k + 1\)，我们怎么分，两个子序列的 \(\rm LIS\) 最大至少都是 \(k +1\)，于是我们可以构造两个 \(k + 1\) 的 \(\rm LIS\)。
如果对于一个长度为 \(L\) 的 \(\rm LIS\)，存在一个不在该 \(\rm LIS\) 中的元素 \(x\)，满足一个长度为 \(k+1\) 的 \(\rm LIS\) 包含 \(x\)，那么就是有解的。
必要性是比较显然的，至于充分性，可以通过构造来说明：
令这个包含 \(x\) 的长度为 \(k +1\) 的 \(\rm LIS\) 为 \(p_1, p_2, \dots, p_{k + 1}\)，那么 \(a = \{i | f_i \neq f_{p_j}\vee (f_i = f_x \wedge i \neq x) \}, b = P / a\)，我们就会发现对于每个集合，里面 \(f_i\) 不同的个数之多为 \(k + 1\)，于是两个集合的 \(\rm LIS\) 都是 \(\le k + 1\) 的，对于 \(a\)，原来的长度为 \(L\) 的 \(\rm LIS\) 中有 \(k\) 个不能选择，长度至少是 \(k + 1\)，而对于 \(b\)，至少有一个 \(p_1, p_2, \dots, p_{k + 1}\) 在里面于是也是 \(k + 1\) 的。
可以通过树状数组处理出 \(f_i\) 以及以 \(i\) 开头的 \(\rm LIS\) 长度 \(g_i\) 完成统计。 ↩︎
AGC003E Sequential operations on Sequence
一串数，初始为 \(1\sim n\)，现在给 \(Q\) 个操作，每次操作把数组长度变为 \(q_i\)，新增的数为上一个操作后的数组的重复。问 \(Q\) 次操作后 \(1\sim n\) 每个数出现了多少次。
\(n, Q \le 10^5, q_i \le 10^{18}\)。
居然没有想到第一步/kk！只要第一步会了，之后就比较 easy 了！
如果 \(q_i \le q_{i - 1}\)，那么 \(q_{i - 1}\) 就是没有用的，于是可以直接删除！
然后 \(q\) 就是递增的了，这时一个非常优美的性质！
我们只要求出 \(cnt_i\) 表示第 \(i\) 次操作后留下的序列会对答案产生多少影响，然后一步一步往前推即可，最开始最后的 \(cnt = 1\)。
每次我们要计算当前 \(i\) 号数组对于答案的贡献为 \(t\)，那么就是 \(\left\lfloor\frac{a_i}{a_{i - 1}}\right\rfloor\) 个 \(i - 1\) 号数组，以及 \(a_i \bmod a_{i - 1}\) 个 \(i - 1\) 前面的元素，这个可以找到最后一个 \(\le a_i \bmod a_{i - 1}\)，然后递归处理，处理到初始状态就是一个前缀的答案，直接差分处理，因为每次取模大小至少会砍半，于是复杂度是 \(\mathcal O(q \log q)\) 的。 ↩︎
AGC006C Rabbit Exercise
有 $n $ 只兔子在一个数轴上，兔子为了方便起见从 \(1\) 到 \(n\) 标号，第 \(i\) 只兔子的初始坐标为 \(x_i\)。
兔子会以以下的方式在数轴上锻炼：一轮包含 \(m\) 个跳跃，第 \(j\) 个是兔子\(a[j]\) (\(2\le a[j]\le n−1\)，\(\{a\}\) 是给出的长度为 \(m\) 的数组) 跳一下，这一下从 兔子 \(a[j]− 1\) 和 兔子 \(a[j] + 1\) 中等概率的选一个（假设选了 \(x\)），那么 \(a[j]\) 号兔子 会跳到它当前坐标关于 \(x\) 的坐标的对称点。（注意，即使兔子的位置顺序变化了，但是编号仍保持不变，这里按兔子编号算）兔子会进行 \(k\) 轮跳跃，对每个兔子，请你求出它最后坐标的期望值。
\(1 \le n \le 10^5, 1 \le m \le 10^5, k \le 10^{18}\)。
之前的考试题，补一发题解。
首先，这个概率比较离谱，但是有一个非常好的性质，假设操作元素为 \(Y\)，前一个为 \(X\)，后一个为 \(Z\)，那么 \(E'(Y) = \frac{2E(X) - E(Y) + 2E(Z) - E(y)}{2} = E(X) + E(Z) - E(Y)\)，根据这个可以做到暴力 \(\mathcal O(mk)\)。
然后考虑原来期望序列的差分，我们可以发现每次是交换两个元素，于是可以直接倍增维护这个期望序列，复杂度 \(\mathcal O(n \log k)\)。
感觉题目难点在于发现期望的变化规律…… ↩︎
AGC007D Shik and Game
Shik 君在玩一个游戏。
初始时他在数轴的 \(0\) 位置，出口在 \(E\) 位置，并且数轴上还有 \(n\) 只小熊，第 \(i\) 只小熊在 \(x_i\) 位置。
Shik 君拿着 \(n\) 块糖果出发，每走一个单位长度要花费一秒。到一个小熊的位置时，他可以送给这个小熊一块糖果，这个过程不花时间。小熊收到糖果后，\(T\) 秒以后会在它所在的位置产生一个金币。
Shik 君想知道，他从出发到收集了所有金币抵达出口，最少要花费多长时间。
\(n \le 10^5\)。
AGC 也有板子题/惊讶。
首先，肯定是将整个序列划分成一段一段，每个人每次走到一段的尽头，然后回来，因此对于这个考虑 DP。
有 \(E\) 的长度一定要走，于是我们姑且不看，只计算增量，最后将答案 \(+E\)。
设 \(f(x)\) 表示只考虑前 \(x\) 的最小增量。
如果暴力就是枚举 \(y \le x\)，表示将 \(y \to x\) 都划分为一段，那么有 \(f(x) = \min_y \{f(y - 1) +\max\{T, 2\mathrm{dis}(x, y)\} \}\)，画画图不难发现是对的。
首先这个 DP 有单调性，如果后面的 \(\max\) 是 \(T\)，那么就应该选择最前面的元素，如果是 \(2\mathrm{dis}\)，那么可以直接通过前缀和处理出来。因此只要二分分界点即可进行 DP。 ↩︎
AGC007E Shik and Travel
一颗 \(n\) 个节点的二叉树，每个节点要么有两个儿子要么没有儿子，边有边权。
你从 \(1\) 号节点出发，走到一个叶子节点。然后每一天，你可以从当前点走到另一个叶子。最后回到 \(1\) 号节点，要求到过所有叶子并且每条边经过恰好两次。
每天的路费是你走过的路径上的边权和，你的公司会为你报销大部分路费，除了你旅行中所用路费最高的，行走路线是从叶子到叶子的那一天的路费。
求你自己最少要付多少路费？
\(2 \le n, a_i, v_i \le 131072\)。
好题，启发了启发式合并的变种！（只能说大概比较像了）
不难发现，肯定要二分答案，转化为判定问题。
然后每个节点有一个属性，进去这个子树的长度以及出来这个子树的长度，然后我们要考虑如何将其儿子合并，这里是没有办法贪心的，只能 DP，然后状态数是 \(\mathcal O(n^2)\) 的，比较棘手。
这个时候可以发现，如果 \((x, y),(a, b)\) 满足 \(x \le a \wedge y \le b\)，那么 \((a, b)\) 是没有用的，于是我们可以将 \((a, b)\) 删除。
加速合并可以直接双指针，然后我们发现这个时候复杂度正确了！
为什么呢？
考虑状态大小为 \(x\) 和 \(y\) 的两个点合并，那么新状态会变成 \(\min\{x, y\}\)，这个至少会将状态数目减半，初始状态 \(\mathcal O(n)\)，因此总共复杂度不会超过 \(\mathcal O(n)\)，因为合并完了要排序去重，复杂度不超过 \(\mathcal O(n \log n)\)，加上二分是 \(\mathcal O(n\log^2n)\) 的。 ↩︎
