WC2022 讲课 钱易 杂题选讲
\(~\)
已经对 WC 考试有了心理阴影了,于是先补点讲课题目。😭
咕咕咕咕 的表示还没有更新但是未来打算更的。代码可以在 这里 找到。
IOI2021 registers
咕咕咕咕
IOI2021 dungeons
咕咕咕咕
UOJ 671 诡异操作
咕咕咕咕
会口胡了,但是听说要卡常,于是先咕着。
UOJ592 新年的聚会
交互题。有一张 \(n\) 个点 \(m\) 条边的图,你可以给定一个点集,询问该点集内的点之间有没有边。
你需要猜出这张图。
\(n\le 1000, m \le 2000\),询问次数 \(\le 50000\),询问点集大小和 \(\le 10^6\)。
分治
首先有一个结论:
对于一张 \(n\) 个点 \(m\) 条边的无向图,可以将点集划分为 \(\mathcal O(\sqrt{m})\) 个独立集
证明:
- 对于度数 \(\ge \sqrt{m}\) 的点,每个点单独作为一个独立集。
- 对于度数 \(< \sqrt{m}\) 的点,设每个点所属的独立集编号为 \(t_i\)(从 \(1\) 开始),那么 \(t_i \le \sqrt{m}\)。
- 于是独立集个数就是 \(\mathcal O(\sqrt{m})\) 的。
然后我们可以考虑快速找到两个集合 \(A, B\) 之间的边:
将 \(A\) 均匀分成两个集合 \(A_1, A_2\),\(B\) 均匀分成 \(B_1, B_2\),然后判断 \(A_1 \cup B_1, A_2 \cup B_1, A_1 \cup B_2, A_2 \cup B_2\),如果当前并集并非独立集,那么就递归下去求解。
显然,整个递归树的深度是 \(\log n\) 的,于是我们用 \(\log n\) 的代价找到了一条边,于是询问复杂度就是 \(\mathcal O(m\log n)\)的。
至于点集大小之和,太复杂了,不会证明。
UOJ604 赶路
给平面上 \(n\) 个点,没有三点共线,找到一条不自交的路径。
\(n \le 2000\)
考虑分治,设 \(\mathrm{solve}(V)\) 表示 \(V\) 中第一个点作为起点,最后一个点作为终点的方案,随便找一个点画一条先,然后将集合分成两半递归下去即可。
CF1208H Red Blue Tree
咕咕咕咕
CF566C Logistical Questions
一棵 \(n\) 个节点的树,点有点权,边有边权。
两点间的距离定义为两点间边权和的 \(\frac 32\) 次方。
求这棵树的带权重心。
\(n \le 2 \times 10^5\)。
数据结构 点分治 数学
半年前,wyl 讲这个题的时候,我还是一脸懵逼,然后甚至对这个题有了心理阴影,今天(2022.1.24)感觉这个题目是如此简单!
可以枚举点,暴力计算答案,注意到普通的重心可以不断移动来确定的,所以对于这个题,我们确定重心的方法也可以直接根据导数之和移动最优点。
这样就有 \(\mathcal O(n^2)\) 做法,但是有一个优点,如果我们类似于 P4886 快递员 - 洛谷 点分治移动,那么就是 \(\mathcal O(n\log n)\) 的。
CF1083C Max Mex
给定一棵有 \(n\) 个点的树,每个节点有点权,且构成了一个 \(0~\sim~n - 1\) 的排列。
有 \(q\) 次操作,每次操作 \(1\) 为交换两个点的点权,操作 \(2\) 为查询 \(\mathrm{mex}(l)\) 值最大的 \(\mathrm{mex}(l)\) 值,其中 \(l\) 是树上的一条路径。定义一条路径 \(l\) 的 \(\mathrm{mex}\) 值 \(\mathrm{mex}(l)\) 为这条路径上最小的没有出现过的自然数。
\(n, q \le 2\times 10^5\)
数据结构 图论
考虑可以二分答案,那么要判断满足条件的点是否形成一条链即可。
于是可以放到线段树上,每个节点维护是否该区间的点构成一条链。
具体维护的时候可以维护链头链尾,pushup 的时候讨论节点在哪里即可,略有点复杂,反正我 WA 了好几发。
「JOISC 2019 Day3」穿越时空 Bitaro
在河狸国,一条路上有 \(N\) 座城市,连接城市 \(i\) 和城市 \(i + 1\) 的那段路被称为 \(i\) 号路。为了通过 \(i\) 号道路,我们必须在满足 的时刻 \(L_i \le x \le R_i - 1\) 从城市 \(i\) 或城市 \(i + 1\) 出发,在 \(x + 1\) 时刻到达另一城市。
Bitaro 获得了穿越时空的技能。每次使用这个技能,他能回到一秒前。但他不能回到前一天:也就是说,如果他在 \(0\) 时刻与 \(1\) 时刻之间使用技能,他只能回到这一天的 \(0\) 时刻。
共有 \(Q\) 组询问,每次:
- 改变 \(P_i\) 号道路的开放时间,改后 \(P_i\) 号道路在时刻 \(S_i\) 到时刻 \(T_i\) 开放通行;
- 假设时刻 \(B_i\) 他在城市 \(A_i\),然后计算在时刻 \(D_i\) Bitaro 要到达城市 \(C_i\) 的话至少需要使用多少次技能。
\(N, Q\le 3 \times 10^5\)
数据结构 线段树
比较有意思的转换:
我们发现,如果将走路情况刻画在坐标轴上,我们的路线长这样(蒯官方的图):
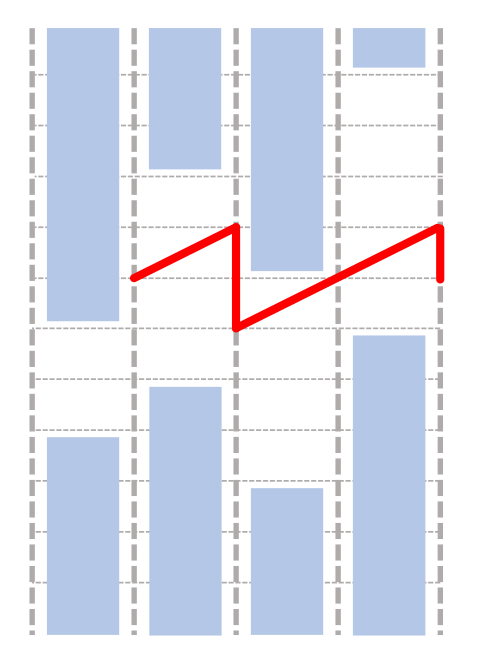
于是,我们可以平移所有区间,于是就长这样了:
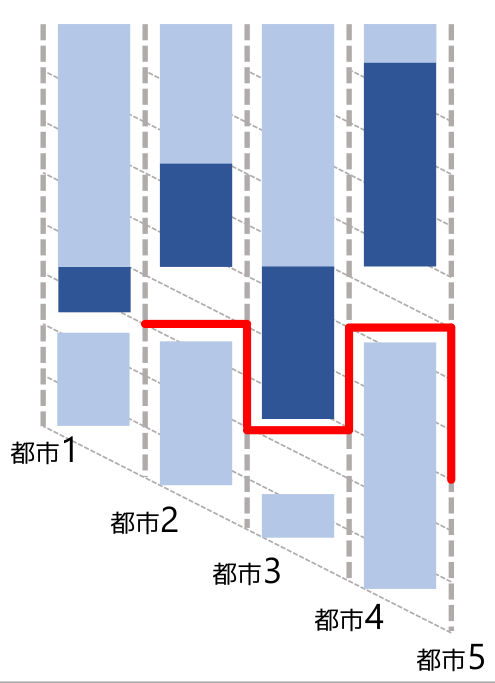
然后就转化为平移的穿越问题了。
至于有修改、查询,我们可以使用线段树维护这个过程。
对于一个区间 \([a, b]\),贡献是可以轻易算出来的,时间 \(x\) 到 \([a, b]\) 最少的穿越时间就是 \(\max\{0, x - b\}\)
我们先考虑怎么合并两个区间 \([a, b], [c, d]\):
- 如果两个区间有交,那么我们的就直接合并成了 \([a, b] \cup [c, d]\),正确性显然。
- 如果没有交集,那么我们合并之后的路径可以 \((a, b, c)\) 的形式表示出来,表示要到 \(a\) 时刻才能进入,然后出来的时间就是 \(b\),其间要穿越 \(c\) 次。
合并的时候简单讨论一下即可,具体见代码。
Gym 102979K Knowledge Is...
当初的考题,除了不输出方案以外其他都一样,印象中反悔贪心搞半天就可以做出来了。于是不更。
Gym 102586L Yosupo’s Algorithm
有红蓝两种颜色的点,每个点有个坐标 \((rx_i, ry_i)\) 或 \((bx_i, by_i)\),还有一个权值。
每次询问给定 (L, R),询问满足以下条件的点对的和的最大值,其中 \((rx_j, ry_j)\) 必须是红点,\((bx_k, by_k)\) 必须是蓝点:
- \(ry_j < by_k\)
- \((rx_j < L \wedge R < bx_k)\vee(L < rx_j \wedge bx_k < R)\)
\(1 \le n, q \le 10^5\)
数据结构 分治
首先,我们可以对于 \(y\) 进行分治,找到所有有用的点对。当我们分治 \([l, r]\) 的时候(将 \(y\in [l, mid]\) 的红点 和 \(y \in [mid + 1, r]\) 的蓝点进行配对,此时已经满足了第一个条件),如果暴力配对,那么就有 \(n^2\) 个点对了。
但是,这个限制比较有意思,如果我们用(红色点的 \(x\) 坐标,蓝色点的 \(x\) 坐标)表示一个点对,那么对于我们有用的点对 \((x, y)\) ,\(x\) 一定是 \([l, mid]\) 中红点权值最大的或者 \(y\) 一定是 \([mid+1, r]\) 中蓝点权值最大的。
因为如果 \((x, y)\) 不满足两者,而 \((A, B)\) 是满足两个条件的,考虑 \((x, y)\) 匹配的询问 \([L, R]\),那么 \(x, y\) 要么同时在 \([L, R]\) 里面或者同时在外面,而无论如何都可以将 \(x\) 换成 \(A\) 或者 \(y\) 换成 \(B\) 或者同时换并且是不劣的。
于是我们可以将分治将有用的点对个数减少到了 \(n\log n\) 级别了。
然后就是简单的二维数点问题了。
代码懒得写了。
启示
- 通过分析减少有用的点对数目,通过分治减少限制。
Luogu6580 [Ynoi2019] 美好的每一天 不连续的存在
咕咕咕咕


