题解 UVA1193 Radar Installation

原题

PDF
OJ

思路

分析

因为半径d已经确定，所以对于每个点，我们可以算出它在x 轴上的覆盖位置线段LR，如图。

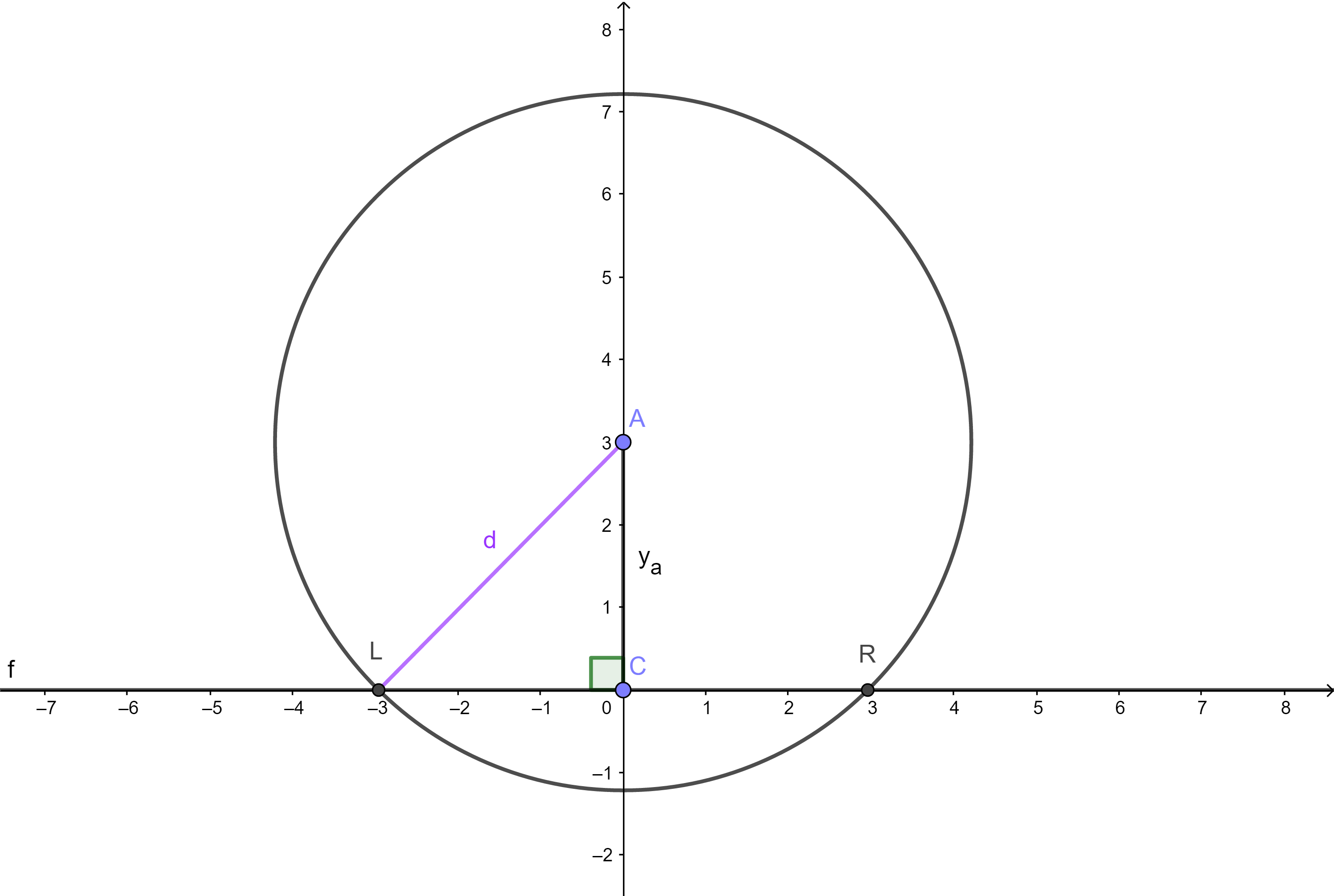
此问题便转为：

对于 n 个区间，每个区间内至少有1个点，求最少点数。

算法

我们可以将所有转化后的区间按左端点大小排序，然后记录上个点位置 las,对于每个点，有两种情况：

1. las < L , 我们必须再来一个点

2. las \(\ge\) L ,我们就可以尽量不再开点，而是使 las = \(\min\{las,R\}\) 来满足要求。

于是就可以贪心了！

代码

注意判无法达到情况。

#include <cstdio>
#include <iostream>
#include <algorithm>
#include <cmath>
#define db double
using namespace std;

const int MAXN = 1010;
int n,d,ans = 0,T = 0;
bool fail = 0;

struct island{
	int x,y;
	db l,r;
	bool operator < (const island &b) const{
		if(l == b.l) return r < b.r;
		return l < b.l;
	}
}isl[MAXN];

int main (){
	while(scanf("%d %d",&n,&d) == 2){
		if(n == 0) break;
		T++;
		fail = 0;
		ans = 1;
		if(d < 0) fail = 1; 
		double las;
		for(int i = 0;i < n;i++){
			scanf("%d %d",&isl[i].x,&isl[i].y);
			if(isl[i].y > d ) fail = 1;
			db temp = (db)( d * d - isl[i].y *isl[i].y );
			if(temp < 0){ fail = 1; continue;}
			temp = sqrt(temp);
			isl[i].l = isl[i].x - temp;
			isl[i].r = isl[i].x + temp;
		}
		printf("Case %d: ",T);
		if(fail) {
			printf("-1\n");
			continue;
		}
		sort(isl+0,isl+n);
		las = isl[0].r;
		for(int i = 1;i < n;i++){
			if(las < isl[i].l) {
				ans++;
				las = isl[i].r;
			}
			else las = min(las,isl[i].r);
		}
		printf("%d\n",ans);
	}
	return 0;
}

问题

1. 在判断不可行时：

if(isl[i].x > d ) fail = 1;

2. 在统计答案时：

if(las < isl[i].l) {
	ans++;
	las = isl[i].r;
} 
//nothing

未写

else las = min(las,isl[i].r);

这样会保留不合法情况。