数制转换，简单易懂，你学会了吗？

一、计算机的数制

• 数制：计数的方法，指用一组固定的符号和统一的规则表示数值的方法
• 数位：指数字符号在一个数中所处的位置
• 基数：指在某种进位计数制中，数位上所能使用的数字符号的个数
• 位权：指在某种进位计数制中，数位所代表的大小，即处在某一位上的“1”所表示的数值的大小

1、十进制数制系统

• 包括10个数字：0 1 2 3 4 5 6 7 8 9 0

2、十六进制数制系统

• 基数是16
• 前十个数字是0到9
• 后面是A、 B、 C、 D、 E 和F，分别表示10、11、12、13、14和15

3、数制的表示

• 十进制数（Decimal number）

（1010）₁₀ ， 1010D，1010

• 二进制数（Binary number）

（1010）₂ ,1010B

• 十六进制数（Hexadecimal number）

（1010）₁₆ ，1010H

4、数制的计算（二进制、十六进制转为十进制，采用的是上标法）

• 十进制数的特点是逢十进一

 

• 二进制数的特点是逢二进一

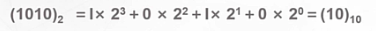
• 十六进制数的特点是逢十六进一

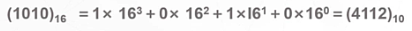
二、数制转换（十进制转为二进制、十六进制，采用是余数法）

1、十进制转为二进制，采用余数法

例如：125转为二进制

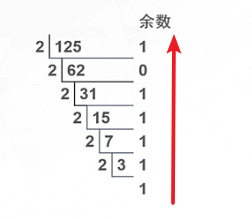
     125=1*2⁶+1*2⁵+1*2⁴+1*2³+1*2²+1*2¹+1*2⁰

     125=0111 1101B

 

2、十进制转为十六进制，依旧采用余数法

 

• 对照表

• 例如，十进制125转为十六进制

 

    125=7*16¹+13*16⁰

    125=7DH

    125=0111 1101B=7DH

3、常见的八位二进制数

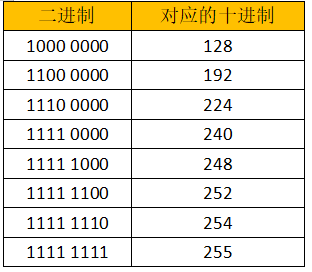
4、二进制的优点

• 二进制只需用两种状态表示数字，容易实现
• 二进制的运算规则简单

    0+0=0，0+1=1,1+0=1,1+1=0（逢二进一）

    0*0=0,  0*1=0,1*0=0,1*1=1

• 用二进制容易实现逻辑运算

       真 假

 

5、存储量

 

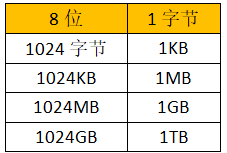
小结：二进制与十进制的转换是子网划分的基础