[ABC337G] Tree Inversion(换根 dp + 值域线段树)
题目形式就很换根 dp
如果这种题用朴素的做法求,就是暴力以每个点都做一次根跑树,自底向上统计,时间是 \(O(n^2)\)
而换根 dp 的思想就是分两步,
一般先钦定某个点(如 1)为根,统计一遍以 1 为根时的结果,
然后挖掘如果以其他点为根时,变换对结果的影响,一般就是自顶向下更新如果换根后的信息
这样分成两次 dfs,时间就是线性的 \(O(n)\)
这个题发现就是求类似树上逆序对的个数,即在同一个子树里,节点编号和深度大小关系相反
考虑第一步,设 \(f[x]\) 表示以节点编号 \(x\) 为根的子树包含逆序对个数
显然,我们要知道子树中编号小于 \(x\) 的节点数量 \(a_x\),那么转移就很显然了:
\[f[x] = a_x + \sum\limits_{y\in son(x)}f[y]
\]
考虑第二步,设 \(g[x]\) 表示以 \(x\) 为根节点的树的逆序对个数
思考由 \(x\) 换根为 \(y\) 后,\(g[x]\) 通过怎样的转换关系得到 \(g[y]\)
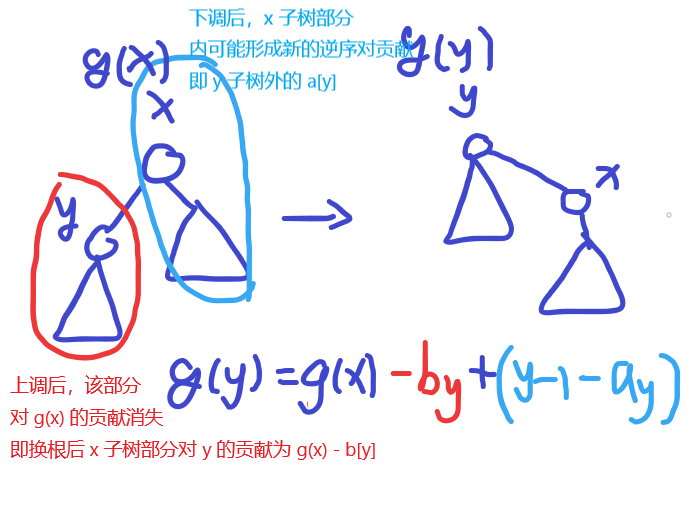
这里还需要增加一个 \(b_x\) 表示以 \(x\) 为根的子树内编号小于 \(fa[x]\) 的节点数量
需要注意的是,总的小于 \(y\) 的节点个数是 \(y - 1\),已知 \(y\) 子树内的数量有 \(a_y\),相减即子树外的部分
\[g[y] = g[x] - b_y + (y - 1 - a_y)
\]
对于 \(a_x\),\(a_y\) 的求解
也是很重要的一部分,这里是很经典的建值域线段树,或是树状数组,只不过这题是在树上
要求子树 \(x\) 内的值,可以作差一下,用全局的值减掉子树外的值即可,对应的就是递归完子树和递归子树前
时间是 \(O(n\log n)\) 的
#include <bits/stdc++.h>
#define re register int
#define lp p << 1
#define rp p << 1 | 1
#define int long long
using namespace std;
const int N = 2e5 + 10;
struct Edge
{
int to, next;
}e[N << 1];
int idx, h[N];
struct Tree
{
int l, r, sum;
}t[N << 2];
int n, f[N], g[N], a[N], b[N];
inline void add(int x, int y)
{
e[++ idx] = (Edge){y, h[x]};
h[x] = idx;
}
inline void build(int p, int l, int r)
{
t[p].l = l, t[p].r = r;
if (l == r) return;
int mid = (l + r) >> 1;
build(lp, l, mid);
build(rp, mid + 1, r);
}
inline void update(int p, int x, int k)
{
if (t[p].l == x && t[p].r == x)
{
t[p].sum += k;
return;
}
int mid = (t[p].l + t[p].r) >> 1;
if (x <= mid) update(lp, x, k);
if (x > mid) update(rp, x, k);
t[p].sum = t[lp].sum + t[rp].sum;
}
inline int query(int p, int l, int r)
{
if (l > r) return 0;
if (l <= t[p].l && t[p].r <= r) return t[p].sum;
int res = 0;
int mid = (t[p].l + t[p].r) >> 1;
if (l <= mid) res += query(lp, l, r);
if (r > mid) res += query(rp, l, r);
return res;
}
void dfs1(int u, int fa)
{
a[u] = -query(1, 1, u - 1);
b[u] = -query(1, 1, fa - 1);
for (re i = h[u]; i; i = e[i].next)
{
int v = e[i].to;
if (v == fa) continue;
dfs1(v, u);
}
update(1, u, 1);
a[u] += query(1, 1, u - 1);
b[u] += query(1, 1, fa - 1);
f[u] = a[u];
for (re i = h[u]; i; i = e[i].next)
{
int v = e[i].to;
if (v == fa) continue;
f[u] += f[v];
}
}
void dfs2(int u, int fa)
{
if (u != 1)
g[u] = g[fa] - b[u] + (u - 1 - a[u]);
for (re i = h[u]; i; i = e[i].next)
{
int v = e[i].to;
if (v == fa) continue;
dfs2(v, u);
}
}
signed main()
{
ios::sync_with_stdio(false);
cin.tie(0); cout.tie(0);
cin >> n;
for (re i = 1; i < n; i ++)
{
int x, y; cin >> x >> y;
add(x, y), add(y, x);
}
build(1, 1, n);
dfs1(1, 0);
g[1] = f[1];
dfs2(1, 0);
for (re i = 1; i <= n; i ++) cout << g[i] << ' ';
cout << '\n';
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号