2016 ACM/ICPC亚洲区青岛站现场赛（部分题解）

摘要

　　本文主要列举并求解了2016 ACM/ICPC亚洲区青岛站现场赛的部分真题，着重介绍了各个题目的解题思路，结合详细的AC代码，意在熟悉青岛赛区的出题策略，以备战2018青岛站现场赛。

 

HDU 5984 Pocky

题意

　　给出一根棒子（可以吃的）的长度x和切割过程中不能小于的长度d，每次随机的选取一个位置切开，吃掉左边的一半，对右边的棒子同样操作，直至剩余的长度不大于d时停止。现在给出x和d，问切割次数的数学期望是多少。

解题思路

　　当看到第二个样例2 1时，结果是1.693147，联想到ln(2) = 0.693147，可猜测当x > d时，答案是ln(x/d) + 1。

详细解法：

　　设长度为x、限制长度是d的棒切割次数的数学期望是f(x)，首先当x < d时，f(x) = 0（直接结束，切割次数为0）；当x >= d时，f(x) 应该是任选一点后，右边部分切割次数的数学期望加上1。设t是切割的位置，即，其中后面的式子表示切割点t的数学期望（积分0到x，取到这一点的概率乘上t的概率密度,也就是长度为t的切割次数的数学期望），进而又可以写成（积分中，系数可以自由进出），也即将f(x)写成如下形式

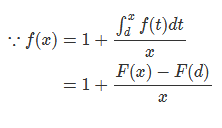
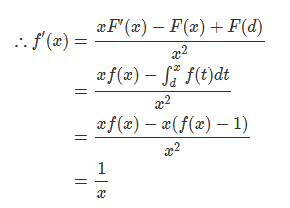
 　　由此可得f(x) = ln(x) + c，当x = d时，f(d) = ln(d) + c = 1得，c = 1 - ln(d)，代入f(x) = ln(x) - ln(d) + 1，也即f(x) = ln(x/d) + 1;

综上所述

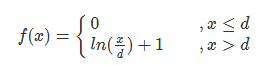
代码如下：

　　其中涉及C语言中对数的表示方法，C中只定义两log(double x)和log10(double x)，分别表示数学中的ln和lg，至于如何表示loga(b)呢？使用换底公式log(b)/log(a)即可。

 1 #include <cstdio>
 2 #include <cmath>
 3 
 4 int main()
 5 {
 6     double x, d;
 7     int T;
 8     scanf("%d", &T);
 9     while(T--) {
10         scanf("%lf%lf", &x, &d);
11         if(x <= d) 
12             printf("0.000000\n");
13         else
14             printf("%.6lf\n", log(x) - log(d) + 1);
15     }
16     return 0;
17 }

 HDU 5983 Pocket Cube

题意

　　输入一个二阶魔方的状态，问能否一步将其复原。

解题思路

　　需要细心和耐心，考虑每一种拧法，操作的时候，先顺时针改变一个面的数，然后改变四周的数，写出操作模板。要特别注意输入状态的次序，哪个面先，以及哪个角先。

代码如下：

  1 #include <cstdio>
  2 
  3 struct Magic2{
  4     int f[5], b[5], u[5], d[5], l[5], r[5];
  5     void get_u() {for(int i = 1 ; i <= 4; i++) {scanf("%d", &u[i]);}}
  6     void get_d() {for(int i = 1 ; i <= 4; i++) {scanf("%d", &d[i]);}}
  7     void get_f() {for(int i = 1 ; i <= 4; i++) {scanf("%d", &f[i]);}}
  8     void get_b() {for(int i = 1 ; i <= 4; i++) {scanf("%d", &b[i]);}}
  9     void get_l() {for(int i = 1 ; i <= 4; i++) {scanf("%d", &l[i]);}}
 10     void get_r() {for(int i = 1 ; i <= 4; i++) {scanf("%d", &r[i]);}}
 11     void L(int cnt) {
 12         for(; cnt > 0; cnt--) {
 13             int a[5];
 14             for(int i = 1; i <= 4; i++) a[i] = l[i];
 15             l[2] = a[1];l[1] = a[3];
 16             l[3] = a[4];l[4] = a[2];
 17 
 18             int x = b[3], y = b[1];
 19             b[3] = d[3], b[1] = d[1];
 20             d[3] = f[3], d[1] = f[1];
 21             f[3] = u[3], f[1] = u[1];
 22             u[3] = x, u[1] = y;
 23         }
 24     }
 25     void R(int cnt) {
 26         for(; cnt > 0; cnt--) {
 27             int a[5];
 28             for(int i = 1; i <= 4; i++) a[i] = r[i];
 29             r[1] = a[3], r[2] = a[1];
 30             r[3] = a[4], r[4] = a[2];
 31 
 32             int x = b[2], y = b[4];
 33             b[2] = u[2], b[4] = u[4];
 34             u[2] = f[2], u[4] = f[4];
 35             f[2] = d[2], f[4] = d[4];
 36             d[2] = x, d[4] = y;
 37         }
 38     }
 39     void U(int cnt) {
 40             for(; cnt > 0; cnt--) {
 41             int a[5];
 42             for(int i = 1; i <= 4; i++) a[i] = u[i];
 43             u[1] = a[3], u[2] = a[1];
 44             u[3] = a[4], u[4] = a[2];
 45 
 46             int x = b[3], y = b[4];
 47             b[3] = l[4], b[4] = l[2];
 48             l[4] = f[2], l[2] = f[1];
 49             f[2] = r[1], f[1] = r[3];
 50             r[1] = x, r[3] = y;
 51         }
 52     }
 53     void D(int cnt) {
 54         for(; cnt > 0; cnt--) {
 55             int a[5];
 56             for(int i = 1; i <= 4; i++) a[i] = d[i];
 57             d[2] = a[1], d[1] = a[3];
 58             d[4] = a[2], d[3] = a[4];
 59 
 60             int x = b[1], y = b[2];
 61             b[1] = r[4], b[2] = r[2];
 62             r[4] = f[3], r[2] = f[4];
 63             f[3] = l[1], f[4] = l[3];
 64             l[1] = x, l[3] = y;
 65         }
 66     }
 67     void F(int cnt) {
 68         for(; cnt > 0; cnt--) {
 69             int a[5];
 70             for(int i = 1; i <= 4; i++) a[i] = f[i];
 71             f[1] = a[3], f[2] = a[1];
 72             f[3] = a[4], f[4] = a[2];
 73 
 74             int x = u[3], y = u[4];
 75             u[3] = l[3], u[4] = l[4];
 76             l[3] = d[1], l[4] = d[2];
 77             d[1] = r[3], d[2] = r[4];
 78             r[3] = x, r[4] = y;
 79         }
 80     }
 81     void B(int cnt) {
 82         for(; cnt > 0; cnt--) {
 83             int a[5];
 84             for(int i = 1; i <= 4; i++) a[i] = u[i];
 85             u[1] = a[3], u[3] = a[4];
 86             u[2] = a[1], u[4] = a[2];
 87 
 88             int x = u[1], y = u[2];
 89             u[1] = r[1], u[2] = r[2];
 90             r[1] = d[4], r[2] = d[3];
 91             d[4] = l[1], d[3] = l[2];
 92             l[1] = x, l[2] = y;
 93         }
 94     }
 95     bool ok() {
 96         for(int i = 2; i <= 4; i++) {
 97             if(u[i] != u[1] || d[i] != d[1]
 98             || l[i] != l[1] || r[i] != r[1]
 99             || f[i] != f[1] || b[i] != b[1])
100                 return 0;
101         }
102         return 1;
103     }
104     bool operate(char ch) {
105         if(ch == 'u') {
106             U(1);
107             if(ok())
108                 return 1;
109             else {
110                 U(3);
111                 U(3);
112                 if(ok())
113                     return 1;
114                 else{
115                     U(1);
116                     return 0;
117                 }
118             }
119         }
120         if(ch == 'd') {
121             D(1);
122             if(ok())
123                 return 1;
124             else{
125                 D(3);
126                 D(3);
127                 if(ok())
128                     return 1;
129                 else{
130                     D(1);
131                     return 0;
132                 }
133             }
134         }
135         if(ch == 'f') {
136             F(1);
137             if(ok())
138                 return 1;
139             else{
140                 F(3);
141                 F(3);
142                 if(ok())
143                     return 1;
144                 else{
145                     F(1);
146                     return 0;
147                 }
148             }
149         }
150         if(ch == 'b') {
151             B(1);
152             if(ok())
153                 return 1;
154             else{
155                 B(3);
156                 B(3);
157                 if(ok())
158                     return 1;
159                 else{
160                     B(1);
161                     return 0;
162                 }
163             }
164         }
165         if(ch == 'l') {
166             L(1);
167             if(ok())
168                 return 1;
169             else{
170                 L(3);
171                 L(3);
172                 if(ok())
173                     return 1;
174                 else{
175                     L(1);
176                     return 0;
177                 }
178             }
179         }
180         if(ch == 'r') {
181             R(1);
182             if(ok())
183                 return 1;
184             else{
185                 R(3);
186                 R(3);
187                 if(ok())
188                     return 1;
189                 else{
190                     R(1);
191                     return 0;
192                 }
193             }
194         }
195     }
196     void print() {
197         puts("###");
198         for(int i = 1; i <= 4; i++) printf("%d ", u[i]); puts("");
199         for(int i = 1; i <= 4; i++) printf("%d ", f[i]); puts("");
200         for(int i = 1; i <= 4; i++) printf("%d ", d[i]); puts("");
201         for(int i = 1; i <= 4; i++) printf("%d ", b[i]); puts("");
202         for(int i = 1; i <= 4; i++) printf("%d ", l[i]); puts("");
203         for(int i = 1; i <= 4; i++) printf("%d ", r[i]); puts("");
204     }
205 }m2;
206 
207 int main()
208 {
209     int T;
210     scanf("%d", &T);
211     while(T--) {
212         m2.get_u();
213         m2.get_f();
214         m2.get_d();
215         m2.get_b();
216         m2.get_l();
217         m2.get_r();
218         if(m2.ok() || m2.operate('u') || m2.operate('d') || m2.operate('l')
219         || m2.operate('r') || m2.operate('f') || m2.operate('b'))
220             printf("YES\n");
221         else
222             printf("NO\n");
223     }
224     return 0;
225 }

HDU 5985 Lucky Coins

题意

　　给出n个硬币和每个硬币的数量和正面朝上的概率，问每个硬币成为幸运硬币的概率是多少。成为幸运硬币的条件是每投一次将所有背面朝上的硬币去掉，继续抛掷，直至剩下一种或者一个都剩下，那最后一种留下的硬币就是幸运硬币。

解题思路

　　概率DP，我们定义dead[i][j]表示第i种硬币在前j步以内全部被抛弃的概率，显然，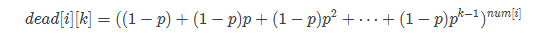

化简可得 .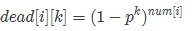

　　那么我们定义aliv[i][j] 表示第i种硬币在前j步以内至少有一个没有被抛弃的概率是 1 - dead[i][j]，那么第i个硬币成为幸运硬币的概率大概等于（应为当k = 30的时候0.5的三十次方就很小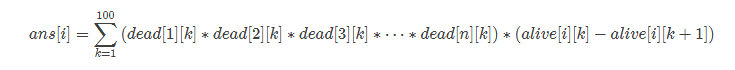），其实际意义就是第i种硬币成为幸运硬币的概率等于模拟投掷100次，而每次让第1到n种硬币在k步全部被抛弃的概率乘上第i种硬币在第k步至少还有一个而第k+1步全部被抛弃的概率，当然前面的第1到第n种硬币全部被抛弃不包括第i种硬币，故完整的式子是：

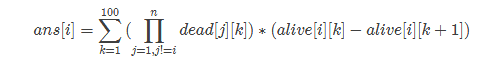
代码如下:

 1 #include <iostream>
 2 #include <cstdio>
 3 #include <cmath>
 4 #include <cstring>
 5 
 6 using namespace std;
 7 
 8 const int maxn = 15;
 9 int n;
10 double num[maxn], p[maxn], ans[maxn];
11 double dead[maxn][110], alive[maxn][110];
12 
13 void cdead() {
14     for(int k = 1; k <= 100; k++) {
15         for(int i = 0; i < n; i++) {
16             dead[i][k] = pow(1.0 - pow(p[i], k), num[i]);
17         }
18     }
19 }
20 void calive() {
21     for(int k = 1; k <= 100; k++) {
22         for(int i = 0; i < n; i++) {
23             alive[i][k] = 1.0 - dead[i][k];
24         }
25     }
26 }
27 
28 int main()
29 {
30     int T;
31     scanf("%d", &T);
32     while(T--) {
33         scanf("%d", &n);
34         for(int i = 0; i < n; i++) {
35             scanf("%lf%lf", &num[i], &p[i]);
36         }
37         if(n == 1) {
38             printf("1.000000\n");
39             continue;
40         }
41 
42         cdead();
43         calive();
44         memset(ans, 0, sizeof(ans));
45         for(int k = 1; k <= 100; k++) {
46             for(int i = 0; i < n; i++) {
47                 double tmp = 1;
48                 for(int j = 0; j < n; j++) {
49                     if(j == i)  continue;
50                     tmp *= dead[j][k];
51                 }
52                 ans[i] += tmp * (alive[i][k] - alive[i][k + 1]);
53             }
54         }
55 
56         for(int i = 0; i < n; i++) {
57             printf("%.6lf%c", ans[i], i == n - 1 ? '\n' : ' ');
58         }
59     }
60     return 0;
61 }

 　　可以看出青岛站的题目还是有难度的，主要侧重的是数学推理，准备时应该多以数学推理为主，大战在即，加油！

posted @ 2018-10-27 19:51  Reqaw  阅读(1204)  评论(0)  编辑  收藏  举报