王道数据结构——树与二叉树
本文主要讲述了数据结构中树的基本概念,二叉树,树与森林以及树与二叉树的应用。
知识框架如下图所示:
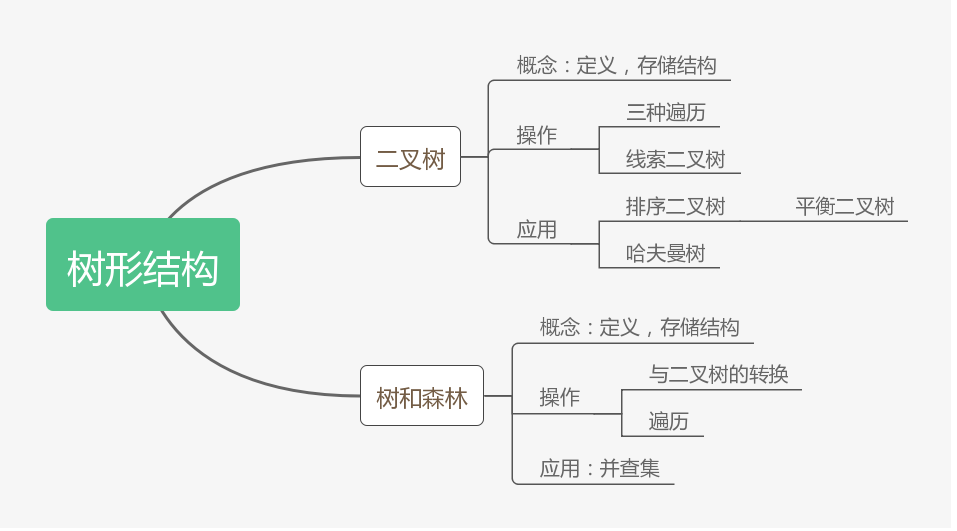
树的基本概念
树是N(N>=0)个结点的有限集合,N=0时,称为空树。
而任何一棵非空树应该满足,有且仅有一个根结点,当N>1时,其余结点又可以分为几个互不相交的有限集合,其本身又构成一个树(体现递归的定义),称为根结点的子树。需要特别说明的一个重要结论是,任何一个有N(N>=1)个结点的树都有N-1条边。
二叉树的基本概念
二叉树是一种特殊的树形结构,其特点是不存在度大于2的结点,且每个结点的子树(若有)均存在左右之分,其次序不能颠倒。
严格一点来说,二叉树是n(n>=0)个结点的有限集合。
1,n=0时,表示空二叉树。
2,n>0时,由根结点和互不相交的被称为根的左子树和右子树组成,而左子树和右子树也分别是一颗二叉树。
几种特殊的二叉树:满二叉树,完全二叉树,排序二叉树,平衡二叉树。
二叉树的存储结构
顺序存储结构,将一棵二叉树用0填充成一棵满二叉树,对于每个结点i,双亲结点为floor(i/2),左孩子为2*i,右孩子为2*i+1。
1 //二叉树的顺序存储结构 2 #define MAX_TREE_SIZE 100 3 typedef int SqBiTree[MAX_TREE_SIZE]; 4 SqBiTree bt; 5 6 //二叉树的链式存储结构 7 typedef struct BiTNode{ 8 int data; 9 struct BiTNode *lchild, *rchild; 10 }BiTNode, *BiTree;
1 #include<cstdio> 2 3 //二叉树的顺序存储结构 4 #define MAX_TREE_SIZE 100 5 typedef int SqBiTree[MAX_TREE_SIZE]; 6 SqBiTree bt; 7 8 //在顺序结构中寻找i和j的最近共同祖先 9 void Comm_Ancester(SqBiTree bt, int i, int j){ 10 int a = i, b = j; 11 if(bt[i] == 0){ 12 printf("编号为%d的结点不存在!\n", i); 13 return; 14 } 15 if(bt[j] == 0){ 16 printf("编号为%d的结点不存在!\n", j); 17 return; 18 } 19 20 while(i != j){//谁大谁往上跳一层再比,直到相等 21 if(i > j) 22 i /= 2; 23 else 24 j /= 2; 25 } 26 printf("编号为%d的结点和编号为%d的结点的最近公共祖先的结点编号为%d,其值为%d\n", a, b, i, bt[i]); 27 } 28 29 int main() 30 { 31 int bt[] = {-1, 1, 2,3, 4,5,6,7, 8,0,10,0,0,0,0,0, 0,0,0,0};//层次序列 32 /* 33 1 34 / \ 35 2 3 36 / \ / \ 37 4 5 6 7 38 / \ / \ / \ / \ 39 8 0 10 0 0 0 0 0 40 / \ / \ 41 0 0 0 0 42 */ 43 //在上述顺序存储结构中寻找编号为i和j结点的最近共同祖先结点的编号和值 44 Comm_Ancester(bt, 2, 3); 45 Comm_Ancester(bt, 4, 5); 46 Comm_Ancester(bt, 4, 6); 47 Comm_Ancester(bt, 8, 10); 48 /* 49 编号为2的结点和编号为3的结点的最近公共祖先的结点编号为1,其值为1 50 编号为4的结点和编号为5的结点的最近公共祖先的结点编号为2,其值为2 51 编号为4的结点和编号为6的结点的最近公共祖先的结点编号为1,其值为1 52 编号为8的结点和编号为10的结点的最近公共祖先的结点编号为2,其值为2 53 */ 54 55 return 0; 56 }
链式存储结构,类似定义双向链表,不同的是指向左右孩子结点
1 #include<cstdio> 2 #include<cstdlib> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 7 //二叉树的链式存储结构 8 typedef struct BiTNode{ 9 char data; 10 struct BiTNode *lchild, *rchild; 11 }BiTNode, *BiTree; 12 13 //二叉树的顺序存储结构 14 #define MaxSize 500 15 typedef struct{ 16 BiTree data[MaxSize]; 17 int front,rear; 18 } SqQueue; 19 void InitQueue(SqQueue &Q)//初始化 20 { 21 Q.front = Q.rear = 0; 22 } 23 bool QueueEmpty(SqQueue Q)//队列是否为空 24 { 25 if(Q.front == Q.rear) 26 return true;//空为真,非空为假 27 return false; 28 } 29 bool EnQueue(SqQueue &Q, BiTree x)//若队列未满,入队 30 { 31 //if(Q.rear == MaxSize) return false;//判断条件错误,可能假溢出 32 Q.data[Q.rear++] = x;//假定不会假溢出 33 return true; 34 } 35 bool DeQueue(SqQueue &Q, BiTree &x)//若队列非空,出队 36 { 37 if(Q.front == Q.rear) 38 return false; 39 x = Q.data[Q.front++]; 40 return true; 41 } 42 bool GetHead(SqQueue Q, BiTree &x)//读取队头元素,若队列非空,将队头元素赋值给x 43 { 44 if(Q.front == Q.rear) 45 return false; 46 x = Q.data[Q.front]; 47 return true; 48 } 49 void ClearQueue(SqQueue &Q)//清空队列,并回收内存 50 { 51 Q.front = Q.rear = 0; 52 } 53 54 //初始化一棵二叉树 55 void InitBiTree(BiTree &bt){ 56 bt = (BiTree)malloc(sizeof(BiTNode)); 57 } 58 //按照先根序列创建一棵二叉树 59 const char *str = "123004507006000"; 60 void CreateBiTree(BiTree &bt){ 61 //printf("%s\n", str); 62 int ch = str[0]; 63 str++; 64 if(ch == '0') 65 bt = NULL; 66 else{ 67 bt = (BiTNode*)malloc(sizeof(BiTNode)); 68 bt->data = ch; 69 CreateBiTree(bt->lchild); 70 CreateBiTree(bt->rchild); 71 } 72 } 73 //清空一棵二叉树 74 void ClearBiTree(BiTree &bt){ 75 if(bt != NULL){ 76 ClearBiTree(bt->lchild); 77 ClearBiTree(bt->lchild); 78 bt = NULL; 79 } 80 } 81 82 //判断该二叉树是否为空 83 bool BiTreeEmpty(BiTree bt){ 84 if(bt == NULL) 85 return true; 86 return false; 87 } 88 //返回该二叉树的深度 89 int BiTreeDepth(BiTree bt){ 90 if(bt != NULL){ 91 int l = 1 + BiTreeDepth(bt->lchild); 92 int r = 1 + BiTreeDepth(bt->rchild); 93 return max(l,r); 94 } 95 } 96 //先序遍历 97 void PreOrderTraverse(BiTree bt){ 98 if(bt != NULL){ 99 printf("%c", bt->data); 100 PreOrderTraverse(bt->lchild); 101 PreOrderTraverse(bt->rchild); 102 } 103 } 104 //中序遍历 105 void InOrderTraverse(BiTree bt){ 106 if(bt != NULL){ 107 InOrderTraverse(bt->lchild); 108 printf("%c", bt->data); 109 InOrderTraverse(bt->rchild); 110 } 111 } 112 //后序遍历 113 void PostOrderTraverse(BiTree bt){ 114 if(bt != NULL){ 115 PostOrderTraverse(bt->lchild); 116 PostOrderTraverse(bt->rchild); 117 printf("%c", bt->data); 118 } 119 } 120 //层次遍历 121 void levelOrderTraverse(BiTree bt){ 122 SqQueue Q; 123 InitQueue(Q); 124 BiTree p; 125 EnQueue(Q, bt); 126 while(!QueueEmpty(Q)){ 127 DeQueue(Q, p); 128 printf("%c", p->data); 129 if(p->lchild != NULL) 130 EnQueue(Q, p->lchild); 131 if(p->rchild != NULL) 132 EnQueue(Q, p->rchild); 133 } 134 } 135 136 int main() 137 { 138 /* 139 1 140 / \ 141 2 0 142 / \ 143 3 4 144 / \ / \ 145 0 0 5 6 146 / \ / \ 147 0 7 0 0 148 / \ 149 0 0 150 */ 151 //对于形如上图的二叉树 152 BiTree bt; 153 InitBiTree(bt); 154 //char str[] = "123004507006000";//先序次序,声明在前面的全局变量 155 CreateBiTree(bt); 156 PreOrderTraverse(bt);puts(""); 157 InOrderTraverse(bt);puts(""); 158 PostOrderTraverse(bt);puts(""); 159 levelOrderTraverse(bt);puts(""); 160 161 printf("该数的深度是%d\n",BiTreeDepth(bt));//计算深度并输出 162 ClearBiTree(bt); 163 if(BiTreeEmpty(bt)) 164 printf("清空成功!\n"); 165 /* 166 1234576 167 3257461 168 3756421 169 1234567 170 该数的深度是5 171 清空成功! 172 */ 173 return 0; 174 }
线索二叉树
传统的链式存储仅能体现一种父子关系,不能直接得到结点在遍历中的前驱和后继。而二叉树的链式存储结构中存在大量的空指针,若能利用这些空链域存放指向其直接前驱或后继结点的指针,则可以加快查找前驱结点和后继结点的速度。
1 #include<cstdio> 2 #include<cstdlib> 3 4 //线索二叉树的链式存储结构 5 /* 6 左前右后 7 ltag :0 lchild域指向结点的左孩子 8 :1 lchild域指向结点的前驱 9 rtag :0 rchild域指向结点的右孩子 10 :1 rchild域指向结点的后继 11 */ 12 typedef struct TreadNode{ 13 char data; 14 struct TreadNode *lchild, *rchild; 15 int ltag, rtag; 16 }ThreadNode, *ThreadTree; 17 18 void InitThreadTree(ThreadTree &bt){ 19 bt = (ThreadTree)malloc(sizeof(ThreadNode)); 20 bt->lchild = bt->rchild = NULL; 21 bt->ltag = bt->rtag = 0; 22 } 23 //按照先根序列创建一棵二叉树 24 const char *str = "12040035000"; 25 void CreateThreadTree(ThreadTree &bt){ 26 //printf("%s\n", str); 27 int ch = str[0]; 28 str++; 29 if(ch == '0') 30 bt = NULL; 31 else{ 32 bt = (ThreadNode*)malloc(sizeof(ThreadNode)); 33 bt->data = ch; 34 bt->lchild = bt->rchild = NULL; 35 bt->ltag = bt->rtag = 0; 36 CreateThreadTree(bt->lchild); 37 CreateThreadTree(bt->rchild); 38 } 39 } 40 41 /*线索二叉树的构造,即二叉树的线索化,实质上就是遍历一遍二叉树, 42 发现该结点的左右指针域是否为空,若为空,分别将其改造成指向前驱和后继结点即可, 43 不要忘记改变标志位的状态*/ 44 void InThread(ThreadTree &p, ThreadTree &pre){ 45 if(p != NULL){ 46 InThread(p->lchild, pre);//线索化左子树 47 48 if(p->lchild == NULL){ 49 p->lchild = pre; 50 p->ltag = 1; 51 } 52 if(pre != NULL && pre->rchild == NULL){ 53 pre->rchild = p; 54 pre->rtag = 1; 55 } 56 pre = p;//标记当前结点位刚刚访问过的结点 57 InThread(p->rchild, pre);//递归线索化右子树 58 } 59 } 60 //通过中序遍历建立中序线索二叉树的主过程如下 61 void CreateInThread(ThreadTree &T){ 62 ThreadTree pre = NULL; 63 //借助一个pre指针指向中序遍历时上一个刚刚访问过的结点,表示各节点的前后关系 64 if(T != NULL){ 65 InThread(T, pre); 66 pre->rchild = NULL;//处理遍历的最后一个结点 67 pre->rtag = 1; 68 } 69 } 70 //二叉树的中序遍历算法 71 void InOrderTraverse(ThreadTree bt){ 72 if(bt != NULL){ 73 InOrderTraverse(bt->lchild); 74 printf("%c", bt->data); 75 InOrderTraverse(bt->rchild); 76 } 77 } 78 //求中序线索二叉树中中序序列下的第一个结点 79 ThreadNode* Firstnode(ThreadNode *p){ 80 while(p->ltag == 0)//记得创建结点时,tag初始化为0,不然找不到中序第一个结点 81 p = p->lchild;//最左下结点(不一定是叶子结点) 82 83 return p; 84 } 85 //求中序线索二叉树中结点p在中序序列下的后继结点 86 ThreadNode* Nextnode(ThreadNode *p){ 87 if(p->rtag == 0) return Firstnode(p->rchild);//rtag == 0,右孩子存在,返回其右子树的第一个结点 88 else return p->rchild;//rtag == 1,直接返回其右孩子指针指向的后继结点 89 } 90 //不含头结点的中序线索二叉树的中序遍历算法 91 void Inorder(ThreadNode *T){ 92 for(ThreadNode *p = Firstnode(T); p != NULL; p = Nextnode(p)) 93 printf("%c", p->data);//记得创建结点时,tag初始化为0,不然找不到中序第一个结点 94 } 95 int main() 96 { 97 /* 98 1 99 / \ 100 2 3 101 / \ / \ 102 0 4 5 0 103 / \ / \ 104 0 0 0 0 105 */ 106 //对于形如上图的二叉树线索化 107 ThreadTree bt; 108 InitThreadTree(bt); 109 //char str[] = "12040035000";//先序次序,声明在前面的全局变量 110 CreateThreadTree(bt); 111 puts("二叉树中序遍历:"); 112 InOrderTraverse(bt);puts(""); 113 114 CreateInThread(bt); 115 puts("线索二叉树中序遍历:"); 116 Inorder(bt);puts(""); 117 /* 118 二叉树中序遍历: 119 24153 120 线索二叉树中序遍历: 121 24153 122 */ 123 return 0; 124 }
树的存储结构
双亲表示法
1 #include<cstdio> 2 #include<cstring> 3 //树的双亲表示法 4 #define MAX_TREE_SIZE 100 5 typedef struct{ 6 char data; 7 int parent; 8 }PTNode; 9 typedef struct{ 10 PTNode nodes[MAX_TREE_SIZE]; 11 int n = 0; 12 }PTree; 13 14 int main() 15 { 16 /* 17 对于如下的二叉树 18 0 19 1 2 3 20 4 5 6 21 7 8 9 22 */ 23 PTree pt; 24 int e[20][2]={0,-1, 1,0,2,0,3,0, 4,1,5,1, 6,3,7,6,8,6,9,6}; 25 for(int i = 0; i < 10; i++){ 26 pt.nodes[i].data = e[i][0]; 27 pt.nodes[i].parent = e[i][1]; 28 pt.n++; 29 } 30 return 0; 31 }
孩子表示法
1 /*树的孩子表示法 2 每个结点的孩子结点都用一个单链表存储其孩子结点,则N个结点就有N个单链表 3 */ 4 #define MAX_TREE_SIZE 100 5 typedef struct CTNode{//孩子结点 6 int child; 7 struct CTNode *next; 8 }*ChildPtr; 9 typedef struct{ 10 char data; 11 ChildPtr firstchild;//孩子链表头指针 12 }CTBox; 13 typedef struct{ 14 CTBox nodes[MAX_TREE_SIZE]; 15 int n, r;//结点数和根的位置 16 }CTree;
左孩子右兄弟表示法
1 /*树的左孩子右兄弟表示法 2 类似二叉树的链式存储结构,最大的优点时实现树转化为二叉树的操作,易于查找孩子结点,缺点是不利于查找双亲结点, 3 可以使用添加parent域指向其父结点的方法解决 4 */ 5 typedef struct CSNode{ 6 char data; 7 struct CSNode *firstchild, *nextsibling; 8 }CSNode, *CSTree;
欢迎交流,共同进步——



