P9901 『PG2』弯曲半平面直线同向图最大流 题解
思路
正解想不出,只好用网络流了
网络流简介请戳这儿。这道题数据有点大用 EK 求最大流似乎过不了,所以本蒟蒻采用 Dinic 算法。
Dinic 算法
Dinic 算法相当于 EK 的优化。在原基础找增广路的基础上添加了一个分层操作,再通过深搜找阻塞流。
分层
从原点开始我们把可以通过一步到达的点记作第一层,两步到达的点记作第二层,依次类推,(注:在分层途中我们不考虑每条边的长度,即将边权看作为零)。
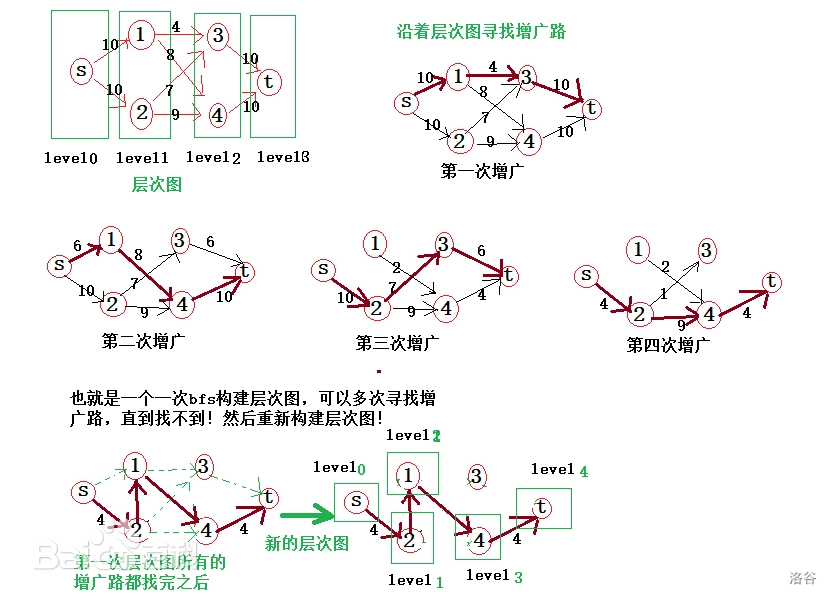
优化
在 Dinic 中有一个经典优化叫弧优化,意思是如果我们知道一条边已经增广到极限了,即已经发挥出最大价值,我们就不再用他了。
code
#include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 10005;
int n, m, s, t;
struct edge {int v, nxt, val;} e[N * 2];
int head[N], cnt = 1;
int dis[N];
int cur[N];//弧优化数组
int maxflow;
void add(int u, int v, int val) {
e[++cnt].val=val;
e[cnt].v=v;
e[cnt].nxt=head[u];
head[u] = cnt;
e[++cnt].val=0;
e[cnt].v=u;
e[cnt].nxt=head[v];
head[v] = cnt;
}
bool bfs() {
queue<int>q;
for(int i=1;i<=n;i++){
dis[i]=-1;
cur[i]=head[i];
}
q.push(s);
dis[s] = 1;
while (!q.empty()) {
int x = q.front();
q.pop();
for (int i = head[x]; i; i = e[i].nxt) {
int v = e[i].v;
if (dis[v] == -1 && e[i].val) {
q.push(v);
dis[v] = dis[x] + 1;
}
}
}
return dis[t] != -1;
}
int dfs(int u, int flow) {
if (u == t) return flow;
int res = 0;
for (int i = cur[u]; i; i = e[i].nxt) {
cur[u]=i;
int v = e[i].v;
if (dis[v] == dis[u] + 1 && e[i].val) {
int fl = dfs(v, min(e[i].val, flow));
if (fl) {
e[i].val -= fl;
e[i ^ 1].val += fl;
flow -= fl;
res += fl;
if (!flow) return res;
}
}
}
return res;
}
signed main() {
scanf("%lld%lld%lld%lld", &n, &m, &s, &t);
for (int i = 1; i <= m; ++i) {
int x, y, val;
scanf("%lld%lld%lld", &x, &y, &val);
add(x, y, val);
}
while (bfs()) maxflow += dfs(s, 1 << 29);
cout << maxflow;
return 0;
}
恭喜你获得 \(80\) 分代码,因为这道题数据过大所以需要加快读。
inline void read(register int &a)//快读模板
{
a=0;char c;
while((c=getchar())<48);
do a=(a<<3)+(a<<1)+(c^48);
while((c=getchar())>47);
}
本文来自博客园,作者:Arthur_Douglas,转载请注明原文链接:https://www.cnblogs.com/wenzhihao2023/p/18029873


