P9779_[HUSTFC 2023] 不定项选择题_题解

rt

题目

有一道共 n 个选项的不定项选择题，它的答案至少包含一个选项，由于题目与选项的内容晦涩难懂，你打算通过尝试每一种可能的答案来通过这道题。

初始时所有选项都没有被勾选，你可以执行任意次下述操作：

• 勾选一个当前未被勾选的选项。

• 取消勾选一个当前已被勾选的选项。

当你勾选中的选项与答案一致时，你将会立即通过此题。在开始尝试前，你产生了一个疑问：在最坏的情况下，至少需要操作多少次才可以通过这道题？

思路

题目描述里说的是最坏情况的最少操作,最坏情况就是最后一个一定是正确的

so

简单概括一下这道题相当于是求 n 个空需要进行几次操作到第 n 个空

用数学思路来画个图，假设 n 是三；

解：如图

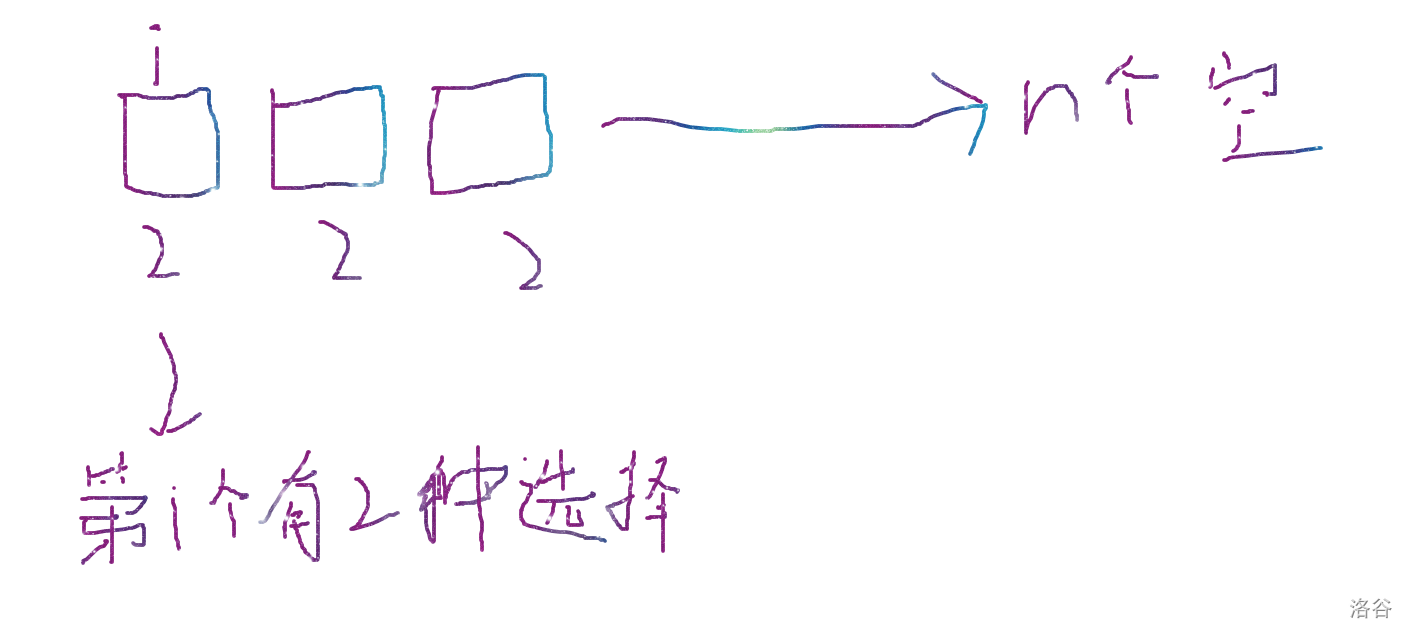
可是这里算出来共可以进行 8 次操作，因为最后一个必然正确，所以不需要进行取消勾选，最后答案要减一。算出来得7

继续简化题目

根据上面的推理这道题就简单了，答案 = 2 的 n 次幂 -1

代码

#include<bits/stdc++.h>
using namespace std;
long long n;
int main()
{
	cin>>n;
	cout<<(int)pow(2,n)-1;//pow是求幂的函数，为防止出现小数这里需要强转int
	return 0;
} 

这是本人第一篇题解，有错误请指正，谢谢

食用快乐