扩展域并查集详解

如有错漏之处，敬请各位奆佬指正！

---

这是个比较冷门的数据结构。。。（其实很简单而且并不冷门）

我是在做 P1892 [BOI2003]团伙的时候听说的。

那么，我就来讲解一下这个结构。

upd at 2020-09-17 准备开始扩写这篇文章

---

一、预备知识

• 并查集
• 好像也没了...

所以我说他很菜嘛...

二、引入

咱们做并查集的问题，基本上题面都是这样“三步走”：

1. n 个点，m 个关系（边）。
2. 给你这些关系，每个链接两点 x , y 。
3. 求两点之间是否连通。

当然第三步可能会有一些变更，例如

• 判断整个图的连通性
• 统计连通块个数

这些都可以通过一些小优化在 O(1) 的时间内完成处理。

假如在第二步上做一些变更呢？

给定两种关系。第一种：给定一对朋友关系；第二种，给定一对敌人关系，满足敌人的敌人就是朋友。

那么传统并查集就捉襟见肘了。

我们当然可以使用暴力方法（Floyd）在 O(n3) 的时间内把敌人关系预处理成朋友关系。但是这对于题目 n≤1000 的数据量来说是会 T 的。

其实有一种方法能在 O⁡(1) 的时间内优化他。那就是...

三、反集

反集的思路是再构造一个集合（称之为反集），然后将“敌人”关系通过原集和反集表示出来。

比如假设有 3 个元素 1，2，3。我们称他们的反集元素分别为 1′，2′，3′。（如下图）

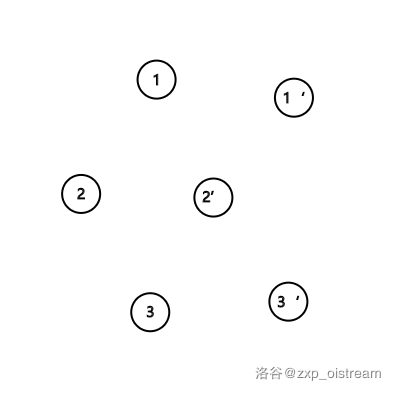
那么，如何体现敌人关系呢？

假如有一对敌人关系 (1,2)。

我们只需要连接两条边 <1,2′>，<2,1′> 就行了。

这样，在 1，2 之间构成了一个 × 形，由于 1′ 和 2′ 不会相连，所以这在并查集中也就意味着，这两个结点不会连到一起了。（如下图）

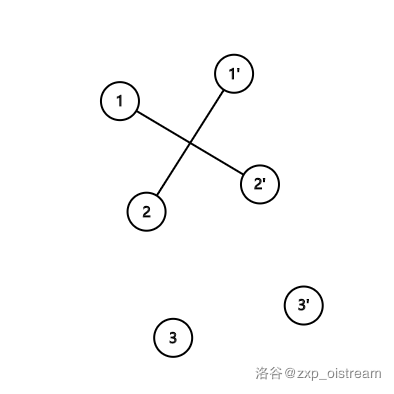
等等！还有一个敌人的敌人就是朋友关系，在这里是否是正确的呢？

假如还有一对敌人关系 (2,3)，那么，根据规则，1 与 3应该是朋友关系（在一个集合中）。

我们按照上面的规则，连接 <2,3′> 和 <3,2′>，则图变成了这样：

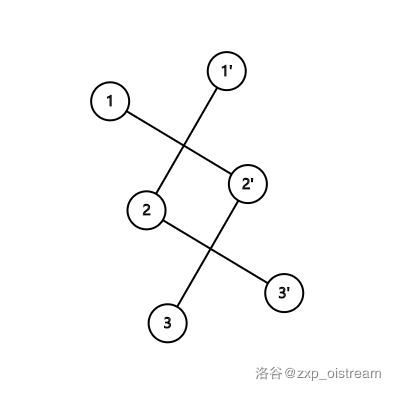
则图变成了两个连通块（如下图，红色，蓝色）。

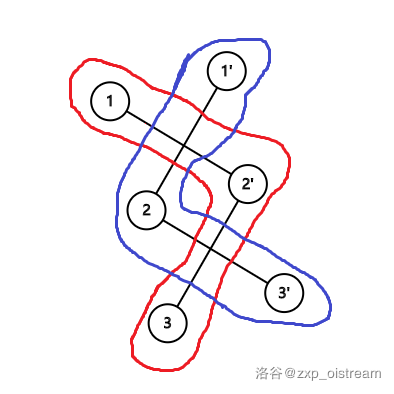
自然地，1，3 在一个连通块中了。

三、实现

在代码中，我们可以开 2×n 的数组，利用 i+n(0<i≤n) 来代替上面的 i′。

代码只需要在并查集的基础上加两个部分即可。

定义：

• ri​：并查集数组，代表第 i 个元素的代表元素。

初始化

for(int i=1;i<=2*n;i++)//注意这里的2*n。
{
    r[i]=i;
}

 

反集操作

读入结点u，v之间的关系;
if(朋友关系)
{
    union(u,v);
}
else//敌人关系。
{
    //刚刚讲过的操作。
    union(u,v+n);
    union(v,u+n);
}