| 项目 | 内容 |
|---|---|
| 课程班级博客链接 | https://edu.cnblogs.com/campus/xbsf/2018CST |
| 这个作业要求链接 | https://www.cnblogs.com/nwnu-daizh/p/14483282.htm |
| 我的课程学习目标 | (1)了解和掌握PSP流程 (2)完成项目开发并且将软件项目存入Github托管仓库 (3)再次复习{0-1}背包问题,运用编程语言完成任务3 (4)认真完成本次个人项目开发 |
| 这个作业在哪些方面帮助我实现学习目标 | (1)通过使用PSP流程,对实验时间有很好的时间把握 (2)通过首次使用Github对网站加深认识,清楚网站功能以及对git也有初步了解 |
| 项目Github的仓库链接地址 | https://github.com/xwt721/SoftwareProject/blob/23f7511db49e50d61cbe71f47395dc05f2014356/D{0-1}KP |
任务1:点评班级博客中已提交的作业
| 已被评论博客姓名 | 评论内容 | 被评论人博客地址 |
|---|---|---|
| 谢林江 | 优点: 1.页面整洁,既有图片又有文字 2.软件方面的介绍相对完整 缺点: 1.对各个软件没有比较,可以写对软件功能的比较,对使用方法的比较等等 2.个人建议使用表格可能会更能突出重点,文字部分希望简洁 |
https://www.cnblogs.com/krypton052/p/14551169.html |
| 冯永萍 | 优点: 1.博客内容相当的完整 2.各个软件的介绍很详细 缺点: 1.字体大小 2.博客内容只有文字,图片太少 建议: 1.适量的加入表格,可能会突出重点 2.可以分成各个标题,可以让博客内容中的标题更醒悟 |
https://www.cnblogs.com/fengyongping/p/14548211.html |
| 包凤梅 | 优点: 1.内容完整,对软件介绍较为完整 2.任务标题较为清晰 3.对重点的把控也很好,懂得什么时候用链接,什么时候用超链接 缺点: 1.可以把排版做的更好 2.字体大小可以稍微改变一下 3.对每个软件的认识有差距,有些深刻,有些还停留在表面 |
https://www.cnblogs.com/baofengmei/p/14544245.html |
任务2:掌握PSP流程
邹欣老师在《构建之法》中提出,软件开发的工作量和质量怎么衡量呢?给出PSP认为答案:
项目/任务有多大?
说明项目的大小, 一般用代码行数 (Line Of Code, LOC) 来表示;也可以用功能点 (function point)。 一个重要的指标是: 你在实际产品中写了多少代码, 不包括空行/注释行/单字符行
花了多少时间?
可以用小时, 天,月,年来表示。一组人所花费的时间可以用 (人数*时间) 来表示,例如某项目花费了10个人·月。
质量如何?
交付的代码中有多少缺陷? 交付有两个定义
在 Code Complete “代码完成” 的时候, 交付给测试人员
交付到顾客那里去 (在软件交付的时候)。
可以用缺陷的数量来除以项目的大小。 例如 5 bugs / KLOC, 意味着每千行程序有5个缺陷。
是否按时交付?
软件/任务是否按时交付?这个看似简单, 其实也有讲究。例如, 当我们衡量一个程序员在一段时间内的交付情况时, 我们是用简单的平均值呢, 还是用方差来表示?
-- 引用构建之法第二章
个人PSP管理
| 任务内容 | 计划共完成的时间(min) | 实际完成时间(min) |
|---|---|---|
| 计划 | 20 | 40 |
| 编制个人PSP | 10 | 8 |
| 查阅资料 | 20 | 32 |
| 开发(预计三天完成) | 390 | 610 |
| 复习两个算法(回溯法、动态规划法) | 60 | 90 |
| 复习背包问题求解方法 | 60 | 40 |
| 设计代码 | 30 | 180 |
| 编写代码 | 120 | 150 |
| 复审 | 60 | 60 |
| -- 查阅资料修改代码 | 60 | 90 |
| 报告 | 95 | 210 |
| -- 编写博客 | 60 | 90 |
| -- 提交代码 | 20 | 90 |
| -- 反思及总结 | 15 | 30 |
我在编写PSP文档时发现,计划完成学业的时间一般情况都比实际完成需要的时间久,尤其是在编写代码的过程中会出现无法预料的事情发生。起初我把设计代码部分想的过于简单,认为在编写代码时才会运用更多的时间。但是在实际情况中,设计代码这一步骤花费的时间更久,因为遇到问题我当时会去解决,担心会忘记。虽然编写代码的语言用的是python语言,但是其中的一些知识也是在当时一边学习一边完成,由于在前期对于两种算法没有很好的复习,花费的时间不够,导致后面花费的时间较多。
任务3:项目开发
开发背景
背包问题(Knapsack Problem,KP)是NP Complete问题,也是一个经典的组合优化问题,有着广泛而重要的应用背景。{0-1}背包问题({0-1}Knapsack Problem,{0-1}KP)是最基本的KP问题形式,它的一般描述为:从若干具有价值系数与重量系数的物品(或项)中,选择若干个装入一个具有载重限制的背包,如何选择才能使装入物品的重量系数之和在不超过背包载重前提下价值系数之和达到最大?
D{0-1}KP是经典{0-1}背包问题的一个拓展形式,用以对实际商业活动中折扣销售、捆绑销售等现象进行最优化求解,达到获利最大化。D{0-1}KP数据集由一组项集组成,每个项集有3项物品可供背包装入选择,其中第三项价值是前两项之和,第三项的重量小于其他两项之和,算法求解过程中,如果选择了某个项集,则需要确定选择项集的哪个物品,每个项集的三个项中至多有一个可以被选择装入背包,D{0-1} KP问题要求计算在不超过背包载重量C的条件下,从给定的一组项集中选择满足要求装入背包的项,使得装入背包所有项的价值系数之和达到最大;D{0-1}KP instances数据集是研究 D{0-1}背包问题时,用于评测和观察设计算法性能的标准数据集;动态规划算法、回溯算法是求解D{0-1}背包问题的经典算法。
参考文献
[1]肖颜,潘大志,冯世强.混合猴群算法求解折扣{0-1}背包问题[J].计算机与数字工程,2021,49(2):231-237,241. DOI:10.3969/j.issn.1672-9722.2021.02.001.
[2]吴聪聪,贺毅朝,赵建立.求解折扣{0-1}背包问题的新遗传算法[J].计算机工程与应用,2020,56(7):57-66. DOI:10.3778/j.issn.1002-8331.1904-0218.
[3]贺毅朝,王熙照,李文斌, 等.基于遗传算法求解折扣{0-1}背包问题的研究[J].计算机学报,2016,39(12):2614-2630. DOI:10.11897/SP.J.1016.2016.02614.
[4]王熙照,贺毅朝.求解背包问题的演化算法[J].软件学报,2017,28(1):1-16. DOI:10.13328/j.cnki.j0s.005139.
需求分析
当前折扣{0-1}背包问题(D{0-1}KP)模型将折扣关系作为一个新的个体,导致求解过程必需采取修复法对个体编码进行修复,求解方式较少。针对求解方法单一的问题,通过改变模型中二进制的编码表达方式,提出折扣关系不在个体编码中的表达方法。可以用布谷鸟算法求解,也可以基于细菌觅食求解折扣{0-1}背包问题。除此之外,折扣{0-1}背包问题属于一个较新的领域,在查阅了各类文献后发现最早关于折扣{0-1}背包问题是在2017年,基于此,折扣{0-1}背包问题是新时代的新问题。
功能设计
- 可正确读入实验数据文件的有效D{0-1}KP数据;
- 能够绘制任意一组D{0-1}KP数据以重量为横轴、价值为纵轴的数据散点图;
- 能够对一组D{0-1}KP数据按项集第三项的价值:重量比进行非递增排序;
- 用户能够自主选择动态规划算法、回溯算法求解指定D{0-1}KP数据的最优解和求解时间(以秒为单位);
- 任意一组D{O-1} KP数据的最优解、求解时间和解向量可保存为txt文件或导出 EXCEL文件。
程序流程图

满意代码
def DP(self): # 动态规划算法
dp = [[[0 for k in range(self.cubage + 5)] for i in range(4)] for j in range(self.size + 5)] # 三维dp数组
for k in range(1, self.size + 1):
for i in range(1, 4):
for v in range(self.cubage + 1):
for j in range(1, 4):
dp[k][i][v] = max(dp[k][i][v], dp[k - 1][j][v])
if v >= self.items[k - 1].pack[i - 1].weight:
dp[k][i][v] = max(dp[k][i][v],dp[k - 1][j][v - self.items[k - 1].pack[i - 1].weight]+self.items[k - 1].pack[i - 1].profit)
self.max_val = max(self.max_val, dp[k][i][v])
def bound(self, k, caup): # 计算上界函数,功能为剪枝
ans = self.val
while k < self.size and caup >= self.items[k].pack[2].weight:
caup -= self.items[k].pack[2].weight
ans += self.items[k].pack[2].profit
k += 1
if k < self.size:
ans += self.items[k].pack[2].profit / self.items[k].pack[2].weight * caup
return ans
def Backtracking(self, k, i, caup): # 回溯算法
bound_val = self.bound(k + 2, caup)
if k == self.size - 1:
if self.max_val < self.val:
self.max_val = self.val
self.so_res = list.copy(self.so_tmp)
return
for j in range(3):
if caup >= self.items[k + 1].pack[j].weight:
self.val += self.items[k + 1].pack[j].profit
self.so_tmp.append((k + 1, j))
self.Backtracking(k + 1, j, caup - self.items[k + 1].pack[j].weight)
self.so_tmp.pop()
self.val -= self.items[k + 1].pack[j].profit
if bound_val > self.max_val:
self.Backtracking(k + 1, j, caup)
注:由于本次项目回溯算法就算加上了剪枝时间复杂度还是指数级的,主要跟数据集的大小有关,数字越多时间成倍提升,动态规划跟数据集大小和包裹大小都相关,所以数据大部分都是动态规划才能解的,想用回溯算法,数据集大小最好在几十左右,超过一百恐怕都数以天记。
散点图
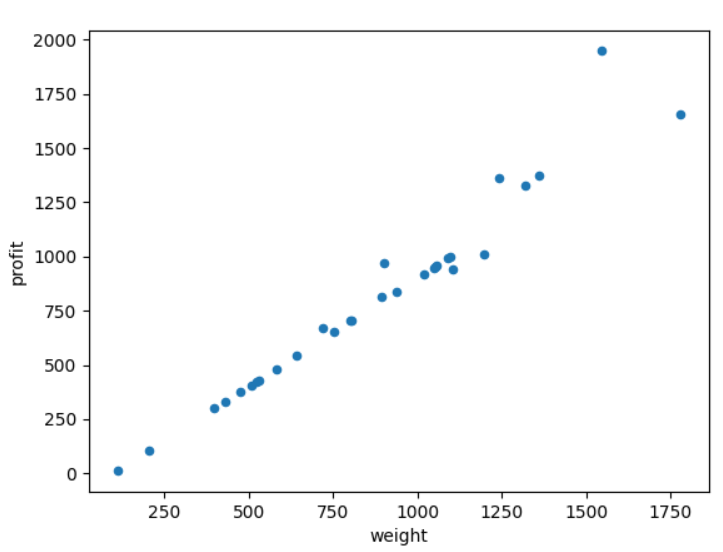
实验结果
回溯法

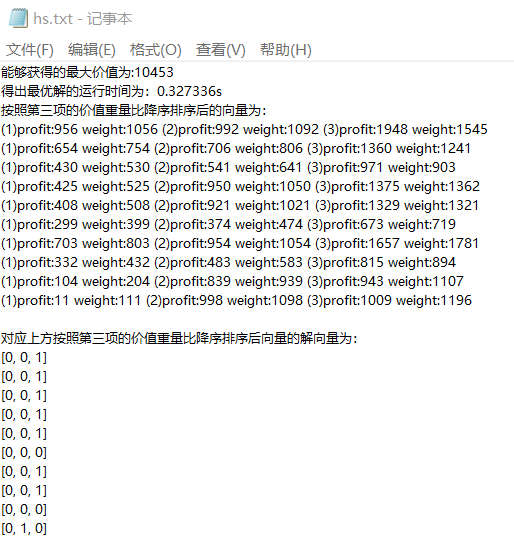
动态规划法

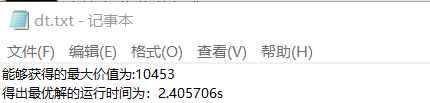
总结
通过本次实验,首先了解到了PSP设计,预计时间一般比实际时间短,造成这样结果的原因是因为对时间预测不详细、不精确,尤其是对自己的编程能力太过于自信,而且由于长时间没有接触Java、Python语言,所以在设计代码之前需要再次复习编程语言的语法以及算法结构,如何解决问题,是最重要的方面。
任务3是花费时间最多的部分,首先在查阅文献之后,对文献中的内容有初步的了解;其次,折扣{0-1}背包问题与{0-1}背包问题一定要有深刻的认识才能精确的完成代码设计;再次,运用动态规划法和回溯法解决折扣{0-1}背包问题是最亟需解决的;最后,对于折扣{0-1}背包问题的求解方法一定要精确,我花费了将近5天时间设计代码、编写代码、修改bug,真的是印象最深刻的一次实验!




