1503. Last Moment Before All Ants Fall Out of a Plank

We have a wooden plank of the length n units. Some ants are walking on the plank, each ant moves with speed 1 unit per second. Some of the ants move to the left, the other move to the right.

When two ants moving in two different directions meet at some point, they change their directions and continue moving again. Assume changing directions doesn't take any additional time.

When an ant reaches one end of the plank at a time t, it falls out of the plank imediately.

Given an integer n and two integer arrays left and right, the positions of the ants moving to the left and the right. Return the moment when the last ant(s) fall out of the plank.

 

Example 1:

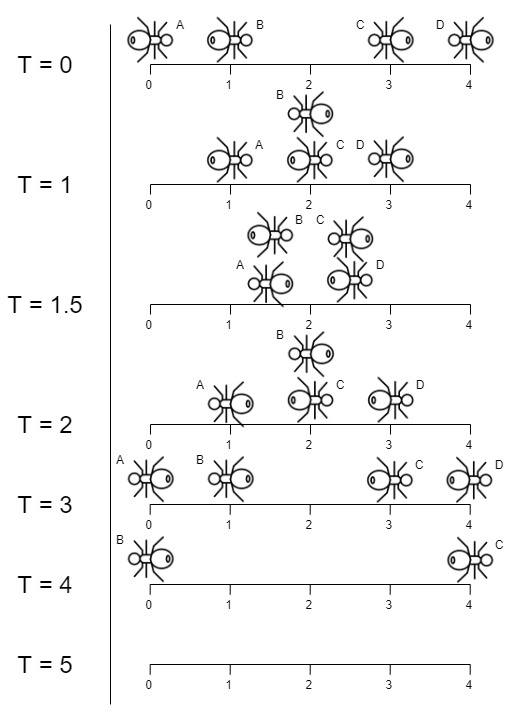
Input: n = 4, left = [4,3], right = [0,1]
Output: 4
Explanation: In the image above:
-The ant at index 0 is named A and going to the right.
-The ant at index 1 is named B and going to the right.
-The ant at index 3 is named C and going to the left.
-The ant at index 4 is named D and going to the left.
Note that the last moment when an ant was on the plank is t = 4 second, after that it falls imediately out of the plank. (i.e. We can say that at t = 4.0000000001, there is no ants on the plank).

Example 2:

Input: n = 7, left = [], right = [0,1,2,3,4,5,6,7]
Output: 7
Explanation: All ants are going to the right, the ant at index 0 needs 7 seconds to fall.

Example 3:

Input: n = 7, left = [0,1,2,3,4,5,6,7], right = []
Output: 7
Explanation: All ants are going to the left, the ant at index 7 needs 7 seconds to fall.

Example 4:

Input: n = 9, left = [5], right = [4]
Output: 5
Explanation: At t = 1 second, both ants will be at the same intial position but with different direction.

Example 5:

Input: n = 6, left = [6], right = [0]
Output: 6

先讲个笑话，有一天有个人在抹桌子，他看见桌子上有一只小蚂蚁，他就问小蚂蚁：“你的爸爸妈妈呢？”小蚂蚁回答到：“你抹死了。”.

class Solution {
    public int getLastMoment(int n, int[] left, int[] right) {
        int res = 0;
        for(int i: left){
            res = Math.max(i, res);
        }
        for(int i: right){
            res = Math.max(n - i, res);
        }
        return res;
    }
}

 

 :????  -> ???????? -> !!!!!!!!!!!!!!!!

总结：

This question is hard to use simulation way to solve, but as we go through with two test cases, we find that it doesn't matter if we know how they encounter and turn around. If two ants meet together and turn around, it's the same as they didn't turn. Brain teaser.

So what we do is to find the longest length an ant need to go. You need to count both two sides.