1462. Course Schedule IV

There are a total of n courses you have to take, labeled from 0 to n-1.

Some courses may have direct prerequisites, for example, to take course 0 you have first to take course 1, which is expressed as a pair: [1,0]

Given the total number of courses n, a list of direct prerequisite pairs and a list of queries pairs.

You should answer for each queries[i] whether the course queries[i][0] is a prerequisite of the course queries[i][1] or not.

Return a list of boolean, the answers to the given queries.

Please note that if course a is a prerequisite of course b and course b is a prerequisite of course c, then, course a is a prerequisite of course c.

 

Example 1:

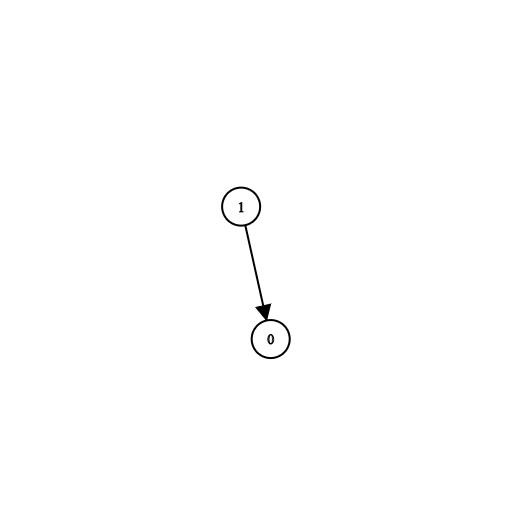
Input: n = 2, prerequisites = [[1,0]], queries = [[0,1],[1,0]]
Output: [false,true]
Explanation: course 0 is not a prerequisite of course 1 but the opposite is true.

Example 2:

Input: n = 2, prerequisites = [], queries = [[1,0],[0,1]]
Output: [false,false]
Explanation: There are no prerequisites and each course is independent.

Example 3:

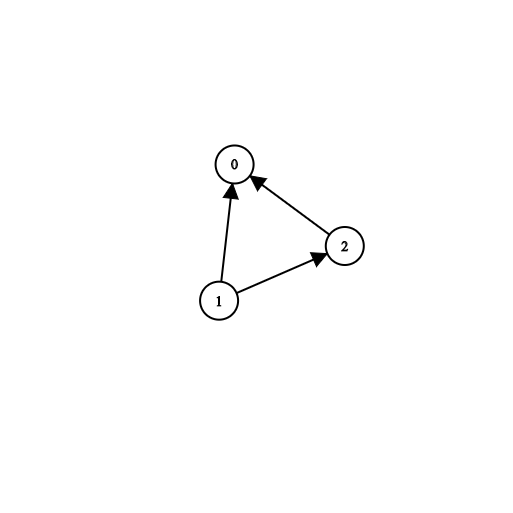
Input: n = 3, prerequisites = [[1,2],[1,0],[2,0]], queries = [[1,0],[1,2]]
Output: [true,true]

Example 4:

Input: n = 3, prerequisites = [[1,0],[2,0]], queries = [[0,1],[2,0]]
Output: [false,true]

Example 5:

Input: n = 5, prerequisites = [[0,1],[1,2],[2,3],[3,4]], queries = [[0,4],[4,0],[1,3],[3,0]]
Output: [true,false,true,false]

 

Constraints:

• 2 <= n <= 100
• 0 <= prerequisite.length <= (n * (n - 1) / 2)
• 0 <= prerequisite[i][0], prerequisite[i][1] < n
• prerequisite[i][0] != prerequisite[i][1]
• The prerequisites graph has no cycles.
• The prerequisites graph has no repeated edges.
• 1 <= queries.length <= 10^4
• queries[i][0] != queries[i][1]

class Solution {
    public List<Boolean> checkIfPrerequisite(int n, int[][] prerequisites, int[][] queries) {
        List<Boolean> res = new ArrayList();
        int[][] disto = new int[n][n];
        for(int i = 0; i < n; i++){
            Arrays.fill(disto[i], 1000);
            disto[i][i] = 0;
        }
        for(int[] arr: prerequisites){
            disto[arr[0]][arr[1]] = 1;
        }
        for (int k = 0; k < n; k++) {
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < n; j++) {
                    if (disto[i][j] > disto[i][k] + disto[k][j])
                        disto[i][j] = disto[i][k] + disto[k][j];
                }
            }
        }
        for(int i = 0; i < queries.length; i++){
            if(disto[queries[i][0]][queries[i][1]] == 1000) res.add(false);
            else res.add(true);
        }
        return res;
    }
}

floyd-walshall算法：用二维数组存放i 到 j 经过 k所需要的最小cost。

这题就按正常先把数组设置好，然后就从query里查能不能从i到j即可（等于初始值就不可以）