1314. Matrix Block Sum

Given a m * n matrix mat and an integer K, return a matrix answer where each answer[i][j] is the sum of all elements mat[r][c] for i - K <= r <= i + K, j - K <= c <= j + K, and (r, c) is a valid position in the matrix.

 

Example 1:

Input: mat = [[1,2,3],[4,5,6],[7,8,9]], K = 1
Output: [[12,21,16],[27,45,33],[24,39,28]]

Example 2:

Input: mat = [[1,2,3],[4,5,6],[7,8,9]], K = 2
Output: [[45,45,45],[45,45,45],[45,45,45]]

 

Constraints:

• m == mat.length
• n == mat[i].length
• 1 <= m, n, K <= 100
• 1 <= mat[i][j] <= 100

1.Rock大神

class Solution {
 public int[][] matrixBlockSum(int[][] mat, int K) {
        int m = mat.length, n = mat[0].length;
        int[][] rangeSum = new int[m + 1][n + 1];
        for (int i = 0; i < m; ++i)
            for (int j = 0; j < n; ++j)
                rangeSum[i + 1][j + 1] = rangeSum[i + 1][j] + rangeSum[i][j + 1] - rangeSum[i][j] + mat[i][j];
        int[][] ans = new int[m][n];
        for (int i = 0; i < m; ++i)
            for (int j = 0; j < n; ++j) {
                int r1 = Math.max(0, i - K), c1 = Math.max(0, j - K), r2 = Math.min(m, i + K + 1), c2 = Math.min(n, j + K + 1);
                ans[i][j] = rangeSum[r2][c2] - rangeSum[r2][c1] - rangeSum[r1][c2] + rangeSum[r1][c1];
            }
        return ans;
    }
}

 

 https://leetcode.com/problems/matrix-block-sum/discuss/477036/JavaPython-3-PrefixRange-sum-w-analysis-similar-to-LC-30478

2. 下面这个三哥的也可以

https://leetcode.com/problems/matrix-block-sum/discuss/477041/Java-Prefix-sum-with-Picture-explain-Clean-code-O(m*n)

class Solution {
    public int[][] matrixBlockSum(int[][] mat, int K) {
        int m = mat.length, n = mat[0].length;
        int[][] sum = new int[m + 1][n + 1]; // sum[i][j] is sum of all elements from rectangle (0,0,i,j) as left, top, right, bottom corresponding
        for (int r = 1; r <= m; r++) {
            for (int c = 1; c <= n; c++) {
                sum[r][c] = mat[r - 1][c - 1] + sum[r - 1][c] + sum[r][c - 1] - sum[r - 1][c - 1];
            }
        }
        int[][] ans = new int[m][n];
        for (int r = 0; r < m; r++) {
            for (int c = 0; c < n; c++) {
                int r1 = Math.max(0, r - K), c1 = Math.max(0, c - K);
                int r2 = Math.min(m - 1, r + K), c2 = Math.min(n - 1, c + K);
                r1++; c1++; r2++; c2++; // Since `sum` start with 1 so we need to increase r1, c1, r2, c2 by 1
                ans[r][c] = sum[r2][c2] - sum[r2][c1-1] - sum[r1-1][c2] + sum[r1-1][c1-1];
            }
        }
        return ans;
    }
}

3. 最后总结出来，此题和304一毛一样几乎

class Solution {
    private int[][] sum;
    public int[][] matrixBlockSum(int[][] mat, int K) {
        int m = mat.length, n = mat[0].length;
        sum = new int[m + 1][n + 1]; 
        for (int r = 1; r <= m; r++) {
            for (int c = 1; c <= n; c++) {
                sum[r][c] = mat[r - 1][c - 1] + sum[r - 1][c] + sum[r][c - 1] - sum[r - 1][c - 1];
            }
        }
        int[][] ans = new int[m][n];
        for (int r = 0; r < m; r++) {
            for (int c = 0; c < n; c++) {
                int r1 = Math.max(0, r - K), c1 = Math.max(0, c - K);
                int r2 = Math.min(m - 1, r + K), c2 = Math.min(n - 1, c + K);
                ans[r][c] = sumRegion(r1,c1,r2,c2);
            }
        }
        return ans;
    }
    public int sumRegion(int row1, int col1, int row2, int col2) {
    return sum[row2 + 1][col2 + 1] - sum[row2 + 1][col1]
                    - sum[row1][col2 + 1] + sum[row1][col1];
    }
}

 

第一步，得到range sum（整体的dp）

 

 

第二步，得到block sum

 为什么是这样？参考下面的图

 

 

 

 

 

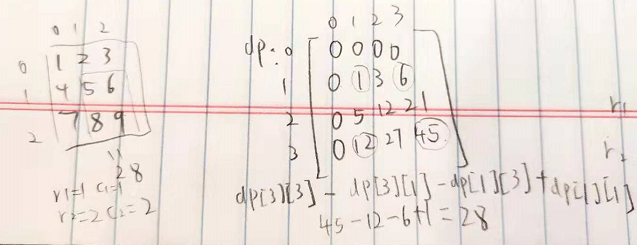
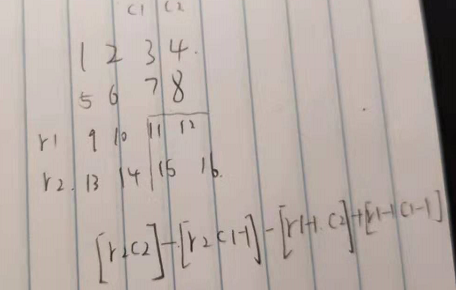
Reference：304. range sum query

一定要注意下标！！！！！！！！！！！！！！！！！！！！！！！！！

一定要注意下标！！！！！！！！！！！！！！！！！！！！！！！！！

r1, c1, r2, c2和我们要求的不一定相同（一定不相同！！！！！！！！！！！

上限和下限