1260. Shift 2D Grid

Given a 2D grid of size n * m and an integer k. You need to shift the grid k times.

In one shift operation:

• Element at grid[i][j] becomes at grid[i][j + 1].
• Element at grid[i][m - 1] becomes at grid[i + 1][0].
• Element at grid[n - 1][m - 1] becomes at grid[0][0].

Return the 2D grid after applying shift operation k times.

 

Example 1:

 

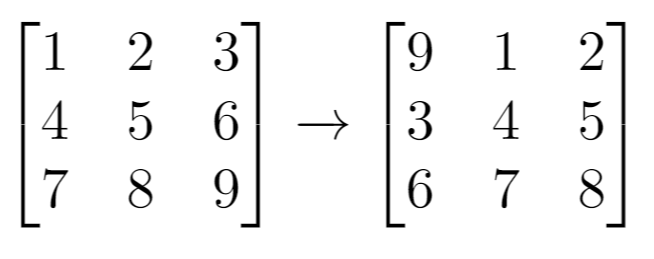
Input: grid = [[1,2,3],[4,5,6],[7,8,9]], k = 1
Output: [[9,1,2],[3,4,5],[6,7,8]]

Example 2:

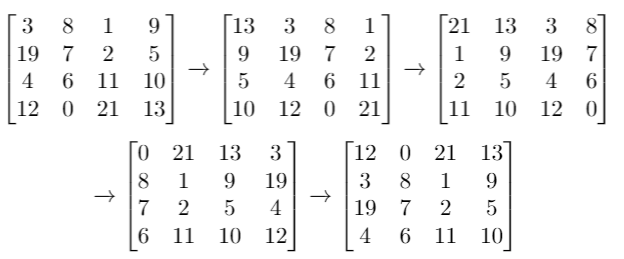
Input: grid = [[3,8,1,9],[19,7,2,5],[4,6,11,10],[12,0,21,13]], k = 4
Output: [[12,0,21,13],[3,8,1,9],[19,7,2,5],[4,6,11,10]]

Example 3:

Input: grid = [[1,2,3],[4,5,6],[7,8,9]], k = 9
Output: [[1,2,3],[4,5,6],[7,8,9]]

 

Constraints:

• 1 <= grid.length <= 50
• 1 <= grid[i].length <= 50
• -1000 <= grid[i][j] <= 1000
• 0 <= k <= 100

数学题，cnm

首先是最小化k，从原理（画个2*2）可以得到k可以优化到k % (n*m).

接下来要确定每个元素要转移到的位置，首先是column因为比较简单，算当前col（j）+ k = p，然后p < m时可以直接转换temp[i][p] = grid[i][j];

如果p>m, column就要再模m，p % m = j。

然后是比较难的row，如果p < m，就可以直接用temp[i][p] = grid[i][j]

如果p>m, 根据题意我们需要把每个第一列的元素下移，最后一个元素登顶,因为最终决定位置的是列，所以最重要加的只有(j+k) / m，最后再+row（i）模n

temp[(i + r) % n][p % m] = grid[i][j];

class Solution {
     public static List<List<Integer>> shiftGrid(int[][] grid, int k) {
            int[][] temp = new int[grid.length][grid[0].length]; // took temp grid
            int n = grid.length;
            int m = grid[0].length;
            int mod = n * m;
            k = k % mod; // minimize the k value
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < m; j++) {
                    int p = j + k; // defines which col
                    int r = p / (m); // defines which row，因为整个process是column在移动所以移动整数倍m是一样的
                    if (p < m) {
                        temp[i][p] = grid[i][j];
                    } else {
                        temp[(i + r) % n][p % m] = grid[i][j];
                    }
                }
            }
            // making temp grid into list
            List<List<Integer>> result = new LinkedList<>();
            for (int[] t : temp) {
                LinkedList<Integer> c = new LinkedList<>();
                for (int i : t) {
                    c.add(i);
                }
                result.add(c);
            }
            return result;
        }
}

 

class Solution {
     public static List<List<Integer>> shiftGrid(int[][] grid, int k) {
            int[][] temp = new int[grid.length][grid[0].length]; // took temp grid
            int n = grid.length;
            int m = grid[0].length;
            int mod = n * m;
            k = k % mod; // minimize the k value
            for (int i = 0; i < n; i++) {
                for (int j = 0; j < m; j++) {
                    int p = j + k; // defines which col
                    int r = p / m; // defines which row
                        temp[(i + r) % n][p % m] = grid[i][j]; 
                }
            }
            // making temp grid into list
            List<List<Integer>> result = new LinkedList<>();
            for (int[] t : temp) {
                LinkedList<Integer> c = new LinkedList<>();
                for (int i : t) {
                    c.add(i);
                }
                result.add(c);
            }
            return result;
        }
}