二叉树类的C++实现

　　在计算机科学中，二叉树是每个节点最多有两个子树的树结构。通常子树被称作“左子树”（left subtree）和“右子树”（right subtree）。二叉树常被用于实现二叉查找树和二叉堆。

　　二叉树的每个结点至多只有二棵子树(不存在度大于2的结点)，二叉树的子树有左右之分，次序不能颠倒。二叉树的第i层至多有个结点；深度为k的二叉树至多有个结点；对任何一棵二叉树T，如果其终端结点数为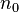，度为2的结点数为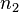，则。

　　满二叉树：一棵深度为k，且有（2的k次方）－1个节点成为满二叉树；

　　完全二叉树：深度为k，有n个节点的二叉树，当且仅当其每一个节点都深度为k的满二叉树，称之为完全二叉树；

 

　　下面是我自己实现的二叉树类，主要实现了下面的二叉树操作：

• 创建二叉树。

• 前序、中序、后续以及层次遍历二叉树。

• 求二叉树的节点数。

• 求二叉树的深度。

• 求二叉树第K层的节点个数。

• 判断两棵二叉树是否结构相同。

• 判断二叉树是不是平衡二叉树。

• 判断二叉树是不是完全二叉树。

• 求二叉树中相距最远的两个节点之间的距离。

• 求二叉树的镜像。

• 将二叉查找树变为有序的双向链表，要求不能创建新节点，只调整指针。

• 由前序遍历序列和中序遍历序列重建二叉树。

　　其中所有操作的主要思想是递归，各个函数的算法分析在源文件各个函数头注释上。 　　

 

#ifndef Tree.h

template <typename T>
struct BiNode{
    T k_data;
    BiNode<T> *LChild, *RChild;
    BiNode(T element, BiNode<T> *lt, BiNode<T> *rt):k_data(element), LChild(lt), RChild(rt){}
};

//定义树节点以及树
template <typename T>
class BiTree{
//公有函数
public:
    BiTree();
    BiTree(BiNode<T> *pRoot);
    ~BiTree();
    void GetRoot(BiNode<T> **pRoot) const;
    void VisitBiTreePreOrder(void(*Visit)(BiNode<T>)) const;
    void VisitBiTreeInOrder(void(*Visit)(BiNode<T>)) const;
    void VisitBiTreePostOrder(void(*Visit)(BiNode<T>)) const;
    int NodeCount1() const;
    int NodeCount2() const;
    int TreeDepth() const;
    void LevelTravel() const;
    void ConvertBiDirList1(BiNode<T> **pFirstNode, BiNode<T> **pLastNode);
    void ConvertBiDirList2(BiNode<T> **pFirstNode, BiNode<T> **pLastNode);
    int GetNodeNumKthLevel1(int k) const;
    int GetNodeNumKthLevel2(int k) const;
    int LeafCount() const;
    bool StructureCmp(BiNode<T> *pRoot2) const;
    bool IsBalanceBiTree() const;
    void BiTreeMirror();
    int GetMaxDistance() const;
    bool IsCompleteBinaryTree() const;
    void CreatBiTreeByPre_In(T *PreList, T *InList, int num, BiNode<T> **biNode);

//辅助函数
private:
    void CreatBiTree(BiNode<T> **pRoot);
    void ReleaseBiTree(BiNode<T> **pRoot);
    void VisitBiTreePreOrder(BiNode<T> *pRoot, void(*Visit)(BiNode<T>)) const;
    void VisitBiTreeInOrder(BiNode<T> *pRoot, void(*Visit)(BiNode<T>)) const;
    void VisitBiTreePostOrder(BiNode<T> *pRoot, void(*Visit)(BiNode<T>)) const;
    void NodeCount1(BiNode<T> *pRoot, int *count) const;
    int NodeCount2(BiNode<T> *pRoot) const;
    int TreeDepth(BiNode<T> *pRoot) const;
    void LevelTravel(BiNode<T> *pRoot) const;
    void ConvertBiDirList1(BiNode<T> *pRoot, BiNode<T> **pre);
    void ConvertBiDirList2(BiNode<T> *pRoot, BiNode<T> **pFirstNode, BiNode<T> **pLastNode);
    int GetNodeNumKthLevel2(BiNode<T> *pRoot, int k) const;
    int LeafCount(BiNode<T> *pRoot) const;
    bool StructureCmp(BiNode<T> *pRoot1, BiNode<T> *pRoot2) const;
    bool IsBalanceBiTree(BiNode<T> *pRoot, int &height) const;
    void BiTreeMirror(BiNode<T> *&pRoot);
    void GetMaxDistance(BiNode<T> *pRoot, int &Left_max, int &Right_max) const;
    bool IsCompleteBinaryTree(BiNode<T> *pRoot) const;

    BiNode<T> *root;
};

#endif

 

#include <iostream>
#include "Tree.h"
#include <queue>
#include <deque>

using namespace std;


deque<int> DequePreOrder, DequeInOrder;

template <typename T>
BiTree<T>::BiTree()
{
    CreatBiTree(&root);
}

template <typename T>
BiTree<T>::BiTree(BiNode<T> *pRoot)
{
    root = pRoot;
}

//创建二叉树
template <typename T>
void BiTree<T>::CreatBiTree(BiNode<T> **pRoot)
{
    T data;
    cin.clear();
    cin.sync();
    if(cin>>data)
    {
        *pRoot = new BiNode<T>(data, NULL, NULL);
        if (*pRoot != NULL)
        {
            CreatBiTree(&((*pRoot)->LChild));
            CreatBiTree(&((*pRoot)->RChild));
        }
        else
        {
            exit(-1);
        }
    }
    else//叶子节点
    {
        *pRoot = NULL;
    }
}

template <typename T>
BiTree<T>::~BiTree()
{
    ReleaseBiTree(&root);
}

//释放结点
template <typename T>
void BiTree<T>::ReleaseBiTree(BiNode<T> **pRoot)
{
    if (*pRoot != NULL)
    {
        ReleaseBiTree(&(*pRoot)->LChild);
        ReleaseBiTree(&(*pRoot)->RChild);
        delete (*pRoot);
    }
}

//获取根节点
template <typename T>
void BiTree<T>::GetRoot(BiNode<T> **pRoot) const
{
    *pRoot = root;
}

//打印节点
template <typename T>
void PrintNode(BiNode<T> node)
{
    cout<<node.k_data<<" ";
}

//按先序存储节点
template <typename T>
void StoreNodePreOrder(BiNode<T> node)
{
    cout<<node.k_data<<" ";
    DequePreOrder.push_back(node.k_data);//全局变量
}

//按中序存储节点
template <typename T>
void StoreNodeInOrder(BiNode<T> node)
{
    cout<<node.k_data<<" ";
    DequeInOrder.push_back(node.k_data);//全局变量
}

//遍历二叉树
template <typename T>
void BiTree<T>::VisitBiTreePreOrder(void(*Visit)(BiNode<T>)) const
{
    VisitBiTreePreOrder(root, Visit);
}

template <typename T>
void BiTree<T>::VisitBiTreePreOrder(BiNode<T> *pRoot, void(*Visit)(BiNode<T>)) const
{
    if (pRoot != NULL)
    {
        Visit(*pRoot);
        VisitBiTreePreOrder(pRoot->LChild, Visit);
        VisitBiTreePreOrder(pRoot->RChild, Visit);
    } 
}

template <typename T>
void BiTree<T>::VisitBiTreeInOrder(void(*Visit)(BiNode<T>)) const
{
    VisitBiTreeInOrder(root, Visit);
}

template <typename T>
void BiTree<T>::VisitBiTreeInOrder(BiNode<T> *pRoot, void(*Visit)(BiNode<T>)) const
{
    if (pRoot != NULL)
    {
        VisitBiTreeInOrder(pRoot->LChild, Visit);
        Visit(*pRoot);
        VisitBiTreeInOrder(pRoot->RChild, Visit);
    } 
}

template <typename T>
void BiTree<T>::VisitBiTreePostOrder(void(*Visit)(BiNode<T>)) const
{
    VisitBiTreePostOrder(root, Visit);
}

template <typename T>
void BiTree<T>::VisitBiTreePostOrder(BiNode<T> *pRoot, void(*Visit)(BiNode<T>)) const
{
    if (pRoot != NULL)
    {
        VisitBiTreePostOrder(pRoot->LChild, Visit);
        VisitBiTreePostOrder(pRoot->RChild, Visit);
        Visit(*pRoot);
    } 
}

//二叉树的结点计数。方法(1)遍历一遍即可得到。
template <typename T>
int BiTree<T>::NodeCount1() const
{
    int n = 0;
    NodeCount1(root, &n);
    return n;
}

template <typename T>
void BiTree<T>::NodeCount1(BiNode<T> *pRoot, int* count) const
{
    if (pRoot != NULL)
    {
        NodeCount1(pRoot->LChild, count);
        NodeCount1(pRoot->RChild, count);
        (*count)++;
    } 
}

//二叉树的结点计数。方法(2)如果二叉树不为空，二叉树节点个数 = 左子树节点个数 + 右子树节点个数 + 1。
template <typename T>
int BiTree<T>::NodeCount2() const
{
    return NodeCount2(root);
}

template <typename T>
int BiTree<T>::NodeCount2(BiNode<T> *pRoot) const
{
    if (pRoot != NULL)
    {
        return NodeCount2(pRoot->LChild) + NodeCount2(pRoot->RChild) + 1;
    } 
    else
    {
        return 0;
    }
}

//求二叉树的深度
template <typename T>
int BiTree<T>::TreeDepth() const
{
    return TreeDepth(root);
}

template <typename T>
int BiTree<T>::TreeDepth(BiNode<T> *pRoot) const
{
    if (pRoot != NULL)
    {
        int LDepth = TreeDepth(pRoot->LChild);
        int RDepth = TreeDepth(pRoot->RChild);
        return (LDepth>RDepth?LDepth:RDepth) + 1; 
    } 
    else
    {
        return 0;
    }
}

//分层遍历二叉树（按层次从上往下，从左往右）
template <typename T>
void BiTree<T>::LevelTravel() const
{
    LevelTravel(root);
}

template <typename T>
void BiTree<T>::LevelTravel(BiNode<T> *pRoot) const
{
    queue<BiNode<T>> q;
    if(pRoot != NULL) q.push(*pRoot);
    while(!q.empty())
    {
        BiNode<T> biNode = q.front();
        cout<<biNode.k_data<<" ";
        q.pop();
        if (biNode.LChild != NULL)
        {
            q.push(*(biNode.LChild));
        }
        if (biNode.RChild != NULL)
        {
            q.push(*(biNode.RChild));
        }
    }
}

//将二叉查找树变为有序的双向链表，要求不能创建新节点，只调整指针。方法(1)。
//pFirstNode: 转换后双向有序链表的第一个节点指针
//pLastNode: 转换后双向有序链表的最后一个节点指针
template <typename T>
void BiTree<T>::ConvertBiDirList1(BiNode<T> **pFirstNode, BiNode<T> **pLastNode)
{
    if (root == NULL)
    {
        return;
    }

    BiNode<T> *pre = NULL;
    ConvertBiDirList1(root, &pre);

    //定位头结点和尾结点
    BiNode<T> *p = root;
    while(p->LChild != NULL)
    {
        p = p->LChild;
    }
    *pFirstNode = p;

    p = root;
    while(p->RChild != NULL)
    {
        p = p->RChild;
    }
    *pLastNode = p;
}

template <typename T>
void BiTree<T>::ConvertBiDirList1(BiNode<T> *pRoot, BiNode<T> **pre)//实质为中序遍历二叉查找树，其中设置一个pre指针指向上一个节点。注意pre为引用类型。
{
    if (pRoot != NULL)
    {
        bool flag_pre = false;
        bool flag_p = false;
        ConvertBiDirList1(pRoot->LChild, pre);
        
        //线索化
        if (*pre != NULL && (*pre)->RChild == NULL) {(*pre)->RChild = pRoot; flag_pre = true;}
        if (pRoot->LChild == NULL) {pRoot->LChild = *pre; flag_p = true;}
        
        //修正与线索不一致的指针
        if(flag_pre == true && pRoot->LChild != *pre) pRoot->LChild = *pre;
        if(flag_p == true && *pre && (*pre)->RChild != pRoot) (*pre)->RChild = pRoot;

        *pre = pRoot;//更新pre

        ConvertBiDirList1(pRoot->RChild, pre);
    }
}

//将二叉查找树变为有序的双向链表，要求不能创建新节点，只调整指针。方法(2)。
//递归解法：
//（1）如果二叉树查找树为空，不需要转换，对应双向链表的第一个节点是NULL，最后一个节点是NULL
//（2）如果二叉查找树不为空：
//    如果左子树为空，对应双向有序链表的第一个节点是根节点，左边不需要其他操作；
//    如果左子树不为空，转换左子树，二叉查找树对应双向有序链表的第一个节点就是左子树转换后双向有序链表的第一个节点，同时将根节点和左子树转换后的双向有序链表的最后一个节点连接；
//    如果右子树为空，对应双向有序链表的最后一个节点是根节点，右边不需要其他操作；
//    如果右子树不为空，对应双向有序链表的最后一个节点就是右子树转换后双向有序链表的最后一个节点，同时将根节点和右子树转换后的双向有序链表的第一个节点连接。
template <typename T>
void BiTree<T>::ConvertBiDirList2(BiNode<T> **pFirstNode, BiNode<T> **pLastNode)
{
    ConvertBiDirList2(root, pFirstNode, pLastNode);
}

template <typename T>
void BiTree<T>::ConvertBiDirList2(BiNode<T> *pRoot, BiNode<T> **pFirstNode, BiNode<T> **pLastNode)
{
    if (pRoot == NULL)
    {
        *pFirstNode = NULL;
        *pLastNode = NULL;
    }
    BiNode<T> *pLeftFirst, *pLeftLast, *pRightFirst, *pRightLast;  
    if (pRoot->LChild == NULL)//处理左子树
    {
        *pFirstNode = pRoot;
    }
    else
    {
        ConvertBiDirList2(pRoot->LChild, &pLeftFirst, &pLeftLast);
        *pFirstNode = pLeftFirst;

        pLeftLast->RChild = pRoot;
        pRoot->LChild = pLeftLast;
    }

    if (pRoot->RChild == NULL)//处理右子树
    {
        *pLastNode = pRoot;
    }
    else
    {
        ConvertBiDirList2(pRoot->RChild, &pRightFirst, &pRightLast);
        *pLastNode = pRightLast;

        pRoot->RChild = pRightFirst;
        pRightFirst->LChild = pRoot;
    }
}

//求二叉树第K层的节点个数。方法(1)。
template <typename T>
int BiTree<T>::GetNodeNumKthLevel1(int k) const
{
    if (root == NULL)
    {
        return 0;
    }
    else
    {
        queue<BiNode<T>> q;
        q.push(*root);    
        while (--k)//遍历前k-1层
        {
            queue<BiNode<T>> q_NextLayer;//清空暂存队列
            while(!q.empty())//遍历其中一层
            {
                if (q.front().LChild != NULL)
                {
                    q_NextLayer.push(*(q.front().LChild));
                }

                if (q.front().RChild != NULL)
                {
                    q_NextLayer.push(*(q.front().RChild));
                }
                q.pop();
            }
            q = q_NextLayer;
        }
        return q.size();
    }
}

//求二叉树第K层的节点个数。方法(2)。
template <typename T>
int BiTree<T>::GetNodeNumKthLevel2(int k) const
{
    return GetNodeNumKthLevel2(root, k);
}

//求二叉树第K层的节点个数
//    递归解法：
//    （1）如果二叉树为空或者k<1返回0
//    （2）如果二叉树不为空并且k==1，返回1
//    （3）如果二叉树不为空且k>1，返回左子树中k-1层的节点个数与右子树k-1层节点个数之和
//    参考代码如下：
template <typename T>
int BiTree<T>::GetNodeNumKthLevel2(BiNode<T> *pRoot, int k) const
{  
    if(pRoot == NULL || k < 1)
        return 0;
    if(pRoot != NULL && k == 1)
        return 1;
    int numLeft = GetNodeNumKthLevel2(pRoot->LChild, k-1); // 左子树中k-1层的节点个数
    int numRight = GetNodeNumKthLevel2(pRoot->RChild, k-1); // 右子树中k-1层的节点个数
    return (numLeft + numRight);
}

//求二叉树中叶子节点的个数
template <typename T>
int BiTree<T>::LeafCount() const
{
    return LeafCount(root);
}

template <typename T>
int BiTree<T>::LeafCount(BiNode<T> *pRoot) const
{
    if (pRoot == NULL)
    {
        return 0;
    }
    if (pRoot->LChild == NULL && pRoot->RChild == NULL)
    {
        return 1;
    }
    return LeafCount(pRoot->LChild) + LeafCount(pRoot->RChild);
}

//判断两棵二叉树是否结构相同
//    不考虑数据内容。结构相同意味着对应的左子树和对应的右子树都结构相同。
//    递归解法：
//    （1）如果两棵二叉树都为空，返回真
//    （2）如果两棵二叉树一棵为空，另一棵不为空，返回假
//    （3）如果两棵二叉树都不为空，如果对应的左子树和右子树都同构返回真，其他返回假
template <typename T>
bool BiTree<T>::StructureCmp(BiNode<T> *pRoot2) const
{
    return StructureCmp(root, pRoot2);
}

template <typename T>
bool BiTree<T>::StructureCmp(BiNode<T> *pRoot1, BiNode<T> *pRoot2) const
{
    if (pRoot1 == NULL && pRoot2 == NULL)
    {
        return true;
    }
    if (pRoot1 == NULL && pRoot2 != NULL || pRoot1 != NULL && pRoot2 == NULL)
    {
        return false;
    }
    return StructureCmp(pRoot1->LChild, pRoot2->LChild) && StructureCmp(pRoot1->RChild, pRoot2->RChild);
}

//判断二叉树是不是平衡二叉树
template <typename T>
bool BiTree<T>::IsBalanceBiTree() const
{
    int height = 0;
    return IsBalanceBiTree(root, height);
}

template <typename T>
bool BiTree<T>::IsBalanceBiTree(BiNode<T> *pRoot, int &height) const
{
    if (pRoot == NULL)
    {    
        height = 0;
        return true;
    }
    int LHeight, RHeight;

    bool Lbal = IsBalanceBiTree(pRoot->LChild, LHeight);
    bool Rbal = IsBalanceBiTree(pRoot->RChild, RHeight);
    height = (LHeight > RHeight ? LHeight : RHeight) + 1;

    if (Lbal && Rbal && abs(LHeight - RHeight) <= 1)
    {
        return true;
    }
    return false;
}

//求二叉树的镜像
template <typename T>
void BiTree<T>::BiTreeMirror()
{
    BiTreeMirror(root);
}

template <typename T>
void BiTree<T>::BiTreeMirror(BiNode<T> *&pRoot)
{
    if (pRoot == NULL)
    {
        return;
    }

    BiNode<T> *tmp = NULL;
    tmp = pRoot->LChild;
    pRoot->LChild = pRoot->RChild;
    pRoot->RChild = tmp;

    BiTreeMirror(pRoot->LChild);
    BiTreeMirror(pRoot->RChild);
}

//求二叉树中节点的最大距离
//即二叉树中相距最远的两个节点之间的距离。先求左子树和右子树分别的最大值。
template <typename T>
int BiTree<T>::GetMaxDistance() const
{
    int Left_max, Right_max;
    GetMaxDistance(root, Left_max, Right_max);
    return Left_max + Right_max;
}

template <typename T>
void BiTree<T>::GetMaxDistance(BiNode<T> *pRoot, int &Left_max, int &Right_max) const
{
    int L_maxLeft, L_maxRight, R_maxLeft, R_maxRight;
    if (pRoot->LChild == NULL && pRoot->RChild == NULL)
    {
        Left_max = Right_max = 0;
    }
    else if (pRoot->LChild == NULL && pRoot->RChild != NULL)
    {
        Left_max = 0;

        GetMaxDistance(pRoot->RChild, R_maxLeft, R_maxRight);
        Right_max = (R_maxLeft>R_maxRight?R_maxLeft:R_maxRight) + 1;
    }
    else if (pRoot->LChild != NULL && pRoot->RChild == NULL)
    {
        GetMaxDistance(pRoot->LChild, L_maxLeft, L_maxRight);
        Left_max = (L_maxLeft>L_maxRight?L_maxLeft:L_maxRight) + 1;

        Right_max = 0;
    }
    else
    {
        GetMaxDistance(pRoot->LChild, L_maxLeft, L_maxRight);
        Left_max = (L_maxLeft>L_maxRight?L_maxLeft:L_maxRight) + 1;

        GetMaxDistance(pRoot->RChild, R_maxLeft, R_maxRight);
        Right_max = (R_maxLeft>R_maxRight?R_maxLeft:R_maxRight) + 1;
    }
}

//判断二叉树是不是完全二叉树
//若设二叉树的深度为h，除第 h 层外，其它各层 (1～h-1) 的结点数都达到最大个数，第 h 层所有的结点都连续集中在最左边，这就是完全二叉树。
//    有如下算法，按层次（从上到下，从左到右）遍历二叉树，当遇到一个节点的左子树为空时，则该节点右子树必须为空，且后面遍历的节点左右子树都必须为空，否则不是完全二叉树。
template <typename T>
bool BiTree<T>::IsCompleteBinaryTree() const
{
    return IsCompleteBinaryTree(root);
}

template <typename T>
bool BiTree<T>::IsCompleteBinaryTree(BiNode<T> *pRoot) const
{
    if (pRoot == NULL)
    {
        return true;
    }

    bool MustHasNoChild = false;
    queue<BiNode<T>> q;
    q.push(*pRoot);
    while(!q.empty())
    {
        BiNode<T> Cur = q.front();
        q.pop();
        if (MustHasNoChild)
        {
            if (Cur.LChild != NULL || Cur.RChild != NULL)
            {
                return false;
            }
        }
        else
        {
            if (Cur.LChild != NULL && Cur.RChild != NULL)
            {
                q.push(*(Cur.LChild));
                q.push(*(Cur.RChild));
            } 
            else if(Cur.LChild != NULL && Cur.RChild == NULL)
            {
                MustHasNoChild = true;
                q.push(*(Cur.LChild));
            }
            else if (Cur.LChild == NULL && Cur.RChild == NULL)
            {
                MustHasNoChild = true;
            }
            else
            {
                return false;
            }
        }
    }
    return true;
}

//由前序遍历序列和中序遍历序列重建二叉树
//    二叉树前序遍历序列中，第一个元素总是树的根节点的值。中序遍历序列中，左子树的节点的值位于根节点的值的左边，右子树的节点的值位于根节点的值的右边。
template <typename T>
void BiTree<T>::CreatBiTreeByPre_In(T* PreList, T* InList, int num, BiNode<T> **biNode)
{
    if (num <= 0)
        return; 

    if (num == 1)
    {
        *biNode = new BiNode<T>(PreList[0], NULL, NULL);
        return;
    }

    int LLen = 0;
    while(InList[LLen] != PreList[0]){LLen++;}//求前序遍历序列的第一个节点在中序遍历序列中的位置

    //左子树的前序和中序遍历
    T *LPreList = PreList + 1;
    T *LInList = InList;

    //右子树的前序和中序遍历
    T *RPreList = PreList +  LLen + 1;
    T *RInList = InList + LLen + 1;

    BiNode<T> *LChild = NULL;
    BiNode<T> *RChild = NULL;

    CreatBiTreeByPre_In(LPreList, LInList, LLen, &LChild);
    CreatBiTreeByPre_In(RPreList, RInList, num - LLen - 1, &RChild);

    *biNode = new BiNode<T>(PreList[0], LChild, RChild);
}

 

void main()
{
    BiTree<int> *p_BiTree = new BiTree<int>();
    cout<<"前序遍历：";
    p_BiTree->VisitBiTreePreOrder(PrintNode);
    cout<<endl;
    cout<<"中序遍历：";
    p_BiTree->VisitBiTreeInOrder(PrintNode);
    cout<<endl;
    cout<<"后序遍历：";
    p_BiTree->VisitBiTreePostOrder(PrintNode);
    cout<<endl;

    cout<<"节点数："<<p_BiTree->NodeCount1();
    cout<<endl;
    cout<<"节点数："<<p_BiTree->NodeCount2();
    cout<<endl;

    cout<<"深度："<<p_BiTree->TreeDepth();
    cout<<endl;

    cout<<"按层次遍历：";
    p_BiTree->LevelTravel();
    cout<<endl;

    //将二叉排序树转换为有序链表
    //BiNode<int> *pFirst = NULL;
    //BiNode<int> *pLast = NULL;
    ////p_BiTree->ConvertBiDirList1(&pFirst, &pLast);
    //p_BiTree->ConvertBiDirList2(&pFirst, &pLast);

    //BiNode<int> *p = pFirst;
    //while(p != NULL)
    //{
    //    cout<<p->k_data<<" ";p = p->RChild;
    //}
    //cout<<endl;

    //p = pLast;
    //while(p != NULL)
    //{
    //    cout<<p->k_data<<" ";p = p->LChild;
    //}

    while (0)
    {
        cout<<"请输入层数：";
        cin.clear();
        cin.sync();
        int k;
        cin>>k;
        cout<<"第"<<k<<"层结点个数为："<<p_BiTree->GetNodeNumKthLevel1(k)<<endl;
        cout<<"第"<<k<<"层结点个数为："<<p_BiTree->GetNodeNumKthLevel2(k)<<endl;
    }

    cout<<"叶子节点数为："<<p_BiTree->LeafCount()<<endl;

    while (0)
    {
        cout<<"请输入树2："<<endl;
        BiTree<int> *p_BiTree2 = new BiTree<int>();
        cout<<"前序遍历：";
        p_BiTree2->VisitBiTreePreOrder(PrintNode);
        cout<<endl;
    
        BiNode<int> *p_Node = new BiNode<int>(0, NULL, NULL);
        p_BiTree2->GetRoot(&p_Node);
        cout<<"两树结构相同吗？"<<p_BiTree->StructureCmp(p_Node)<<endl;
        delete p_Node;
        delete p_BiTree2;
    }

    cout<<"二叉树是否是平衡树："<<p_BiTree->IsBalanceBiTree()<<endl;
    cout<<"是否是完全二叉树："<<p_BiTree->IsCompleteBinaryTree()<<endl;
    cout<<"最大距离为："<<p_BiTree->GetMaxDistance()<<endl;

    //p_BiTree->BiTreeMirror();

    //cout<<"作镜像后，前序遍历：";
    //p_BiTree->VisitBiTreePreOrder(PrintNode);
    //cout<<endl;
    //cout<<"作镜像后，中序遍历：";
    //p_BiTree->VisitBiTreeInOrder(PrintNode);
    //cout<<endl;
    //cout<<"作镜像后，后序遍历：";
    //p_BiTree->VisitBiTreePostOrder(PrintNode);
    //cout<<endl;

    //cout<<"作镜像后，是否是完全二叉树："<<p_BiTree->IsCompleteBinaryTree()<<endl;

    cout<<"按前序存储节点：";
    p_BiTree->VisitBiTreePreOrder(StoreNodePreOrder);
    cout<<endl;

    cout<<"按中序存储节点：";
    p_BiTree->VisitBiTreeInOrder(StoreNodeInOrder);
    cout<<endl;

    BiNode<int> *BuildedTree = new BiNode<int>(0, NULL, NULL);
    int NodeNum = DequePreOrder.size();
    int *PreOrder = new int[NodeNum];
    for(int i = 0;i < NodeNum; i++){PreOrder[i] = DequePreOrder[i];}
    int *InOrder = new int[NodeNum];
    for(int i = 0;i < NodeNum; i++){InOrder[i] = DequeInOrder[i];}
    p_BiTree->CreatBiTreeByPre_In(PreOrder, InOrder, NodeNum, &BuildedTree);

    BiTree<int> *p_BiTree3 = new BiTree<int>(BuildedTree);

    cout<<"BuildedTree前序遍历：";
    p_BiTree3->VisitBiTreePreOrder(PrintNode);
    cout<<endl;
    cout<<"BuildedTree中序遍历：";
    p_BiTree3->VisitBiTreeInOrder(PrintNode);
    cout<<endl;
    cout<<"BuildedTree后序遍历：";
    p_BiTree3->VisitBiTreePostOrder(PrintNode);
    cout<<endl;

    delete BuildedTree;
    delete PreOrder;
    delete InOrder;

    delete p_BiTree;

    system("pause");
}