LCS最长公共子序列求解及输出所有最长公共子序列问题

子串：原序列中必须连续的一段
子序列：原序列中可以不连续的一段
注意：无论是子串和子序列，元素的顺序都是原序列中的顺序

 

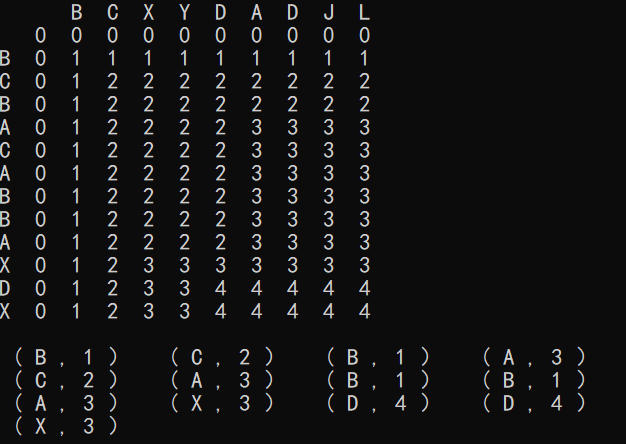
一个显而易见的事实就是当X[i] = Y[j] 的时候的所有取值中，选择最大到最长公共子序列长度的 1，2，3 。。。。N的递增子序列便是一个最长的公共子序列。

如上例所示，按顺序选取1，2，3，4的子序列对应的字符串序列就是答案。因此，问题转化为在第二组数据中，求取最长的递增子序列即LIS的弱化版。

/*cen：原始数据
*low:当前起始位置
*ran:当前序号
*maxr:最长长度
*ree:中间结果
*res:set去重
*/
void getAllChildren(vector<pair<char, int>> cen, int low ,int ran, int maxr,string &ree,set<string>& res)
{
    string re = "";
    re = ree;
    for (int i = low; i < sz(cen)-1; i++) {
        if (cen[i].second == ran) {
            ree += cen[i].first;
            if (ran == maxr)    res.insert(ree);
            if (ran + 1 > maxr)        getAllChildren(cen, i + 1, ran + 1, maxr, ree, res);
            ree = re;
        }        
    }
    return;
}