字典算法经典生成算法
字典序的定义不再赘述。本篇暂不考虑递归实现。经典生成算法步骤如下。

函数结构如下。
1 //交换 a[u] 和 a[o] 2 template <typename T> 3 void swap(T *a,int u,int o); 4 5 //找到满足Pj-1 < Pj 的i 6 template <typename T> 7 int findMaxi(T *a,int length); 8 9 //找到满足Pi-1 < Pk 的J 10 template <typename T> 11 int findMaxJ(T *a,int length,int i); 12 13 //将下标start到end的数组反转 14 template <typename T> 15 bool reverseArr(T *a,int start,int nend); 16 17 //判断是否降序 18 template <typename T> 19 bool isAllDescend(T *a,int length); 20 21 //求解下一个 22 template <typename T> 23 void nextArr(T *a,int length);
整个流程如下:
1 do{ 2 for(int i=0;i<length;i++){ 3 cout<<ch[i]<<" "; 4 } 5 cout<<endl; 6 nextArr(ch,length); 7 }while(!isAllDescend(ch,length));
结果如下:
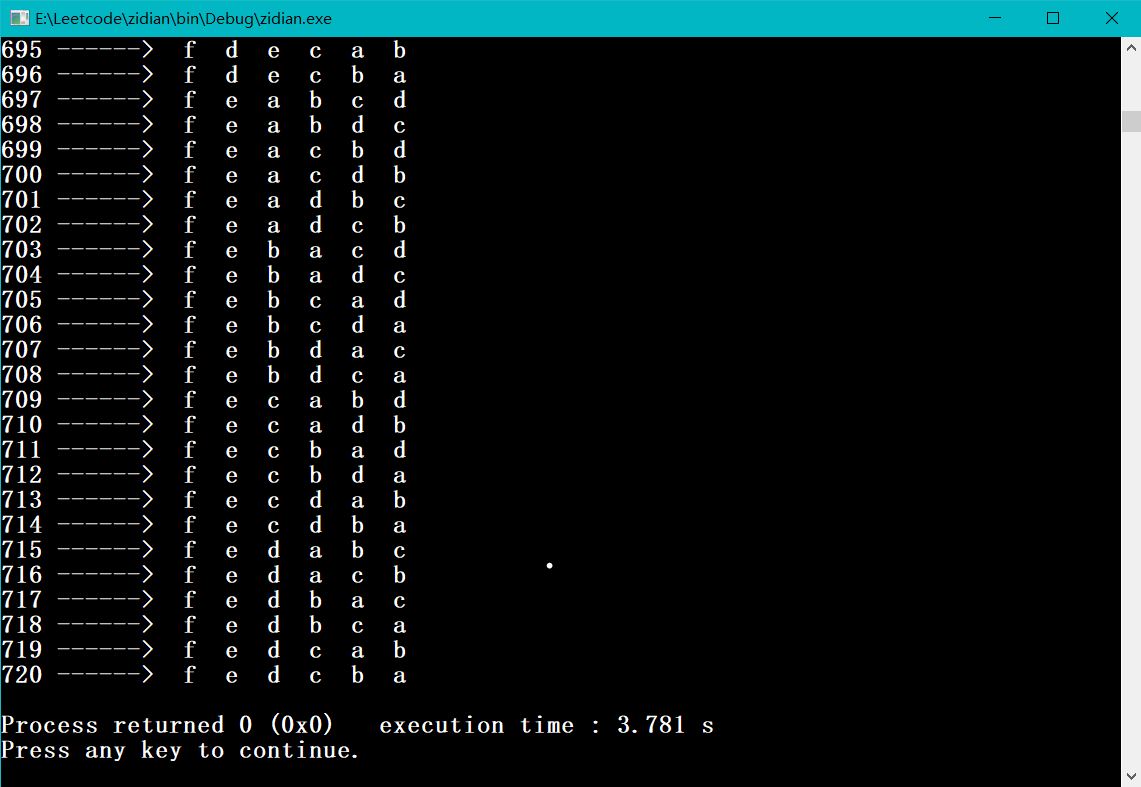
具体代码如下。下一篇写一下如何使用递归算法实现。
1 template <typename T> 2 void swap(T *a,int u,int o){ 3 T temp; 4 temp = a[u]; 5 a[u] = a[o]; 6 a[o] = temp; 7 } 8 9 template <typename T> 10 int findMaxi(T *a,int length){ 11 int mi = 0; 12 for(int i=0;i<length-1;i++){ 13 if(a[i]<a[i+1]) 14 if(i>mi) 15 mi = i; 16 } 17 18 return mi+1; 19 } 20 21 template <typename T> 22 int findMaxJ(T *a,int length,int i){ 23 int pi = a[i-1]; 24 int MJ = i-1; 25 26 for(int j=i;j<length;j++){ 27 if(a[j]>pi) 28 MJ = j; 29 } 30 31 return MJ; 32 } 33 template <typename T> 34 bool reverseArr(T *a,int start,int nend){ 35 for(int i=start;i<=(start+nend)/2;i++){ 36 swap(a,i,nend-i+start); 37 } 38 return true; 39 } 40 template <typename T> 41 bool isAllDescend(T *a,int length){ 42 43 for(int i=0;i<length-1;i++){ 44 if(a[i]<a[i+1]) 45 return false; 46 } 47 48 return true; 49 50 } 51 52 template <typename T> 53 void nextArr(T *a,int length){ 54 55 int i = findMaxi(a,length); 56 int j = findMaxJ(a,length,i); 57 58 swap(a,i-1,j); 59 60 reverseArr(a,i,length-1); 61 }


