C++ 神经网络初尝试

人言落日是天涯，望极天涯不见家。
已恨碧山相阻隔，碧山还被暮云遮。

　　　　　　　　　　　 　--李覯

 

用C++ eigen库对《 Neural networks and deep learning 》中python代码的复现。目前最好正确率仅在94%左右，迫于期末事儿多，暂时存档记录一下。来日方长，先放一放。

 

 

main()函数展示一下基本流程：

int main()
{

    int b[] = { 784,60,10};   //网络结构
    int len = sizeof(b) / 4;

    vector<batch> datas;
    vector<batch> testdatas;

    Network N(b,len);
    N.saveParameters("E:/shujuji/shouxie/y.txt");     //保存一下初始化参数

    cout << "请求读取数据集。。。。。。。。。。" << endl;

    string filename = "E:/shujuji/shouxie/train-images.idx3-ubyte";
    string filename1 = "E:/shujuji/shouxie/train-labels.idx1-ubyte";
    datas = loadData(filename,filename1,-1);   

    cout << "读取成功！！！" << endl;
    cout << "数据集大小：" << datas.size() << endl;
    cout << "数据格式： (" << datas[2].x.rows() << ", " << datas[2].x.cols() << " )" << endl;

    string filename2 = "E:/shujuji/shouxie/t10k-images.idx3-ubyte";
    string filename3 = "E:/shujuji/shouxie/t10k-labels.idx1-ubyte";
    testdatas = loadData(filename2, filename3,10000);

    cout << "读取成功！！！" << endl;
    cout << "数据集大小：" << testdatas.size() << endl;
    cout << "数据格式： (" << testdatas[2].x.rows() << ", " << testdatas[2].x.cols() << " )" << endl;

    N.SGD(datas,20,10,(double)3);   //SGD算法开始训练
    N.testDatas(testdatas);        //测试

    return 0;
}

 

 

对于每个照片数据和标签的定义如下：

struct batch {
    MatrixXd x;   //(784,1)的矩阵
    double y;　　　//标签
};

 

对与数据的读取上篇文章有所提及，经过实际的训练，有几点需要注意：数据集中的像素值是（0~255）的灰度值，需要对其进行归一化：

double dpix = pix/255.0;

或者反相：

double dpix = （255-pix）/255.0;

但实际测试中效果不太好，正确率只有70%左右。

考虑了二值化：

double dpix = (pp <= 125) ? 0 : 1;

效果提升较明显。

对于神经网络的初始化：

Network::Network(int size[], int num_lay) {

    for (int i = 0; i < num_lay; i++)
    {
        if (i > 0) {
            MatrixXd biase = Eigen::MatrixXd::Random(size[i], 1);
            Network::biases.push_back(biase);
        }
        if (i < num_lay - 1) {
            MatrixXd weight = Eigen::MatrixXd::Random(size[i+1], size[i]);
            Network::weights.push_back(weight);
        }
    }
}

 

随机梯度下降算法：思想就是通过随机选取⼩量训练输⼊样本来计算 ∇Cx，进⽽估算梯度 ∇C。通过计算少量样本的平均值我们可以快速得到⼀个对于实际梯度 ∇C 的很好的估算，这有助于加速梯度下降，进⽽加速学习过程。

 

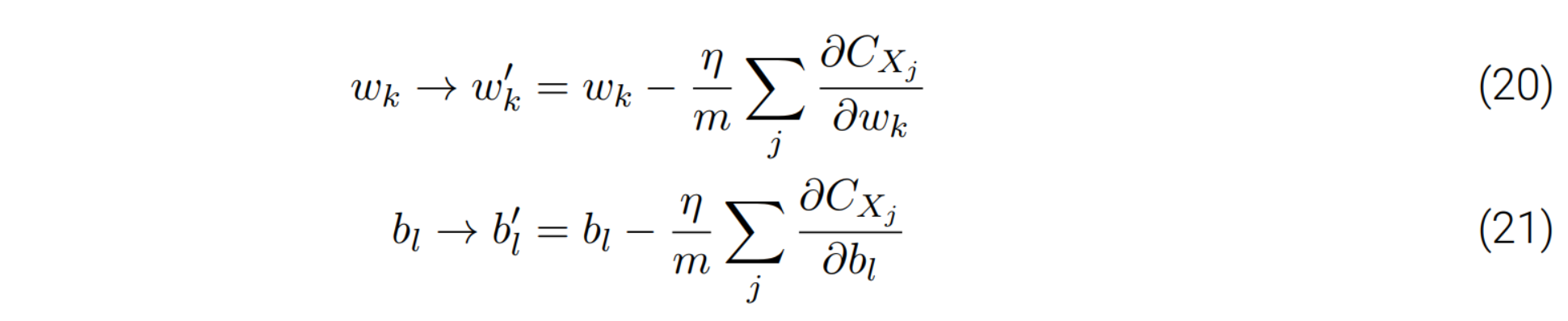
SGD( ):

void Network::SGD(vector<batch> traindata, int epochs, int mini_batch_size, double eta)  //epoxhs 训练轮次；mini_batch_size  随机选取⼩量训练输⼊样本的个数； eta 学习率；
{
    int len = traindata.size();

    for (int e = 1; e <= epochs; e++)
    {
        cout << "。。。。。。。。。。。。。。。。。。"<<endl;
        cout << "开始第" << e << "轮训练。。。" << endl;
        randomshuffle(traindata);
        //batch *bs = new batch[mini_batch_size] ;
        vector<batch> bs;

        for (int i = 0; i < len; i += mini_batch_size) {
            bs.clear();
            for (int j = i; j < i+mini_batch_size; j++) {
                if (j > len) break;
                bs.push_back(traindata[j]);
            }
            update_mini_batch(bs,eta,mini_batch_size);
        }
    }

    string Pfilename = "E:/shujuji/shouxie/p.txt";

    if (Network::saveParameters(Pfilename)) {
        cout << "训练完成。。。" << endl;
        cout << "参数成功输出。。。" << endl;
    }
}

 

 

void Network::update_mini_batch(vector<batch> minibatch, double eta,int mlength)
{
    vector<MatrixXd> nabla_b;
    vector<MatrixXd> nabla_w;
    vector<MatrixXd> delta_nabla_b;
    vector<MatrixXd> delta_nabla_w;

    for (int i = 0; i < Network::biases.size(); i++)
    {
        MatrixXd bia(Network::biases[i].rows(), Network::biases[i].cols());
        bia.setZero();
        MatrixXd dbia(Network::biases[i].rows(), Network::biases[i].cols());
        dbia.setZero();
        nabla_b.push_back(bia);
        delta_nabla_b.push_back(dbia);
    }

    for (int n = 0; n < Network::weights.size(); n++)
    {
        MatrixXd wei(Network::weights[n].rows(), Network::weights[n].cols());
        wei.setZero();
        MatrixXd dwei(Network::weights[n].rows(), Network::weights[n].cols());
        dwei.setZero();

        nabla_w.push_back(wei);
        delta_nabla_w.push_back(dwei);
    }


    for (int i = 0; i < mlength; i++) {

        MatrixXd x = minibatch[i].x;
        double y = minibatch[i].y;

        Network::backprop(x, y, delta_nabla_b, delta_nabla_w);

        for (int n = 0; n < delta_nabla_b.size(); n++) {
            nabla_b[n] = nabla_b[n] + delta_nabla_b[n];
        }

        for (int j = 0; j < delta_nabla_w.size(); j++) {
            nabla_w[j] = nabla_w[j] + delta_nabla_w[j];
        }

    }

    int len = minibatch.size();

    for (int i = 0; i < Network::biases.size(); i++)
    {
        Network::biases[i] = Network::biases[i] - (eta / len)*nabla_b[i];
    }

    for (int i = 0; i < Network::weights.size(); i++)
    {
        Network::weights[i] = Network::weights[i] - (eta / len)*nabla_w[i];
    }

}

 

 

 

 

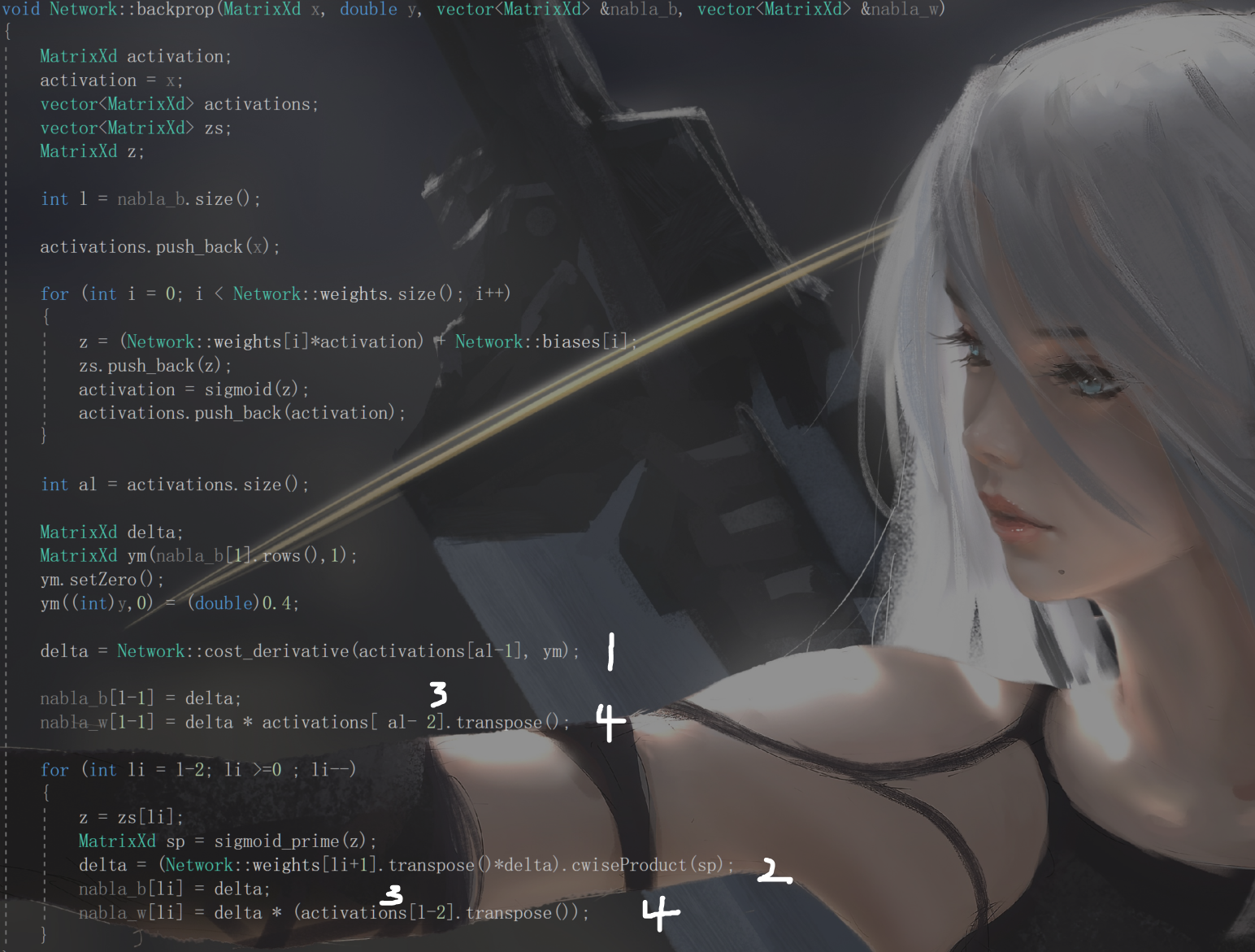
对标签数据集y定义为（ 0, 0, 0, 0，1, 0, 0, 0, 0, 0 ），但测试中值在0.4左右效果最好；

 

依据如下公式：

 

 

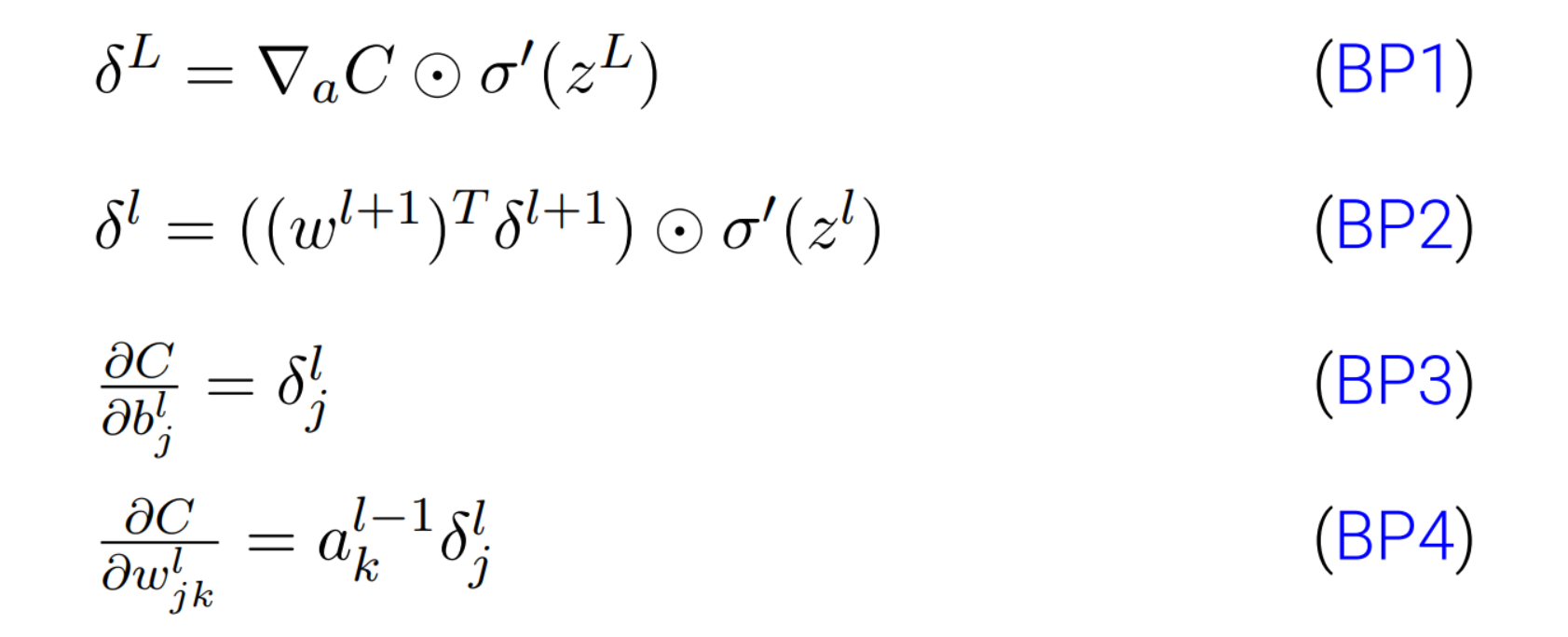
***对于语句1，因为用的交叉熵作为损失函数，激活函数的导数被约去。

 

补充一点eigen中exp() 函数的用法：

 

MatrixXd sigmoid(MatrixXd z) {
    MatrixXd zt;
    zt = (-z).array().exp().matrix();
    MatrixXd o(z.rows(), z.cols());
    o.setOnes();
    return  (o+zt).cwiseInverse();
}

MatrixXd sigmoid_prime(MatrixXd z) {

    MatrixXd o(z.rows(), z.cols());
    o.setOnes();
    return sigmoid(z).cwiseProduct(o - sigmoid(z));
}

 

eigen中矩阵（MatrixXd）乘法直接使用“ * ”即可，对应项相乘使用 cwiseProduct(  )；

类似的 cwiseInverse() 每个元素取倒数。