理解卷积
文章抄自知乎 刘洪
在计算机视觉领域,卷积(Convolution)的地位就如同水泥之于建筑行业,理解卷积是理解CV领域中深度学习的基础。
前言
计算机处理的图像都是离散的数字表示,所以这里提到的卷积是指离散卷积。同时必须指出,这里的卷积不是数学上的卷积,而是数学上的cross-correlation。为便于理解卷积二字的含义,先从数学上的一维离散卷积开始。

如上面例子所示,“卷”字体现在将其中一个序列进行翻转,然后与另一个序列的元素对齐,脑补一下卷铺盖的场景。“积”字体现在两个序列的对应位置元素求乘积,最后再加在一起。
数学上cross-correlation是这样的:
深度学习里的卷积则是建立在cross-correlation基础上,计算公式如下:
其中N 表示 batch size,C 表示 channel,L 表示 length,padding 表示扩展的长度,kernel 表示卷积核(信号处理则叫filter),stride 表示两个序列对齐时,每次跳过的长度。举例说明如下:

如此鸠占鹊巢,只怪卷积(Convolution)朗朗上口,太好记。名字取得好,就是成功的一半。比如人工神经网络(ANN)发展到深度神经网络(DNN),本质上只是网络的层次加深了,再到深度学习(Deep Learning),同样的东西,造成的效果就是天壤之别了。高大上的名字,最能忽悠不懂的人。
卷积汇总
在计算机视觉领域,图像是用二维的矩阵表示的,因此接下来将聚焦到二维卷积(2-D Convolution)以及其主要变种上。
- Vanilla Convolution
基本的二维卷积公式与示例如下。 其中N 表示 batch size,C 表示 channel,H表示height,W表示witch,K表示kernel,P表示padding,S表示stride。输入输出也叫feature map。
由简入繁的动态示例如下,请用心体会卷积核的滑动这个动作。
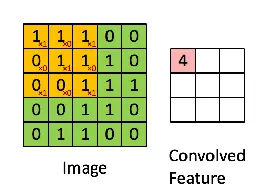
N=1,C_in=1,C_out=1,K_h=K_w=3,S_h=S_w=1,P_h=P_w=0
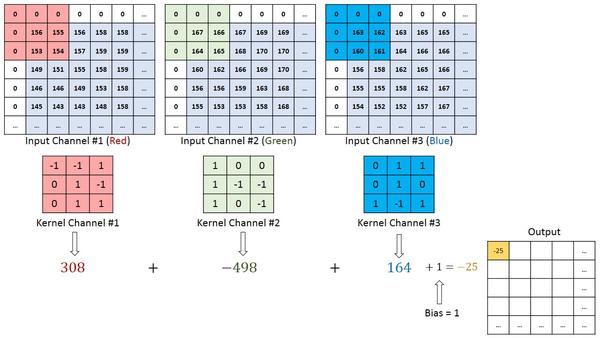
N=1,C_in=3,C_out=1,K_h=K_w=3,S_h=S_w=1,P_h=P_w=1
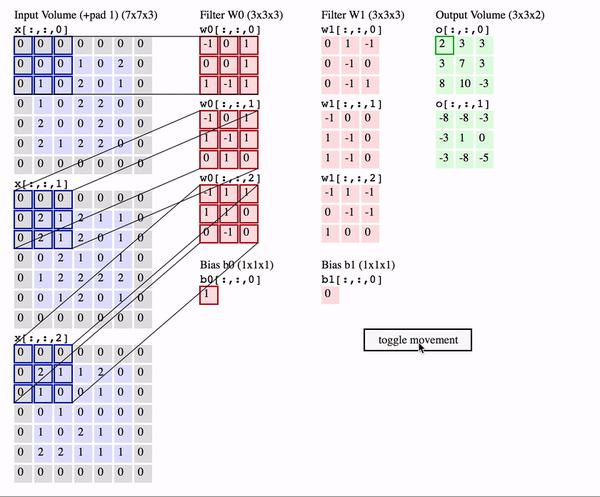
N=1,C_in=3,C_out=2,K_h=K_w=3,S_h=S_w=2,P_h=P_w=2,
在实际计算中,有不同的实现方式,比如GEMM(General matrix multiply),FFT(Fast Fourier Transform),Winograd[1]加速小卷积核的计算,caffe利用空间换时间的方法[2]等,这里有一个小问题供大家思考:如果一个卷积的输入形状为 [n, ic, ih, iw],卷积核形状为 [kh, kw],输出形状为 [n, oc, oh, ow],那么按照上面的公式计算卷积,要进行多少次乘法运算?这里没有告诉padding,stride,所以无法从输入到输出这个正向来分析。但是已知了输出形状,输出的每一个元素都是卷积核与输入中卷积核相同形状的矩阵与卷积核对应元素相乘,再求和,对每一个输入通道(channel),每一个输出元素需要 次乘法,每一个输出通道有
个元素,因此得到
。同时考虑到是输出的每一个元素,是所有输入通道对应矩阵与卷积核运算完之后的累加,因此乘法次数要再乘以
ic,得到。最后考虑输出通道与batch size,得到最终结果
。这个小问题想明白了,基本卷积运算就清楚了。
卷积的反向求导[3]
- Grouped Convolution
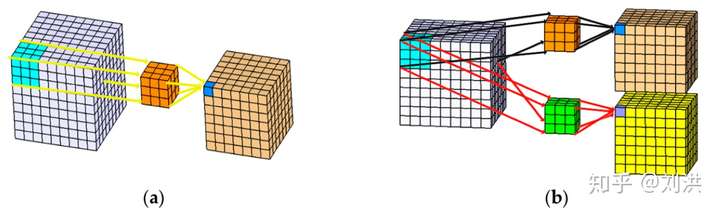
这种卷积是在2012年ImageNet上横空出世的AlexNet[4]中首次提出的,大神Alex(导师是Hinton)为了充分利用两块Nvidia GTX 580 GPU(每块1.5GB显存)而设计出来的。核心思想是将input 与 kernel 都进行分组,这样每块GPU就可以独立并行计算了,分别计算出的结果再拼凑成output,如下图所示[5]。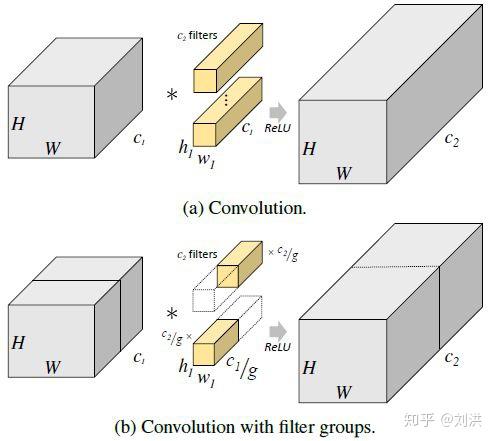
如果原始的卷积核shape是 ,现在要分成
个组,则分组后的卷积核为
。参数量为原来的
, 计算量也为原来的
。可以看出减少了参数量与计算量,然而不同分组之间却没有做信息交互。随着之后GPU性能越来越强,后来的网络中很少再出现这种卷积了。
- Depthwise Separable Convolution
为了利用分组卷积参数少计算快的优点,同时克服缺乏信息交互的缺点,深度可分离卷积应运而生。首先将分组分到极致,每一个input channel分成一个组,output channel与input channel相同,此时kernel shape 为 [ic,1,kh,kw], 叫 Depthwise Convolution;再将上一步的所有output channel融合,kernel shape 为 [oc,ic,1,1],output channel 为 oc,叫 Pointwise Convolution。总参数量为 。在Xception[6]和MobileNet[7]中有均有应用。
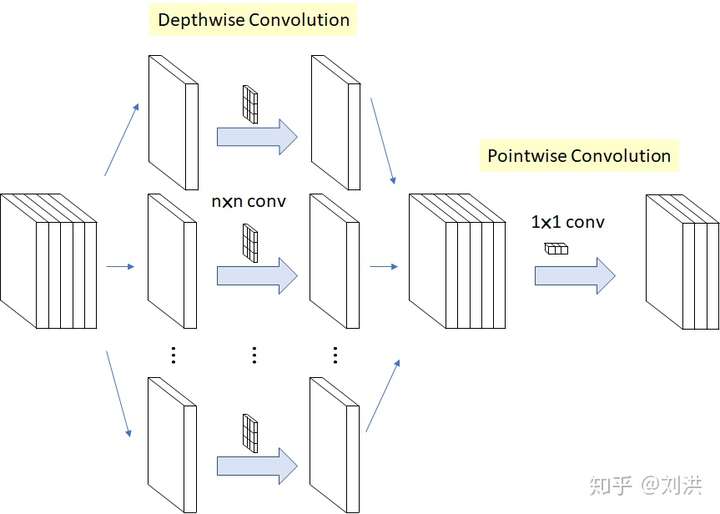
- Transposed Convolution
我们知道乘法的逆运算是除法,那么卷积的逆运算是什么呢?通常将一个大的featrue map通过卷积得到一个小的featrue map以得到深层特征,反之如何用这个小的featrue map得到原来大的featrue map 呢?Deconvolution 或者叫 Transposed Convolution 出场了,然而只是形似,不是真正的逆运算,个人觉得叫Deconvolution并不合适,只是名字简短好记。假设有卷积 ,
表示输入,
表示卷积核,
表示输出;与之对应的 Transposed Convolution 为
, 则有
,只是二者形状相同而已。也许正是因为不是真正的逆运算,才取名为 Transposed Convolution,而且“Transposed”也不应该理解为转置,而是“a transformation as the decoding layer of a convolutional autoencoder”。实际上,在对
做Transposed Convolution时,kernel 与
到
做卷积时是不一样的(只是形状一样),padding也不一样(因为需要增加一项output padding),stride 则不一定一样[8]。 除以上区别外,Transposed Convolution 的计算是和Convolution一样的,也就是是说依然使用Convolution的形式去计算Transposed Convolution 。下面一系列动图将展示二者的区别。
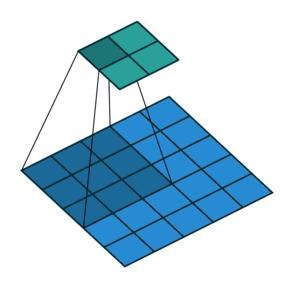
Convolution-no padding, no stride
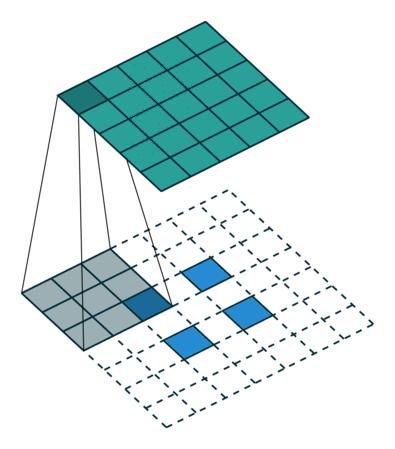
Transposed Convolution-no padding, no stride
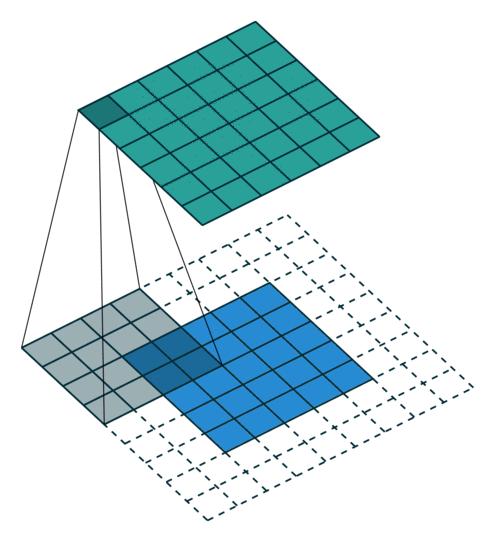
Convolution-arbitrary padding, no stride
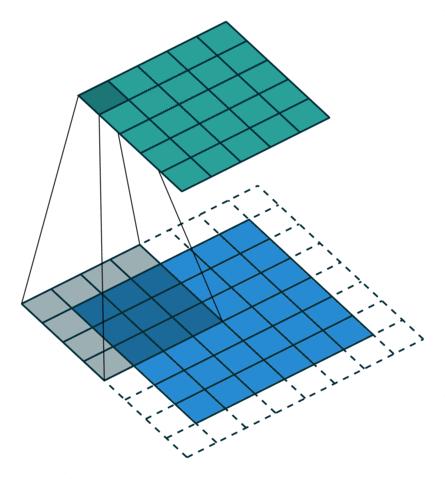
Transposed Convolution-arbitrary padding, no stride

Convolution-no padding, with stride

Transposed Convolution-no padding, with stride
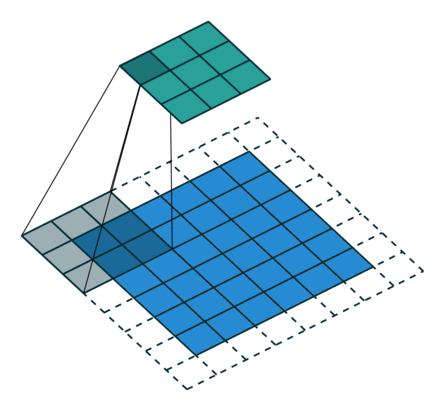
Convolution-with padding and stride
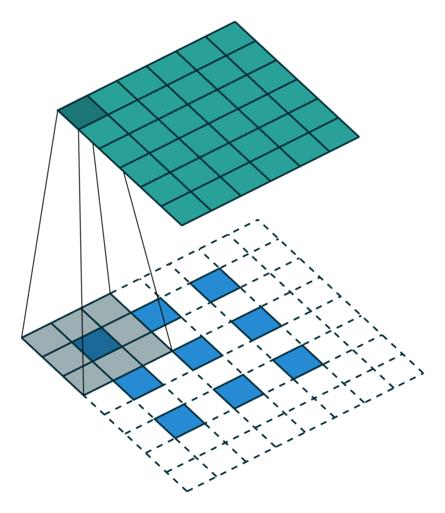
Transposed Convolution-with padding and stride
从上面最后一图看出,做Transposed Convolution 时对输入做了插0操作(内部虚线方格),这样对于原始输入,每一次stride跳过的就不是一个或多个元素的位置了,有时可以认为小于1。基于这个思路, Transposed Convolution也叫lFractionally-strided Convolution。到底中间应该插入多少行/列的0呢?规定为原来卷积的stride - 1。当插入0之后,计算卷积时,真正的stride 就变成了1。细心的读者还发现上图右侧比左侧多了一列虚线方格,这是怎么回事呢?其实我们现在还没有确定Transposed Convolution的padding,这是可以计算出来的。

假设Transposed Convolution 的输入的height 为 ,输出height 为
。鉴于Convolution 与 Transposed Convolution 的关系,利用卷积计算输出形状的公式有
,反过来用
表示
,为了取消向下取整函数的影响,添加了一项
,得到上图(1)式。真正计算Transposed Convolution时,通过插0后,得到
,即上图(2)式;进而模拟卷积进行计算,因此有上图(3)式。最后推导出output padding的值,如上图(6)式。
- Dilated Convolution
在介绍Dilated Convolution之前,先补一下感受野[9](receptive field)的知识。The receptive field is defined as the region in the input space that a particular CNN’s feature is looking at (i.e. be affected by)。在CNN中,当卷积层数不断叠加时,后面卷积层输出的feature map中每个特征会受到前面层的feature map中多大区域的影响?这个区域就是感受野,其大小是可以计算的,如下图。计算细节这里不再赘述,请查阅引用链接。
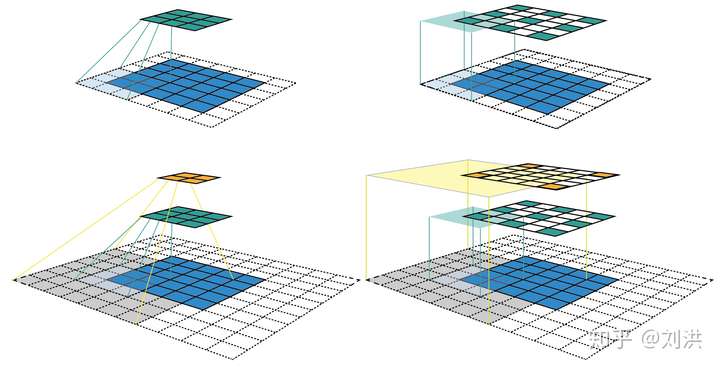
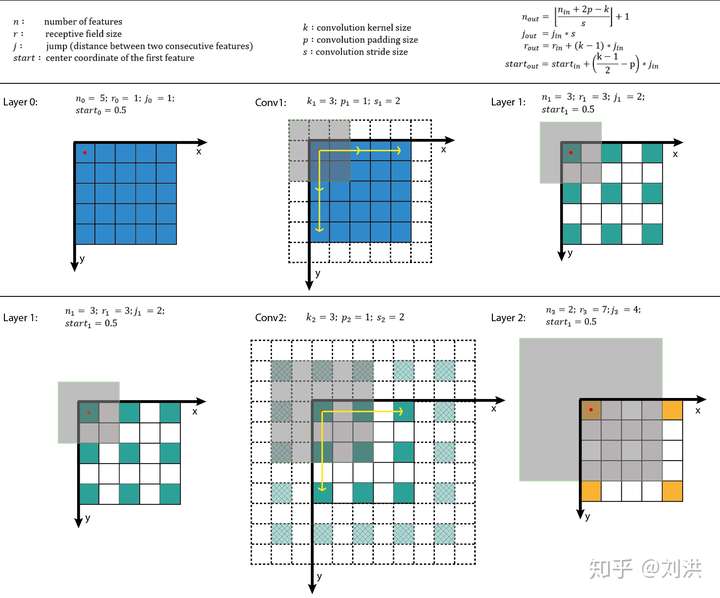
通过计算感受野大小,可以帮助卷积层的设计。比如连续两个的 卷积与一个
卷积输出的感受野是一样的,那么完全可以用两个
卷积替代,因为参数少,而且可以用Winograd加速,这也是AlexNet之后很少出现像
的大卷核的原因。另一方面,不是卷积层数叠加越多越好,到某一层时,其输出特征的感受野已经覆盖了网络输入的全部特征,就没有必要继续叠加卷积了。
为了增大感受野范围,除了上述采用大卷积核、堆叠多个小卷积核外,Dilated Convolution 登场了。Dilated convolutions are used to cheaply increase the receptive field of output units without increasing the kernel size. Dilated convolutions support exponential expansion of the receptive field without loss of resolution or coverage[10]. Dilated Convolution [11]还有别名,Atrous Convolution,与 Convolution with holes。之前的Transposed Convolution是在输入的feature 中插入0来进行扩展,而Dilated Convolution 则是通过在卷积核内部插入0的方式来扩展卷积核,进而在不增加参数的情况下,扩大感受野范围,如下图所示,下方feature map 中深色方格表示卷积核。
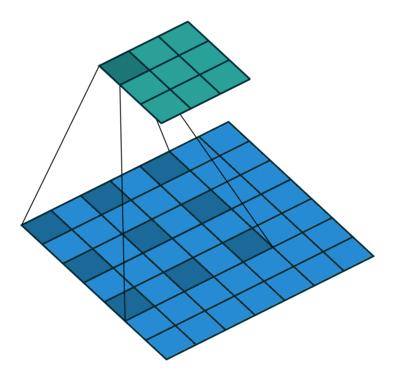

对于一个kernel size 为 的卷积核,设置dilation rate为
,则有效卷积核大小为
假设输入的height、width相同且都为 ,kernel size 为
,padding 为
,stride 为
,dilation rate 为
,则输出height、width相同,记为
,则有
- Octave Convolution[12]
我们知道信号中有高频信号,低频信号,使用小波分解等方法,可以将高低频信号分离出来,进而做不同处理,比如将某些高频噪声去除掉。同样的,图像中也有高频与低频,如下图所示。左上图是原始图像,上中图是低频特征,上右图是高频特征。而之前的卷积都是一视同仁,并不做区分。
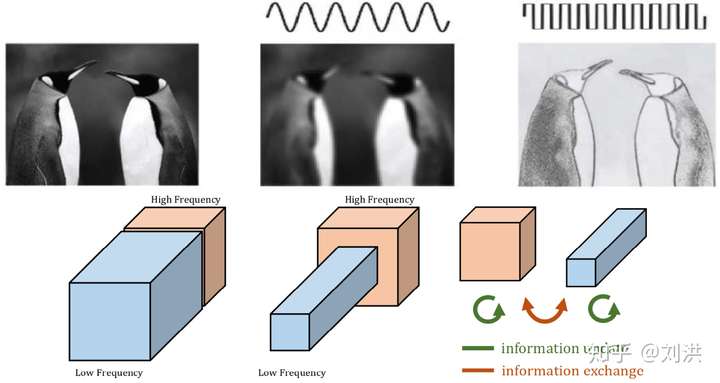
如何将高频特征与低频特征分离呢?分离之后需不需要再交互信息?怎样交互?如下图,kernel 也要重新设计,划分为 ,
,
,
。论文中取的
,是不是有种Attention的感觉?
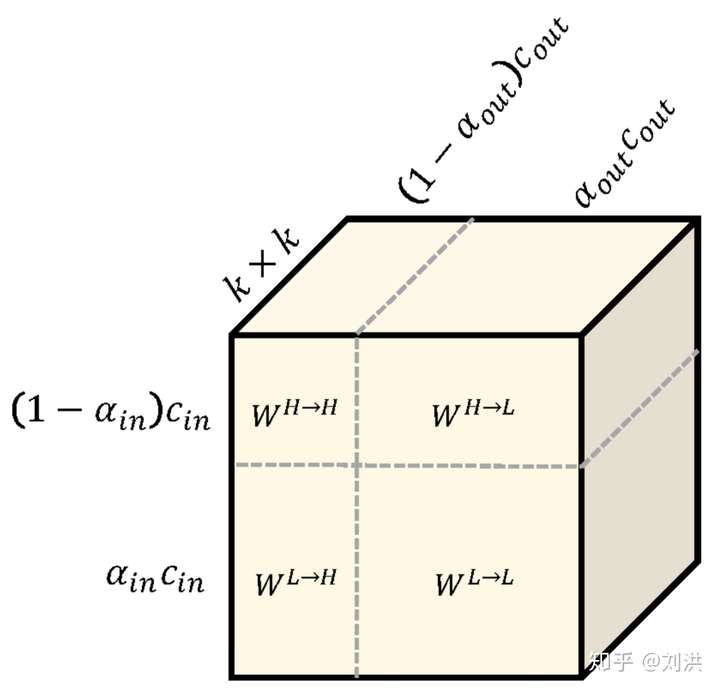
接下来看详细的计算过程,如下图,这里公式推导不再赘述,请查看论文或其他文章[13]。
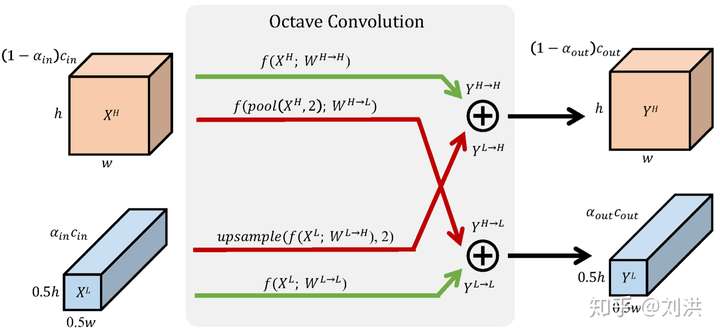
好处也是大大的,即插即用,分类网络中替换掉传统卷积之后,在ImageNet上的识别精度能获得1.2%的提升,同时,只需要82%的算力和91%的存储空间,而且网络结构都不用修改。
- 3-D Convolution
三维卷积比二维卷积多了一个维度:Depth,计算上差不多,此时的输入叫Voxedlized Point Cloud,目前没有二维卷积应用广泛。
后记
阅读了以上内容后,对卷积应该有了深入的理解。最后再单独抛出一个问题:卷积核的大小为何是总是选择奇数而不是偶数?[14]
其实,奇数可以写成 ,是有中心点的。回想卷积计算时卷积核的滑动,我们完全可以只关注卷积核中心点的滑动;对应的,我们也可以很容易找到输出结果中每一个特征中对应的收入特征区域的中心位置。其次,如果是偶数,则有可能在padding时左右或上下padding的值不一样,提取的特征会发生偏移。有人用偶数大小的卷积核做过实验,发现模型效果下降很多。


