Gym 100827G Number Game （博弈）

Number Game

Alice and Bob are playing a game on a line of N squares. The line is initially populated with one of each of the numbers from 1 to N. Alice and Bob take turns removing a single number from the line, subject to the restriction that a number may only be removed if it is not bordered by a higher number on either side. When the number is removed, the square that contained it is now empty. The winner is the player who removes the 1 from the line. Given an initial configuration, who will win, assuming Alice goes first and both of them play optimally?

Input
Input begins with a line with a single integer T, 1 ≤ T ≤ 100, denoting the number of test cases. Each test case begins with a line with a single integer N, 1 ≤ N ≤ 100, denoting the size of the line. Next is a line with the numbers from 1 to N, space separated, giving the numbers in line
order from left to right.

Output
For each test case, print the name of the winning player on a single line.

Sample Input

4 4
2 1 3 4
4
1 3 2 4
3
1 3 2
6
2 5 1 6 4 3

Sample Output

Bob
Alice
Bob
Alice

题意：输入一个N, 然后给一个1~N的数列。两个人轮流拿数字，当一个数字两边没有比它大的数字的时候（旁边是空格也可以），这个数字就可以被拿走。

题解：

考虑到如果要拿1，就要先把1旁边的两个数都拿走，那么如果1旁边两个数其中的一个已经被拿走，两个人肯定是不想拿剩下的一个数，所以此时所走的步数已经确定。Alice作为先手，优势就是选择两数之一。1在旁边特殊考虑一下，其实原理是一样的。

画个图表示下（略抽象）：

 

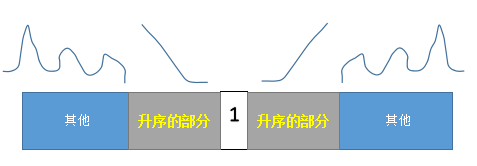
附上几组数据：

8
7 3 5 2 4 1 6 8
6
1 5 3 4 2 6
7
7 2 4 6 3 1 5
6
1 5 3 4 2 6
5
3 4 1 5 2

Bob
Alice
Alice
Alice
Bob

代码：

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N = 100005;
int a[N];

// 窝乃辣鸡
// 感谢小杭=.=

bool MDZZ()
{
    int n;
    scanf("%d", &n);
    int pone, pl, pr;
    pl = 0; pr = n+1;
    for (int i = 1; i <= n; ++i) {
        scanf("%d", a+i);
        if (a[i] == 1) pone = i;
    }
    for (int i = pone - 1; i > 1; --i) {
        if (a[i] < a[i-1]) { pl = i-1; break; }
    }
    for (int i = pone + 1; i < n; ++i) {
        if (a[i] < a[i+1]) { pr = i+1; break; }
    }
    int ex = (n - pr + 1) + (pl);

    int ls = pone - pl - 1; // 左边中间的
    int rs = pr - pone - 1; // 右边中间的

    if (n == 1) return true;

    // 如果1在最左边或者最右边
    if (pone == 1 || pone == n) {
        if ((ex+1) % 2 == 0) return true;
    }
    // 1不在边上
    else{
        bool f = false;
        // 能先拿1左边的数
        if ((pl == 0) || (ls > 1)) {
            if ((ex+ls+1) % 2 == 0) return true;
            f = true;
        }
        // 能先拿1右边的数
        if ((pr == n+1) || (rs > 1)) {
            if ((ex+rs+1) % 2 == 0) return true;
            f = true;
        }
        // 1左右的数都不能拿 必须把全部的拿走才行
        if (!f && n % 2 == 1) return true;
    }
    return false;
}

int main()
{
    int t;
    scanf("%d", &t);
    while (t--) puts(MDZZ() ? "Alice" : "Bob");
    return 0;
}