HDU 3392 Pie(DP)

题意：有一些男生女生，男生女生数量差不超过100 ，男生女生两两配对。要求求出一种配对方法，使每一对的高度差的和最小。

思路：（我是真的笨笨笨！！）设人少的一组人数为n,b[]，人多的一组人数为m,g[](b[],g[]先排好序)，用dp[i][j]表示n中的前i个人与m中的前j个人配对所得到的最小值。

对于每个i，j的范围是（i~i+m-n）

 

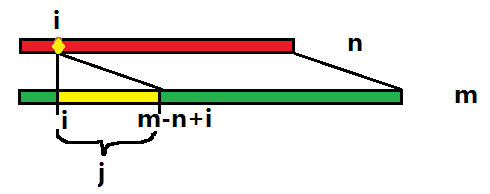
这样j的范围是i~m-n+i，对于dp数组而言，第二维数组要开到m，由于数组过大，而我们又知道，m-n<=100，所以用j表示j-i，j的范围就变成了(0~m-n)，也就是(0~100)，这种情况下dp[i][j]表示b中前i个人和g中前i+j个人的最小值。

对于每一个dp[i][j]它的可能就是选第i+j个，不选第i+j个数。

如果不选的话，那么dp[i][j]就等于dp[i][j-1]，如果选了呢，就是dp[i-1][j]+|b[i]-g[i+j]|

状态转移方程：dp[i][j]=min(dp[i][j-1], dp[i-1][j] + |b[i]-g[i+j]|)

AC代码：

/** hdu 3392 */

#include <iostream>
#include <algorithm>
#include <cstring>
#include <cmath>
using namespace std;

const int N = 10005;
double a[N], b[N];
double dp[N][110];

double getdp(int m, int n, double *g, double *b)
//m，g为人数多的一组，n,b为人少的一组
{
    for (int i = 1; i <= n; ++i) {
        dp[i][0] = dp[i - 1][0] + fabs(b[i] - g[i]);//对于dp[...][0],即两组个数相等，没有选择~
        for (int j = 1; j <= m - n; ++j) {
            dp[i][j] = min(dp[i - 1][j] + fabs(b[i] - g[i + j]), dp[i][j - 1]);
        }
    }
    return dp[n][m - n];
}

int main()
{
    //freopen("in.txt", "r", stdin);
    int  boys, girls;
    while (scanf("%d%d", &boys, &girls) != EOF && (boys || girls)) {
        for (int i = 1; i <= boys; i++) {
            scanf("%lf", &a[i]);
        }
        for (int i = 1; i <= girls; i++) {
            scanf("%lf", &b[i]);
        }
        sort(a + 1, a + 1 + boys);
        sort(b + 1, b + 1 + girls);
        double ans;
        if (boys < girls)
            ans = getdp(girls, boys, b, a);
        else
            ans = getdp(boys, girls, a, b);
        printf("%f\n", ans);
    }
    return 0;
}

但是看了别人的博客，可以用到滚动数组【啊喂！！我就是为了学一下滚动数组才搜到这道题的，结果根本不用啊！】。

滚动数组很神奇啊，因为对于每一个dp[i]，求它的过程只与dp[i-1]有关，所以开成2个就够了。既dp[2][...]

代码

/** hdu 3392 */

const int N = 10005;
double a[N], b[N];
double dp[2][110];

double getdp(int m, int n, double *g, double *b)
//m，g为人数多的一组，n,b为人少的一组
{
    memset(dp, 0, sizeof(dp));
    for (int i = 1; i <= n; ++i) {
        dp[i % 2][0] = dp[(i - 1) % 2][0] + fabs(b[i] - g[i]);
        for (int j = 1; j <= m - n; ++j) {
            dp[i % 2][j] = min(dp[(i - 1) % 2][j] + fabs(b[i] - g[i + j]), dp[i % 2][j - 1]);
        }
    }
    return dp[n % 2][m - n];
}

改了之后注意加一句memset(dp, 0, sizeof(dp));

因为窝之前的dp[0][..]是没有用到的，一直是0……所以不用

对于这种通过%N...来节省数组空间的方法窝觉得真是太神奇了orz……

继续努力~