HDU1710Binary Tree Traversals
题目大意:给一个树的前序遍历和中序遍历,要求输出后序遍历。
(半年前做这道题做了两天没看懂,今天学了二叉树,回来AC了^ ^)
首先介绍一下二叉树。二叉,即每个节点最多连向下连两个结点,也就是最多两个孩子。
如题目描述,二叉树就长这样~
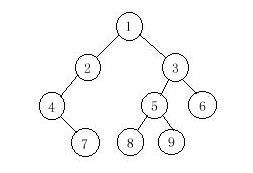
如①②③结点中①是根节点,②是左儿子③是右儿子,其余类似。
前序遍历就是先根节点,然后左儿子,右儿子
中序遍历就是先左儿子,然后根节点,右儿子
后序遍历就是先左儿子,然后右儿子,最后根节点
也就是说前中后描述的是访问根节点的顺序~
通过递归可以很简单遍历二叉树。
首先定义结构体BiTree为二叉树结点
struct BiTree
{
int data;
BiTree * l, *r;//左右儿子
};
前序
void print_qx(BiTree *t)
{
if (t != NULL)
{
printf("%d ", t->data);
print_qx(t->l);
print_qx(t->r);
}
}
中序
void print_zx(BiTree *t)
{
if (t != NULL)
{
print_zx(t->l);
printf("%d ", t->data);
print_zx(t->r);
}
}
建树麻烦一些,不过也可以通过递归实现。首先,我们知道
这样我们就能找到根节点,然后把左子树和右子树通过递归再去建树。最后一层要返回BULL,表示结束。
AC代码如下:
#include <iostream>
#include <cstring>
#include <cstdlib>
#include <cstdio>
using namespace std;
struct BiTree
{
int data;
BiTree * l, *r;
} *tr;
int qx[1005];
int zx[1005];
BiTree* build(int *a, int *b, int n)
{
BiTree * t = (BiTree *)malloc(sizeof(BiTree));
//根据前序和后序构造树
for (int i = 0; i < n; i++)
{
if (a[0] == b[i])
{
t->data = a[0];
t->l = build(a + 1, b, i);
t->r = build(a + i + 1, b + i + 1, n - i - 1);
return t;
}
}
return NULL;
}
void print_hx(BiTree *t)
{
if (t != NULL)
{
print_hx(t->l);
print_hx(t->r);
if (t == tr)//根据后序遍历规律,如果是根节点,则是最后一个数字……
printf("%d\n", t->data);
else
printf("%d ", t->data);
}
}
int main()
{
int n;
while (cin >> n)
{
for (int i = 0; i < n; i++)
cin >> qx[i];
for (int i = 0; i < n; i++)
cin >> zx[i];
tr = build(qx, zx, n);
print_hx(tr);
}
return 0;
}
-----------更新分割线----------
经过我的深思熟虑(好吧是看了别人的题解),这道题可以直接输出后序遍历而不用再去建树,这样既节省时间又节省空间。
基本思想就是先处理左儿子再处理右儿子最后处理根节点(就是输出啦)。代码也少了不少~
具体做法如下
#include <cstring>
#include <cstdlib>
#include <cstdio>
int qx[1005];
int zx[1005];
void build(int *a, int *b, int n) {
// 根据前序和后序构造树
for (int i = 0; i < n; i++) {
if (a[0] == b[i]) {
build(a + 1, b, i);
build(a + i + 1, b + i + 1, n - i - 1);
if (a == qx)
printf("%d\n", a[0]);
else
printf("%d ", a[0]);
return;
}
}
}
int main() {
int n;
while (scanf("%d", &n) == 1) {
for (int i = 0; i < n; i++)
scanf("%d", qx + i);
for (int i = 0; i < n; i++)
scanf("%d", zx + i);
build(qx, zx, n);
}
return 0;
}
