课程作业02-汇总整理
1.使用组合数公式利用n!计算
设计思想:
利用组合数公式计算,通过对n、k、(n-k)的阶乘进行递归,实现求组合数。
程序流程图:
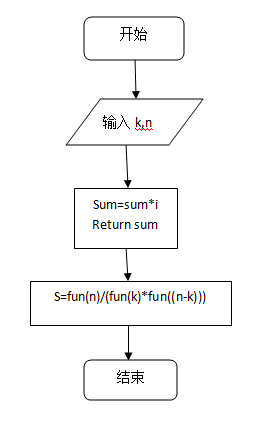
源程序代码:
package zuheshu;
import java.util.Scanner;
public class Zuheshu
{
public static void main(String[] args) {
long k,n,s;
Scanner input=new Scanner(System.in);
System.out.println("请输入k和n的值:");
k=input.nextInt();
n=input.nextInt();
s=fun(n)/(fun(k)*fun((n-k)));
System.out.print("计算结果为:"+s);
}
public static long fun(long n)
{
int sum=1;
for(int i=1;i<=n;i++)
{
sum=sum*i;
}
return sum;
}
}
结果截图:

2.使用递推的方法用杨辉三角形计算
设计思想:
杨辉三角可以反映组合数的值,通过递归建立杨辉三角,再通过杨辉三角输出组合数的值。
程序流程图:
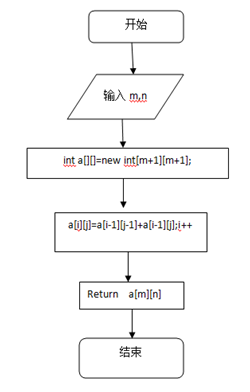
源程序代码:
import java.util.Scanner;
public class Zuheshu2
{
public static void main(String[] args)
{
Scanner input=new Scanner(System.in);
System.out.println("请输入n和m的值");
int n=input.nextInt();
int m=input.nextInt();
if(m<n)
{
System.out.println("输入错误!");
}
else
System.out.println("C"+"["+n+","+m+"]"+"="+yanghui(n,m));
}
public static int yanghui(int n,int m)
{
int a[][]=new int[m+1][m+1];
for(int i=0;i<m+1;i++)
{
for(int j=i+1;j<m+1;j++)
{
a[i][j]=0;
}
for(int j=0;j<=i;j++)
{
if(j==0)
{
a[i][j]=1;
}
else
{
a[i][j]=a[i-1][j-1]+a[i-1][j];
}
}
}
return a[m][n];
}
}
结果截图:

3.使用递归的方法用组合数递推公式计算
设计思想:
通过对组合数递推公式的递归实现,输出组合数的数值。
程序流程图:

源程序代码:
import java.util.Scanner;
public class Zuheshu3
{
public static void main(String[] args)
{
Scanner input=new Scanner(System.in);
System.out.println("请输入n和m的值");
int n=input.nextInt();
int m=input.nextInt();
System.out.println("C"+"["+m+","+n+"]"+"="+digui(n,m));
}
public static int digui(int n,int m)
{
if(m<n)
{
System.out.println("输入错误!");
}
if(n==1)
{
return m;
}
if(m==n)
{
return 1;
}
return digui(n-1,m-1)+digui(n,m-1);
}
}
结果截图:

4.汉诺塔问题
设计思想:
1.首先利用界面将输出语句输出;
2.设置abc三个字符型变量用来表示三个塔;
3.定义一个move函数,用来存储汉诺塔解决的方法;
4.当m(环的个数)=1时,直接将盘子从a移动到c即可;
5.如果盘子个数超过2,就用递归的思想解决;
6.第一处递归:move(m-1,a,c,b)实现将m-1个环从a,借助c,移动到b
7.a->c实现将第n个环从a移动到c
8.第二处递归:move(m-1,b,a,c)实现将m-1个环从b,借助a,移动到c
程序流程图:
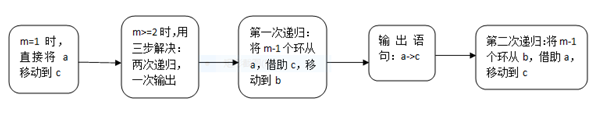
源程序代码:
//汉诺塔问题
package hannuota;
import javax.swing.JOptionPane;
public class main {
public static void main(String args[])
{
String s=" ";
s=JOptionPane.showInputDialog("请输入环的个数");
int j=0;
char a='a',b='b',c='c';
j=Integer.parseInt(s);
move(j,a,b,c);
}
public static void move(int m,char a,char b,char c)
{
if(m==1)
{
System.out.println(a+"->"+c);
}
else
{
move(m-1,a,c,b);
System.out.println(a+"->"+c);
move(m-1,b,a,c);
}
}
}
结果截图:
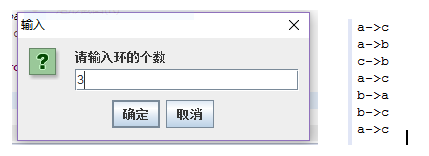

5.回文字符串问题
设计思想:
1.首先定义main函数,定义两个整型变量i,j用来表示字符串的位置下标,从零开始。
2.接着定义一个布尔类型的函数judge用来判断字符串是否为回文字符串。
3.如果字符串长度为1,直接返回true
4.如果字符串长度大于1,则递归判断。每次判断结束后,i+1,j-1,直到判断结束。
程序流程图:

源程序代码:
//输入一个字符串,判断其是否为回文字串
package palindrome;
import java.util.Scanner;
public class Huiwen
{
public static void main(String[] args)
{
String str=" ";
System.out.println("请输入要判断的字符串(true表示回文字串,false表示非回文字串)");
Scanner input=new Scanner(System.in);
str=input.next();
int i=0;
int j=str.length()-1;
System.out.println(Huiwen.judge(str,i,j));
}
public static boolean judge(String s,int i,int j)
{
if(i>j)
throw new IllegalArgumentException();
if(i==j)
return true;
else
{
return(s.charAt(i)==s.charAt(j)) && judge(s,i+1,j-1);
}
}
}
结果截图:





