C++B树的实现

B树的实现

今天我们就来实现以下B树，B树有什么特点那？我们来列举一下

• 每个非叶子节点中存放若干关键字数据，并且有若干指向儿子节点的指针。指针数目=关键字数目+1
• 根节点有最少1个，最多m-1个关键字，最少2个，最多m个子节点。
• 非根节点最少有m/2，最多m-1个关键字
• 每个节点中的关键字从左到右以非降序排列
• 每个关键字均不小于其左子节点的关键字，不大于其右子节点的所有关键字
• 每个叶子节点都具有相同的深度

B树的节点的增加

我们还是通过1-25个数的增加，来探索一下，B树的增加节点有什么规律，并写出代码。
首先我们定义出来我们B树的结构，如下:

#define DEGREE		3
typedef int KEY_VALUE;

typedef struct _BTREE_NODE
{
    KEY_VALUE* keys;
    struct _BTREE_NODE** Childrens;
    int num;
    int leaf;
}BTREE_NODE,*PBTREE_NODE;

typedef struct _BTREE
{
    BTREE_NODE* root;
    int t;
};

我们来看一下B树1-20个数字的增加的图片
1-5

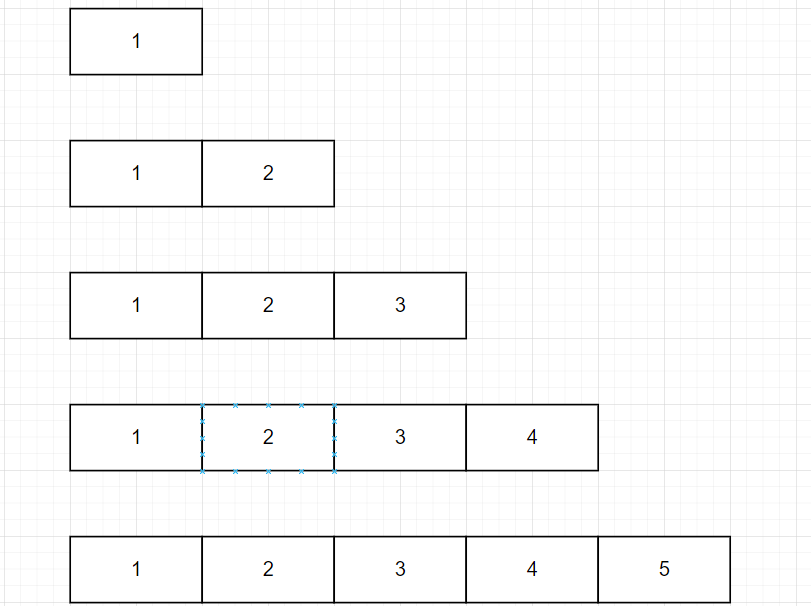
6-10

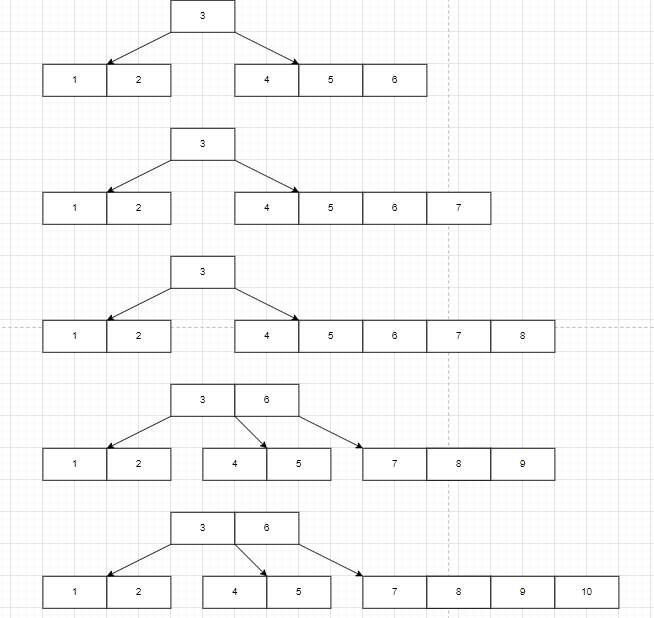
11-15

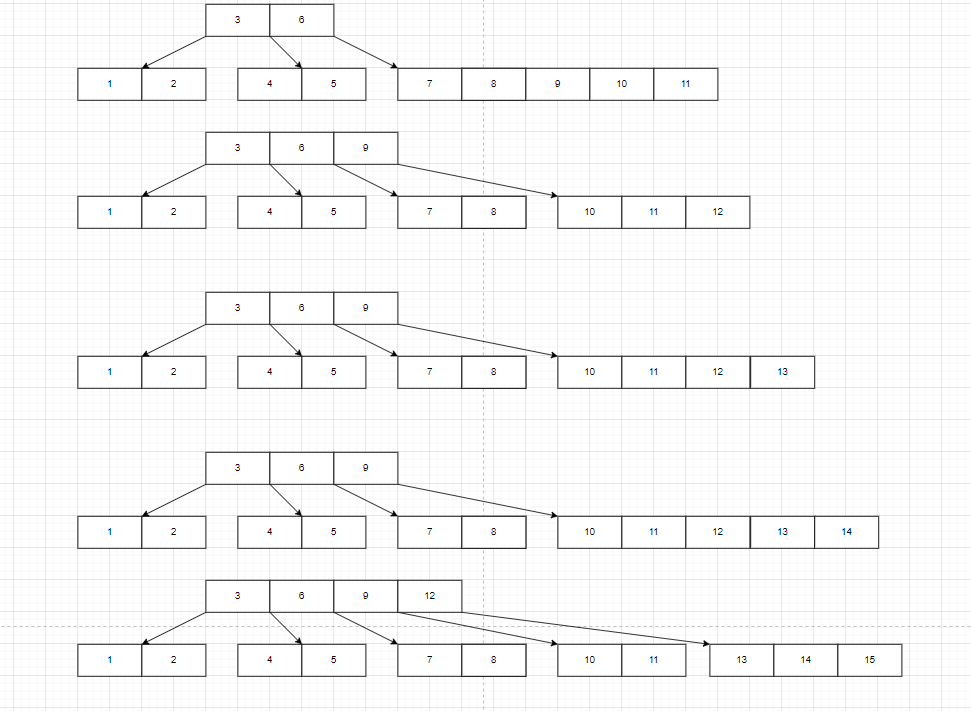
16-20

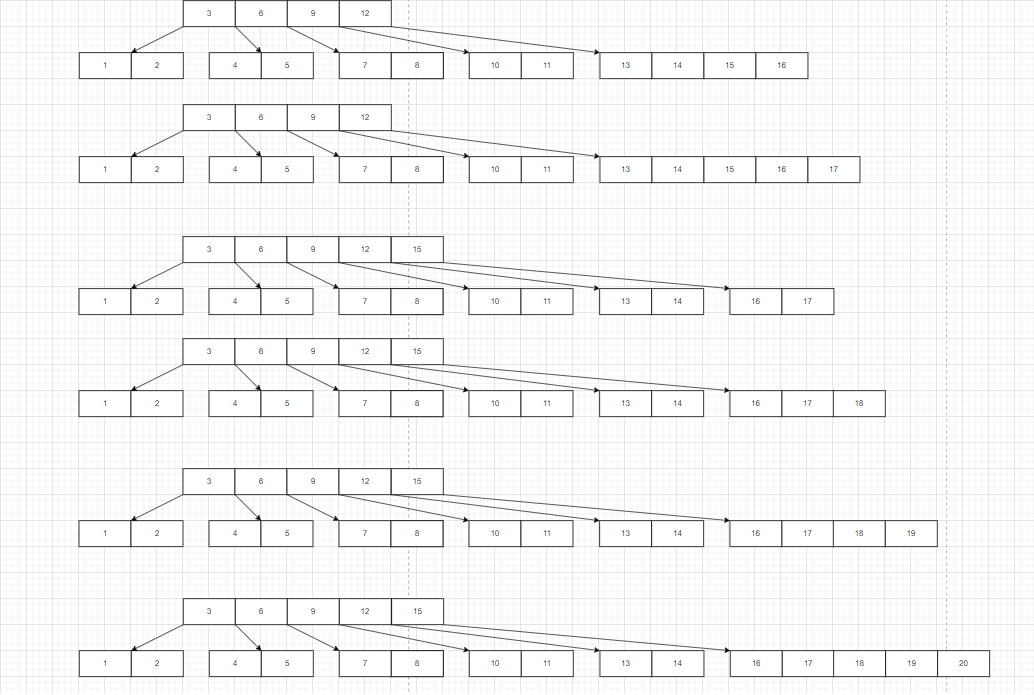
我们首先需要创建一个根节点:

BTREE_NODE* btree_create_node(int t, int leaf) {

    BTREE_NODE* node = (BTREE_NODE*)calloc(1, sizeof(BTREE_NODE));
    if (node == NULL) assert(0);

    node->leaf = leaf;
    node->keys = (KEY_VALUE*)calloc(1, (2 * t - 1) * sizeof(KEY_VALUE));
    node->Childrens = (BTREE_NODE**)calloc(1, (2 * t) * sizeof(BTREE_NODE*));
    node->num = 0;

    return node;
}
//创建根节点
void btree_create(BTREE*T,int t)
{
    T->t = t;
    PBTREE_NODE x = btree_create_node(t, 1);
    T->root = x;
}

现在就写一下我们插入的代码

BTREE_NODE* btree_create_node(int t, int leaf) {

    BTREE_NODE* node = (BTREE_NODE*)calloc(1, sizeof(BTREE_NODE));
    if (node == NULL) assert(0);

    node->leaf = leaf;
    node->keys = (KEY_VALUE*)calloc(1, (2 * t - 1) * sizeof(KEY_VALUE));
    node->Childrens = (BTREE_NODE**)calloc(1, (2 * t) * sizeof(BTREE_NODE*));
    node->num = 0;

    return node;
}
//节点分裂
void btree_split_child(BTREE* T,BTREE_NODE* x,int i)
{
    int t = T->t;

    BTREE_NODE* y = x->Childrens[i];
    BTREE_NODE* z = btree_create_node(t, y->leaf);
    z->num = t - 1;

    int j = 0;
    for (j=0;j<t-1;j++)
    {
        z->keys[j] = y->keys[j + t];
    }
    if (y->leaf==0)
    {
	    for (j=0;j<t;j++)
	    {
            z->Childrens[j] = y->Childrens[j + t];
	    }
    }
    y->num = t - 1;
    for (j=x->num;j>=i+1;j--)
    {
        x->Childrens[j + 1] = x->Childrens[j];
    }
    x->Childrens[i + 1] = z;
    for(j=x->num-1;j>=i;j--)
    {
        x->keys[j + 1] = x->keys[j];
    }
    x->keys[i] = y->keys[t - 1];
    x->num += 1;
}
//创建节点
void btree_create(BTREE*T,int t)
{
    T->t = t;
    PBTREE_NODE x = btree_create_node(t, 1);
    T->root = x;
}
void btree_insert_notfull(BTREE*T,BTREE_NODE *x,KEY_VALUE k)
{
	//获取节点数量,从0开始减1
    int i = x->num-1;
    //只有1个叶子节点
	if (x->leaf==1)
	{
		while (i>=0&&x->keys[i]>k)
		{
            x->keys[i + 1] = x->keys[i];
            i--;
		}
        //赋值
        x->keys[i + 1] = k;
        x->num += 1;
	}else
	{
       //找到应该插入的叶子节点
        while (i >= 0 && x->keys[i] > k) i--;
        //是否已经满了5个节点
       if (x->Childrens[i+1]->num==((2*T->t))-1)
       {
           btree_split_child(T, x, i + 1);
           if (k>x->keys[i+1])
           {
               i++;
           }
       }

       btree_insert_notfull(T, x->Childrens[i + 1], k);
       
		
	}
}
void btree_insert(BTREE *T ,KEY_VALUE key)
{
   //获取头节点
    BTREE_NODE* r = T->root;
    //如果满节点就要进行这里的操作

    if (r->num==2*T->t-1)
    {
        BTREE_NODE* node = btree_create_node(T->t, 0);
        T->root = node;

        node->Childrens[0] = r;

        btree_split_child(T, node, 0);

        int i = 0;
        if (node->keys[0] < key) i++;
        btree_insert_notfull(T, node->Childrens[i], key);
    }
    else
    {
	    //如果没有满就要进行这里的操作
        btree_insert_notfull(T, r, key);
    }
    
}

B树节点的删除

我们还是看一下是如何删除的示意图，然后再写代码。
这里主要讨论一下删除的几种情况，

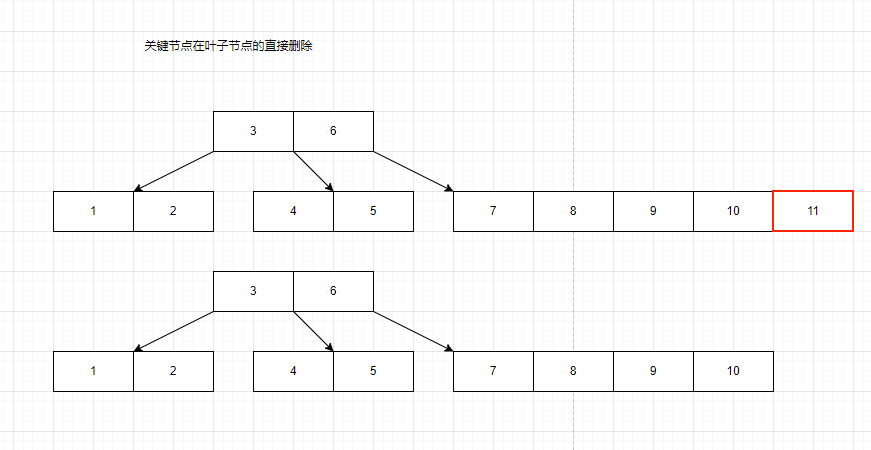
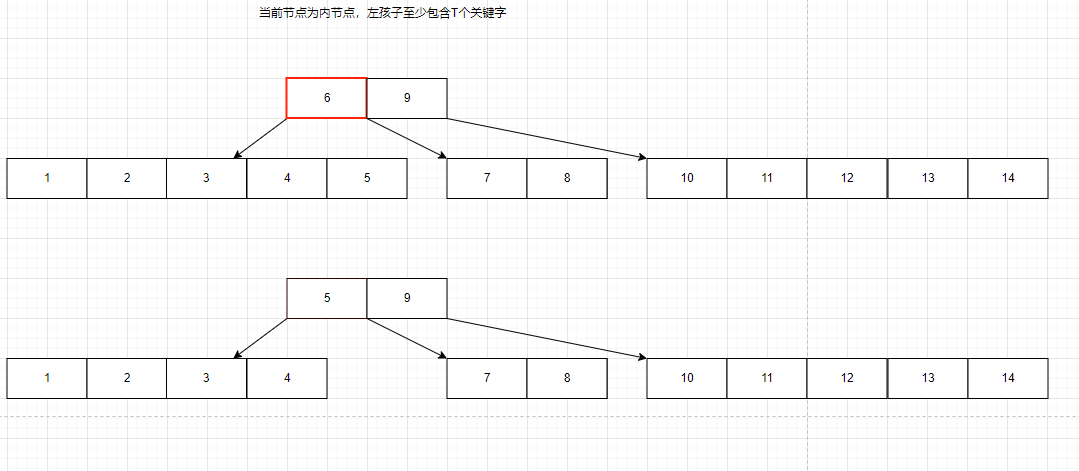
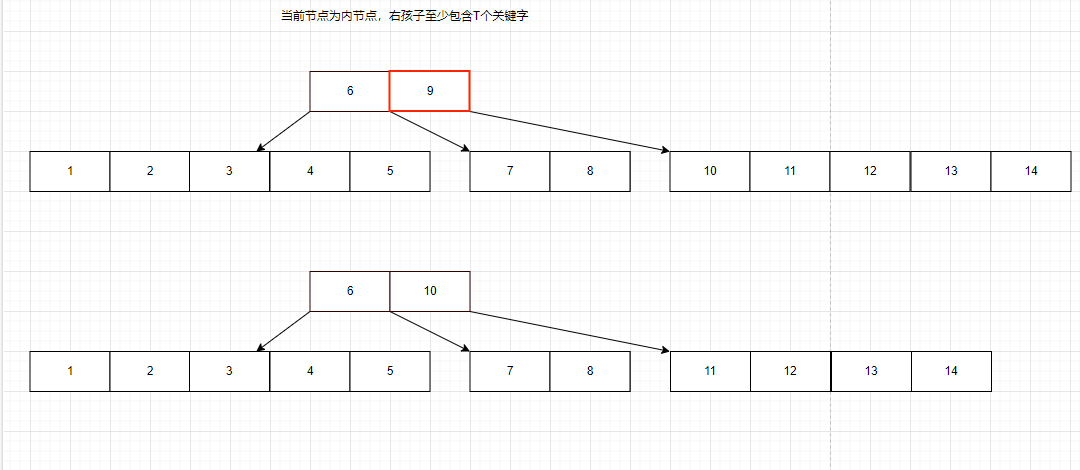
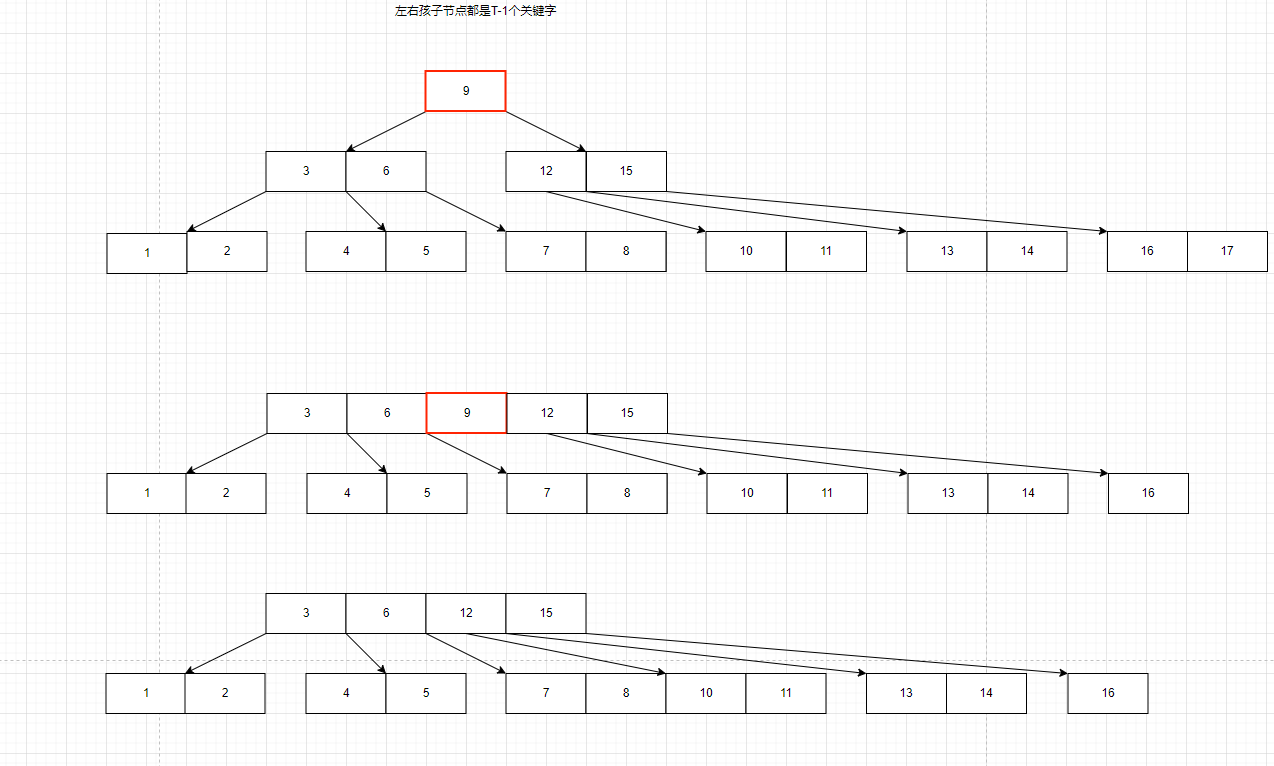
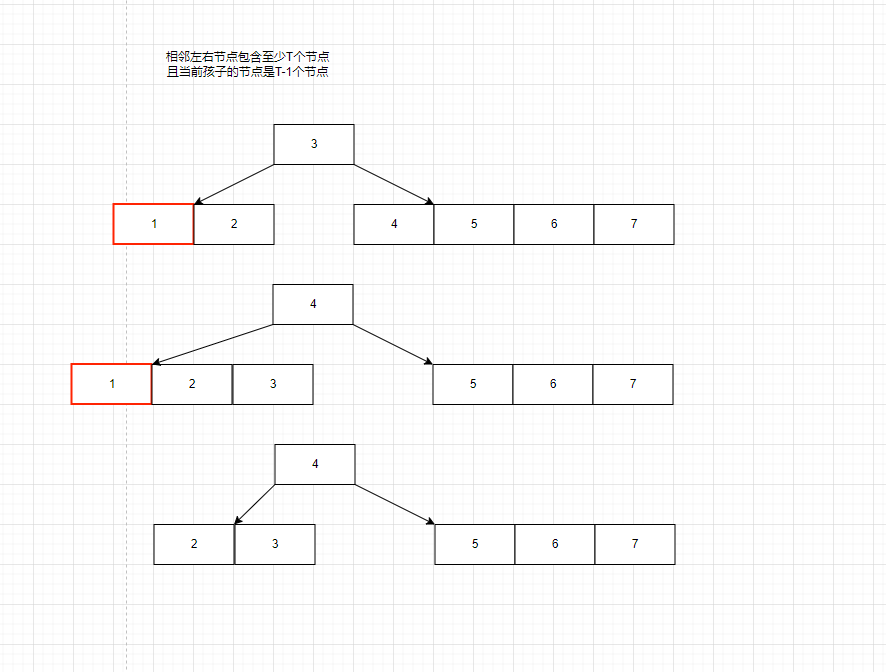
B树删除的代码

//释放节点
void btree_destory_node(BTREE_NODE* node)
{
	if (node == nullptr)
	{
		return;
	}
	free(node->Childrens);
	free(node->keys);
	free(node);
}
void btree_merge(BTREE* T, BTREE_NODE* node, int idx)
{
	BTREE_NODE* left = node->Childrens[idx];
	BTREE_NODE* right = node->Childrens[idx + 1];

	int i = 0;
	left->keys[T->t - 1] = node->keys[idx];
	//开始数据的合并
	for (i = 0; i < T->t - 1; i++)
	{
		left->keys[T->t + 1] = right->keys[i];
	}
	if (!left->leaf)
	{
		for (i = 0; i < T->t; i++)
		{
			left->Childrens[T->t + 1] = right->Childrens[i];
		}
	}
	left->num += T->t;
	//合并完成摧毁节点
	btree_destory_node(right);

	//node
	for (i = idx + 1; i < node->num; i++)
	{
		node->keys[i - 1] = node->keys[i];
		node->Childrens[i] = node->Childrens[i + 1];
	}
	node->Childrens[i + 1] = NULL;
	node->num -= 1;
	if (node->num == 0)
	{
		T->root = left;
		btree_destory_node(node);
	}

}
void btree_delete_key(BTREE* T, BTREE_NODE* node, KEY_VALUE key)
{
	//如果是空节点，直接返回
	if (node == nullptr)
	{
		return;
	}
	int idx = 0, i;
	//获取key所在的位置
	while (idx<node->num && key>node->keys[idx])
	{
		idx++;
	}
	if (idx < node->num && key == node->keys[idx])
	{
		if (node->leaf)
		{
			//如果是叶子节点，直接删除
			for (i = idx; i < node->num - 1; i++)
			{
				node->keys[i] = node->keys[i + 1];
			}
			node->keys[node->num - 1] = 0;
			node->num--;
			//如果是根节点的情况
			if (node->num == 0)
			{
				free(node);
				T->root = nullptr;
			}
			return;
		}//直接删除
		else if (node->Childrens[idx]->num >= T->t)
		{
			BTREE_NODE* left = node->Childrens[idx];
			node->keys[idx] = left->keys[left->num - 1];
			btree_delete_key(T, left, left->keys[left->num - 1]);
		}//直接删除
		else if (node->Childrens[idx + 1]->num >= T->t)
		{
			BTREE_NODE* right = node->Childrens[idx + 1];
			node->keys[idx] = right->keys[0];
			btree_delete_key(T, right, right->keys[0]);

		}
		else {
			//如果都不是,说明是左右孩子节点都是T-1个关键字
			btree_merge(T, node, idx);
			btree_delete_key(T, node->Childrens[idx], key);
		}
	}
	else
	{
		BTREE_NODE* child = node->Childrens[idx];
		if (child == NULL)
		{
			printf("Can\'t del key=%d\n", key);
			return;
		}//子节点的数目刚好等于2
		if (child->num == T->t - 1)
		{
			BTREE_NODE* left = nullptr;
			BTREE_NODE* right = nullptr;
			if (idx - 1 >= 0)
			{
				left = node->Childrens[idx - 1];
			}
			if (idx + 1 <= node->num)
			{
				right = node->Childrens[idx + 1];
			}
			//如果左右节点任何一个都可以借用节点
			if ((left && left->num >= T->t) || (right && right->num >= T->t))
			{
				int richR = 0;
				if (right)
				{
					richR = 1;
				}
				if (left && right)
				{
					richR = (right->num > left->num) ? 1 : 0;
				}
				//从右借用节点
				if (right && right->num >= T->t && richR)
				{
					child->keys[child->num] = node->keys[idx];
					child->Childrens[child->num + 1] = right->Childrens[0];
					child->num++;
					node->keys[idx] = right->keys[0];
					//调整右边的节点
					for (i = 0; i < right->num - 1; i++)
					{
						right->keys[i] = right->keys[i + 1];
						right->Childrens[i] = right->Childrens[i + 1];
					}

					right->keys[right->num - 1] = 0;
					right->Childrens[right->num - 1] = right->Childrens[right->num];
					right->Childrens[right->num] = NULL;
					right->num--;
				}
				else
				{
					//从左借节点
					for (i = child->num; i > 0; i--)
					{
						child->keys[i] = child->keys[i - 1];
						child->Childrens[i + 1] = child->Childrens[i];
					}
					child->Childrens[1] = child->Childrens[0];
					child->Childrens[0] = left->Childrens[left->num];
					child->keys[0] = node->keys[idx - 1];
					child->num++;

					node->keys[idx - 1] = left->keys[left->num - 1];
					left->keys[left->num - 1] = 0;
					left->Childrens[left->num] = NULL;
					left->num--;
				}
				

			}
			else if ((!left) || (left->num == T->t - 1) && (!right) || (right->num == T->t - 1))
			{
				if (left&&left->num==T->t-1)
				{
					btree_merge(T, node, idx - 1);
					child = left;
				}else if(right&&right->num==T->t-1)
				{
					btree_merge(T, node, idx);
				}
			}
			btree_delete_key(T, child, key);
		}
	}

}
int btree_delete(BTREE* T, KEY_VALUE key)
{
	if (!T->root)
	{
		return -1;
	}
	btree_delete_key(T, T->root, key);
	return 0;
}

推荐一个零声学院免费教程，个人觉得老师讲得不错，
分享给大家：[Linux，Nginx，ZeroMQ，MySQL，Redis，
fastdfs，MongoDB，ZK，流媒体，CDN，P2P，K8S，Docker，
TCP/IP，协程，DPDK等技术内容，点击立即学习:
服务器
音视频
dpdk
Linux内核