20221209-卷积计算演示

卷积这个概念，从字面上看比较抽象，加以公式和原理，理解起来也是比较复杂。
卷积是一种计算，其中包括两个字：“卷”和“积”。从”积“字可以猜测，计算过程中应该会涉及到乘法计算。“积”字前面有个“卷”字作为修饰，可以推测卷积中的乘法计算，不是普通的乘法计算，是被某种计算规则所约束的乘法计算。
接下来的内容，不是从公式和概念原理的角度进行解释，而是通过具体计算过程的演示，达到快速掌握卷积计算规则的目的。

1 一维

输入x:　[ 1　2　3 ]
输入y:　[ 4　5　6 ]
z = conv(x, y)
输出z:　[ 4　13　28　27　18 ]
计算过程如下图所示。

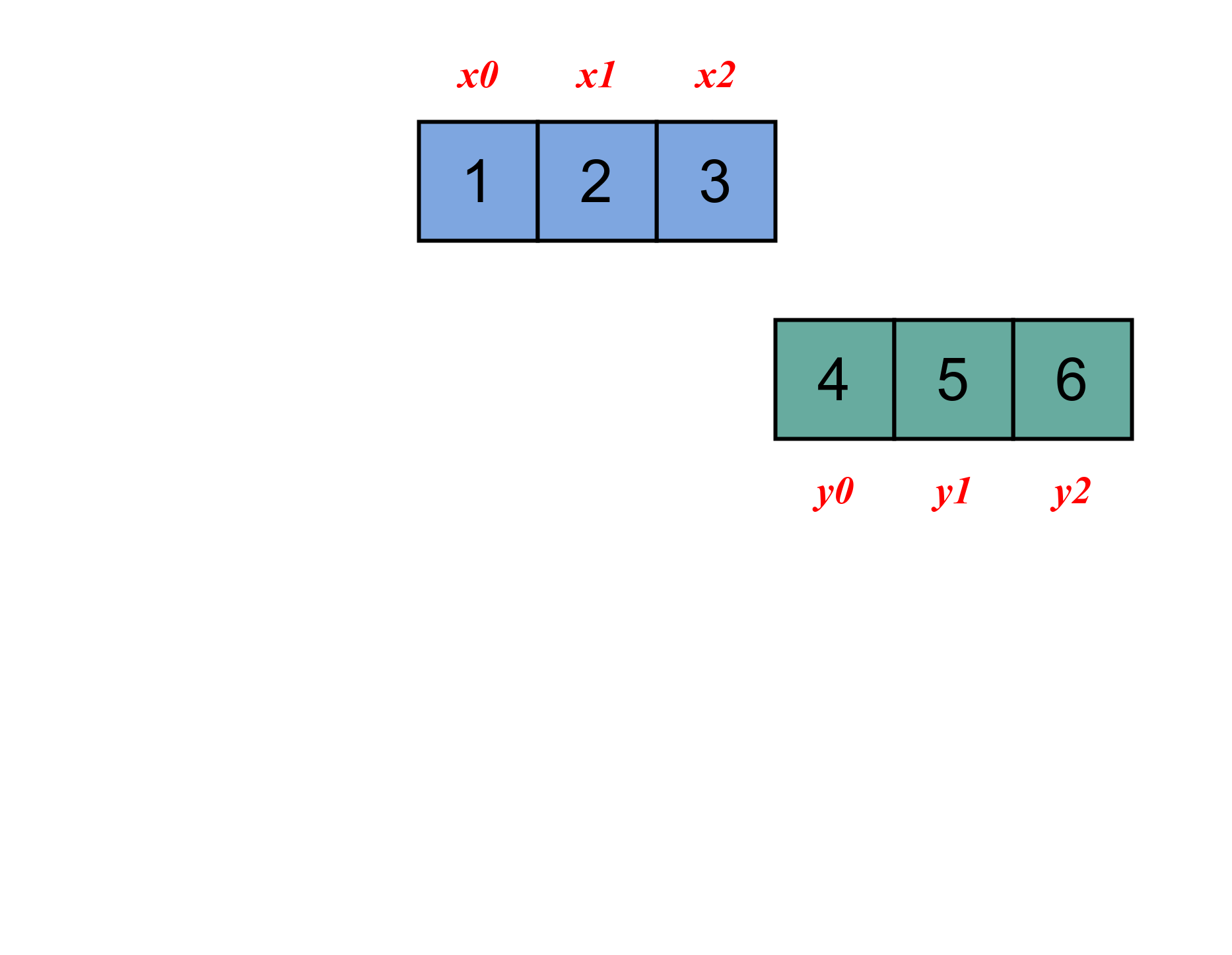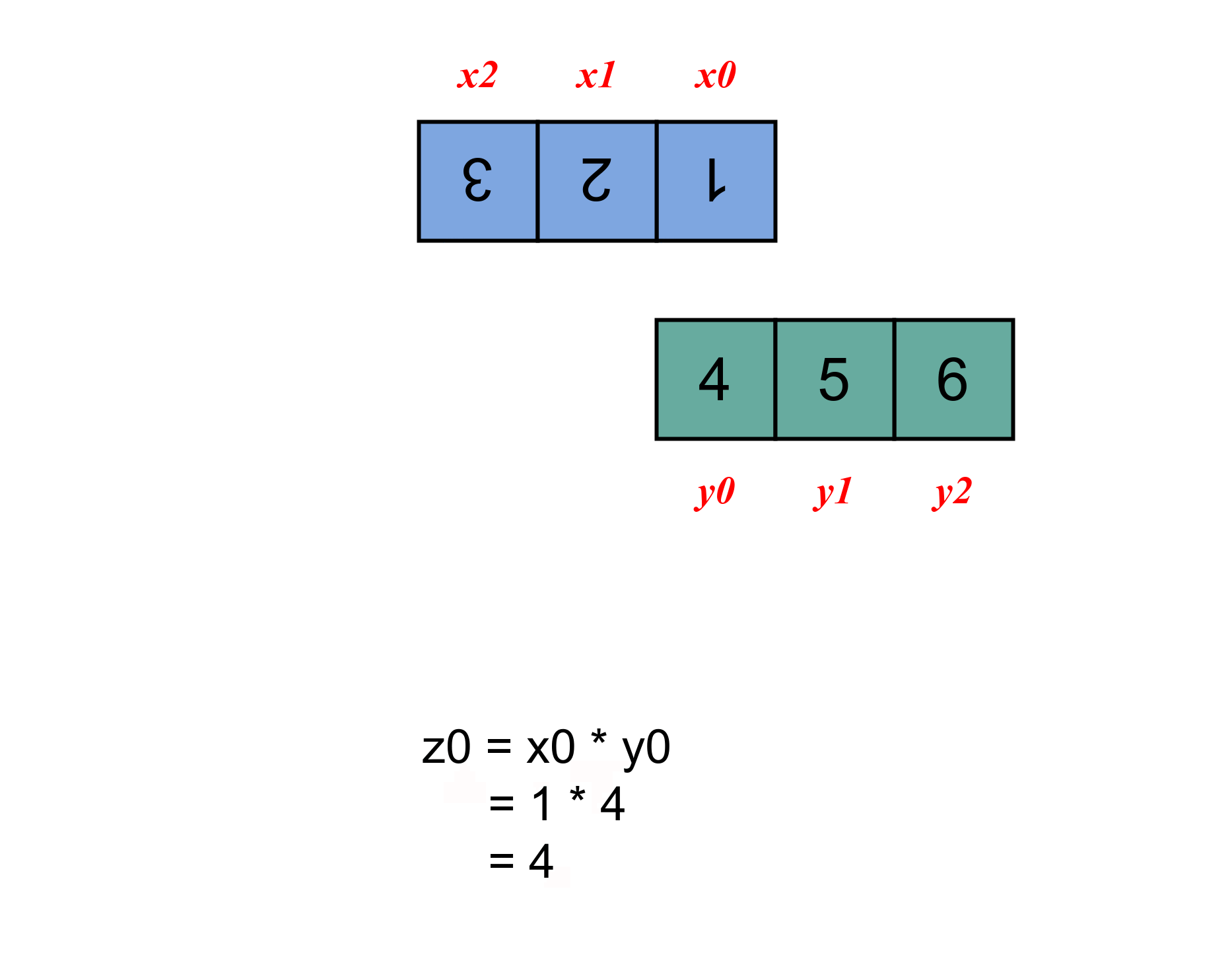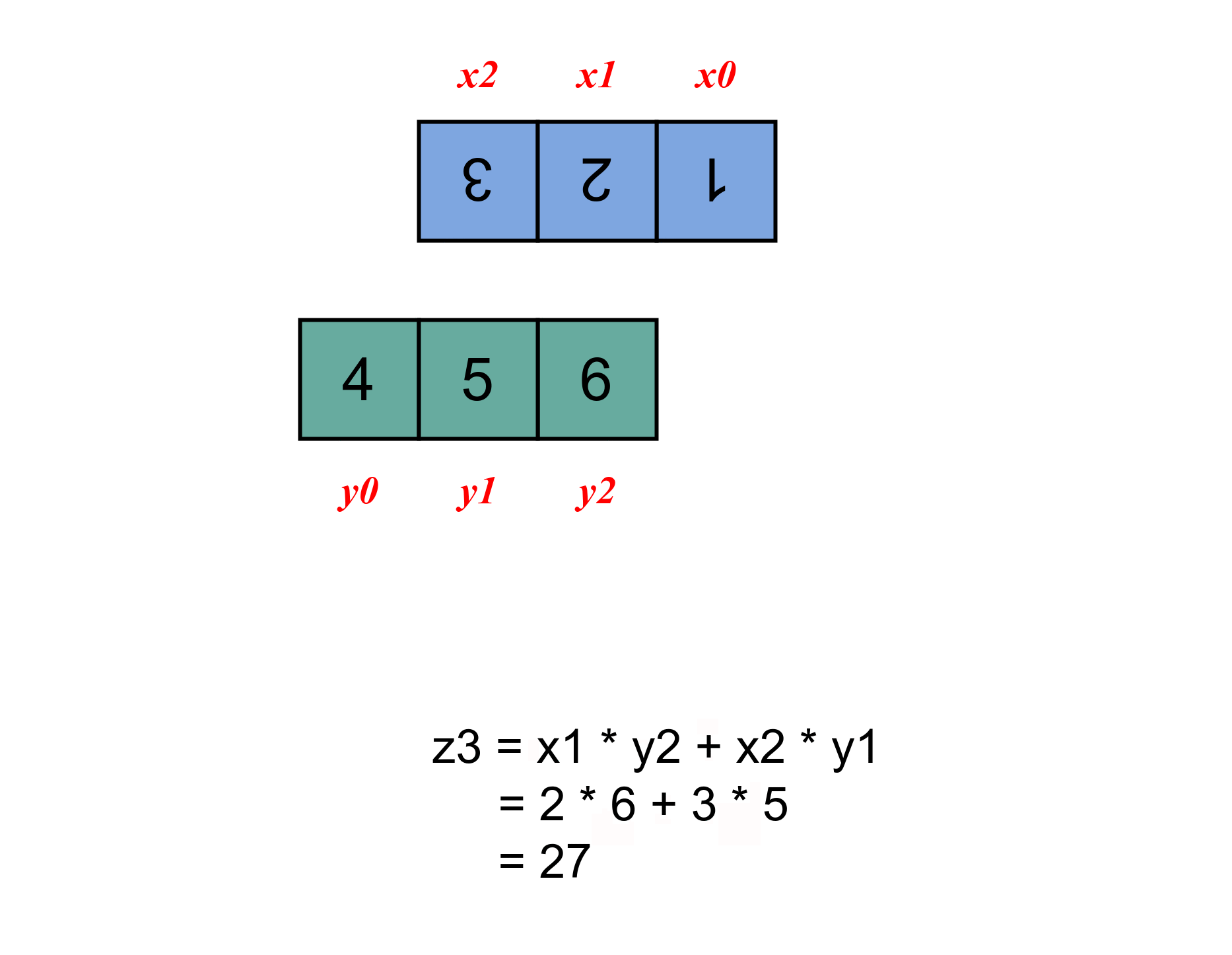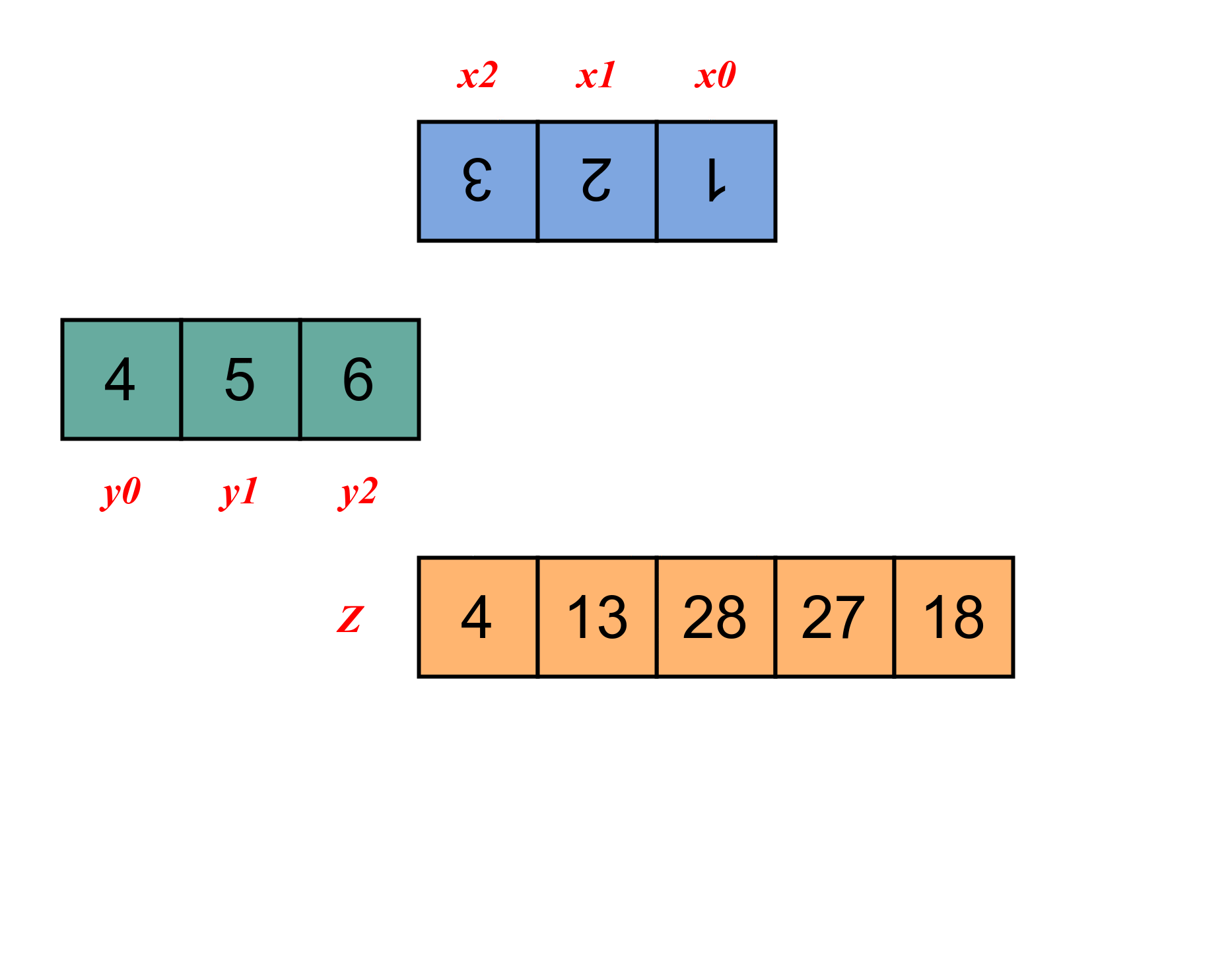
2 二维

输入x:
[   1　2
　3　4 ]
输入y:
[   1　2
　3　4 ]
z = conv(x, y)
输出z:
[   1　  4　  4
　6　20　16
　9　24　16 ]

在一维卷积的基础上，观察二维卷积的计算过程。

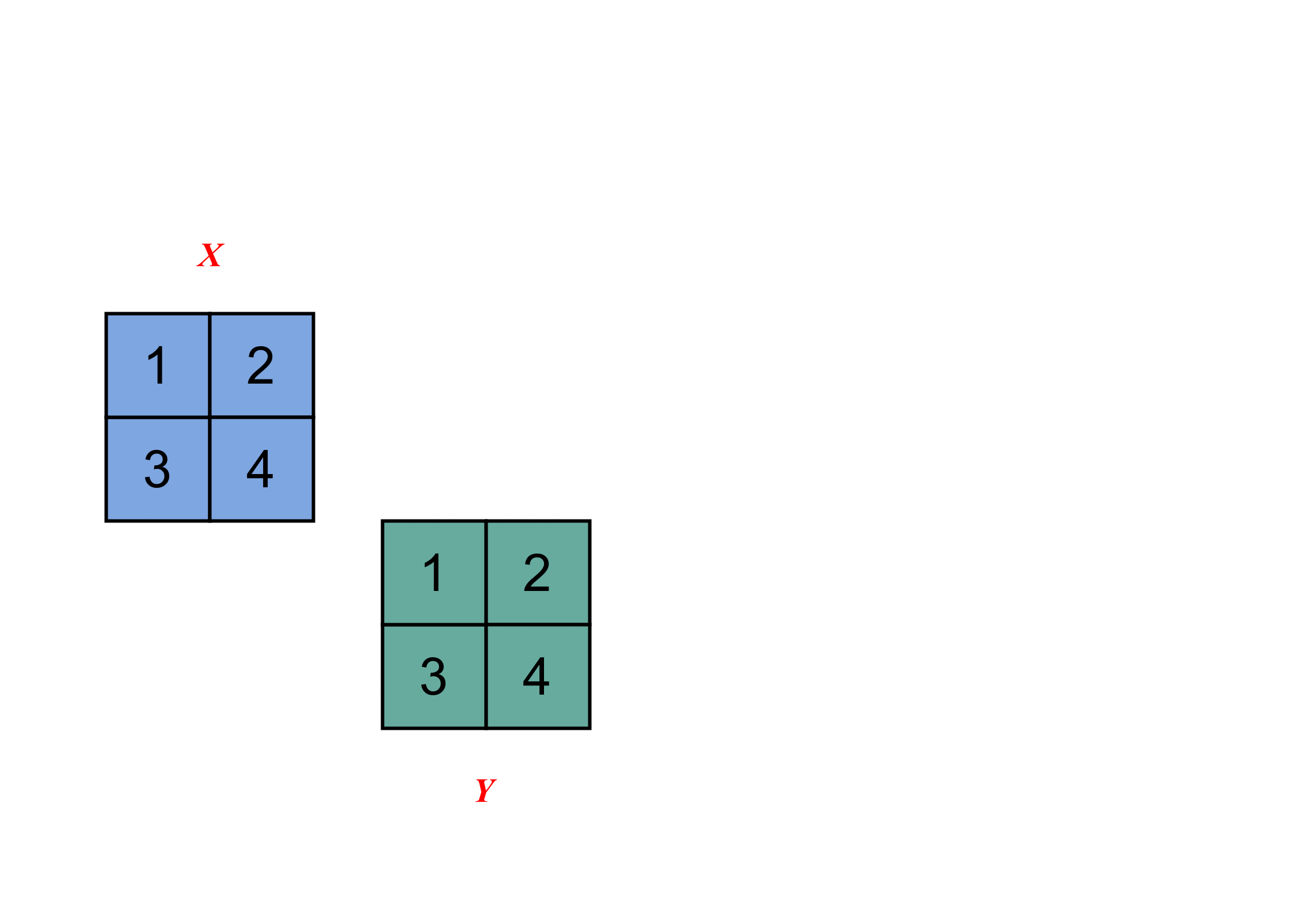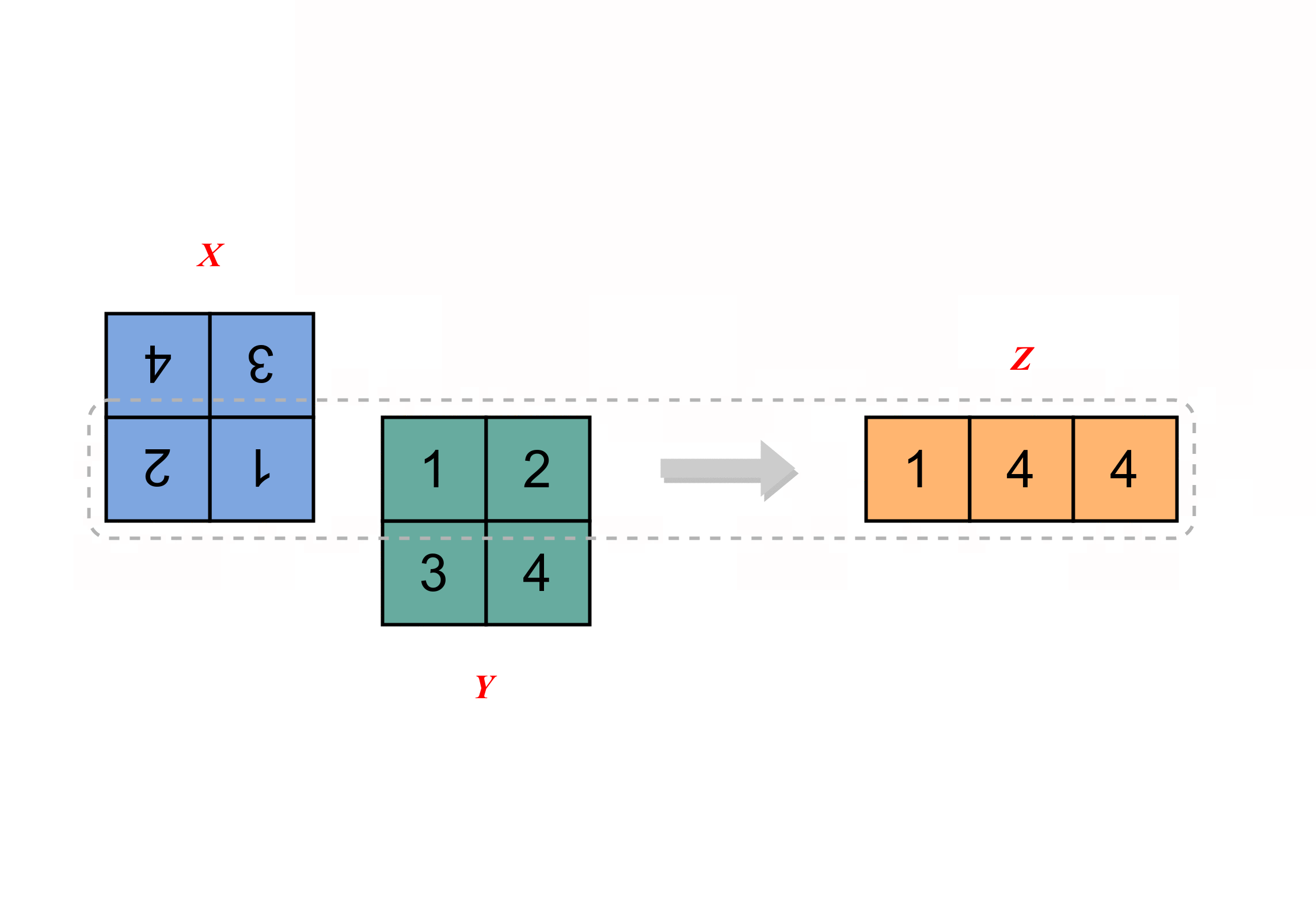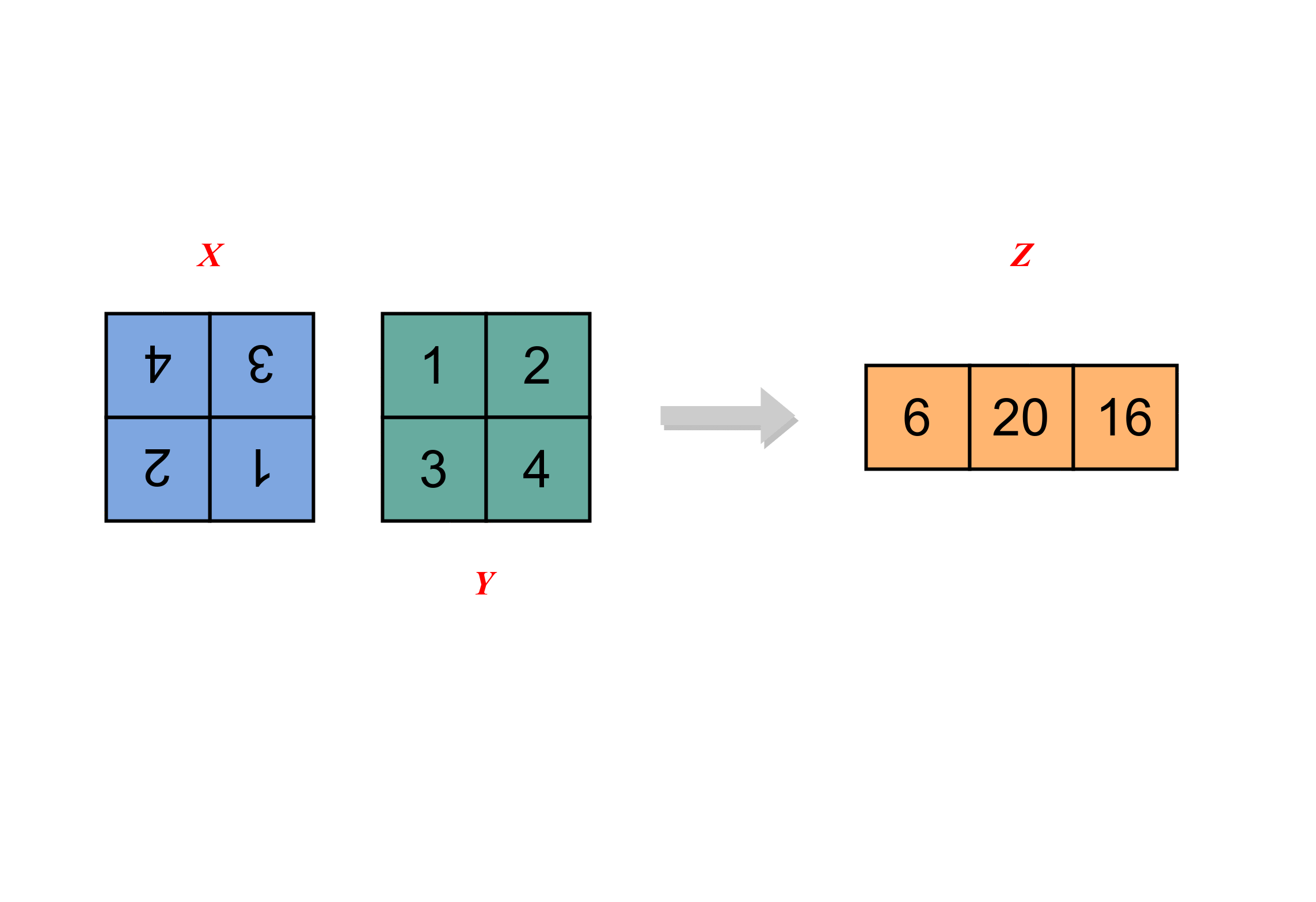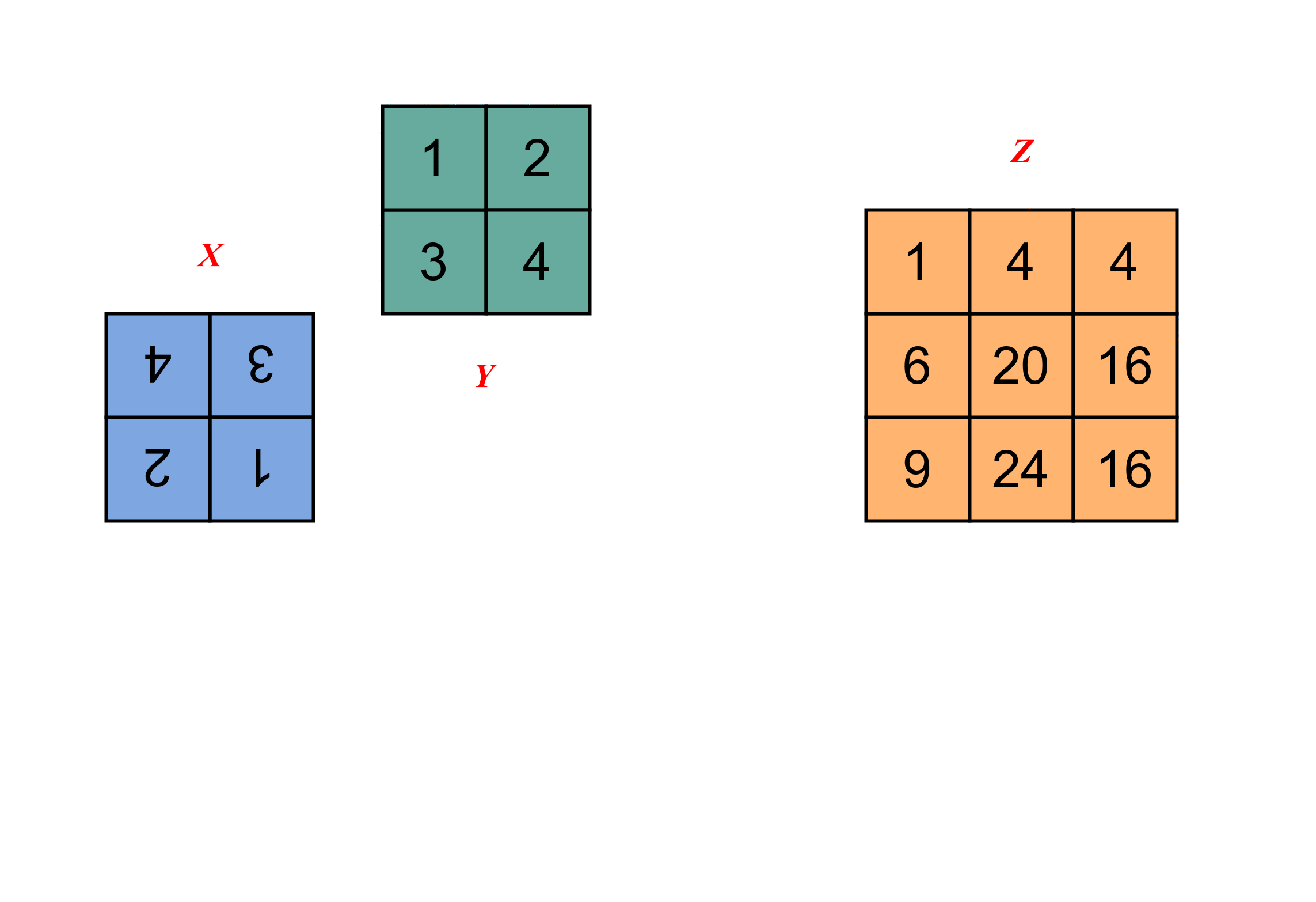
3 多维（三维及以上）

输入x:
[   1　2
　3　4

　5　6
　7　8 ]
输入y:
[   1　2
　3　4

　5　6
　7　8 ]
z = conv(x, y)
输出z:
[     1　　    4　　   4
　  6　　  20　　 16
　  9　　  24　　 16

　10　　  32　　 24
　44　　120　　 80
　42　　104　　 64

　25　　  60　　 36
　70　　164　　 96
　49　　112　　 64 ]
在二维卷积的基础上，观察三维卷积的计算过程。由三维可扩展至更高维度。

总结

通过对一维、二维以及多维卷积计算过程的观察，可以看到，输入x先进行反转，然后滑动y。在滑动过程中，x和y相对应的数据进行乘法计算，得到一组数据，作为输出数据的一部分。滑动结束后，整个卷积计算完成。
卷积计算，就是先反转，再滑动相乘。

拓展

下图是典型的神经网络中的二维卷积计算的示意图。

需要注意的是，神经网络中的卷积和上文中提到的卷积（即基础数学卷积）还是有所差异的。
基础卷积的思路和规则比较简单，即滑动相乘，而且也没什么具体的目的，只是两个输入做计算，得到一个输出。
而神经网络中的卷积的规则和参数就比较多了，重要的一些参数包括权重、偏置、填充、步长等，明显要比基础卷积复杂一些。更关键的是，神经网络中的卷积具有明确的目的和用途，用于训练网络、调参数、提取图像特征等。
如果要做一个类比，一段连续的存储空间，可以朴素地作为一个数组，加以限制条件、更丰富的属性和参数、专门的使用场景，可以得到栈或队列等更复杂的数据结构。