前中后序的非递归实现与理解

根据自己对于对于遍历的理解

前序遍历：中左右

中序遍历：左中右

后序遍历：左右中

 

 

对于前序和中序，可以只改变一些printf的顺序

所以前中后名称都是针对中间（根）的结点，所以后序遍历是不可以直接移动printf的位置的，因为对于每个结点不能直接出栈，出栈输出的时候需要判断2点

1.这个节点有没有右子树（如果没有就遍历他的左子树）

2.这个节点有没有被访问过（如果被访问过说明他的右子树已经遍历完了，可以直接输出）

 

1. void NL_Order(BinTree BST)
   {//后序遍历的思路是：左子树走到了尽头之后，往右子树走，先将右子树输出之后再输出左子树，再输出根节点
       BinTree cur = BST, pre = NULL;
       Stack S; S.top = 0;
       while (cur || !IsEmpty(S))
       {
           if (cur)
           {
               PushStack(S, cur);
               cur = cur->Lchild;//相比起老师给的范例，少了一层循环，将左子树的都无脑压入
           }
           else
           {
               GetTop(S, cur);//获取栈顶（要先进行判断）
               if (cur->Rchild&&cur->Rchild!=pre)    //这是不出栈的，满足了两个条件：①有右结点②没有访问过
               {
                   cur = cur->Rchild;                //往右边遍历
               }
               else
               {
                   PopStack(S, cur);              //满足出栈条件的
                   cout<<cur->data;
                   pre = cur;                     //记录一下当下访问的这个结点，针对的是右边的叶子，下一轮循环访问栈将是它的根，记录已经输出                     右边，确保下一轮循环它的根节点可以输出（即标记已访问）
                   cur = NULL;//避免把当前当前已经访问过结点入栈（针对第一个if）
               }
           }
       }
   }

    

 

---

---

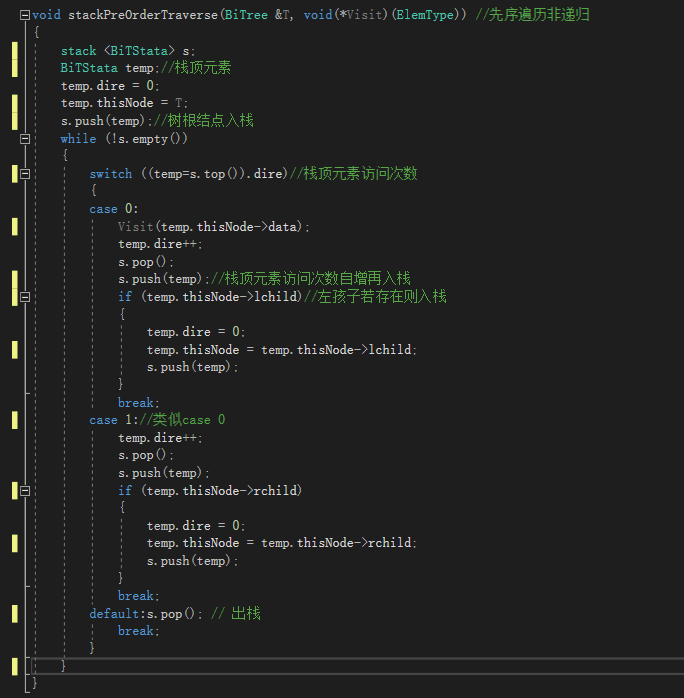
这是同学的解法，觉得很有新意，也更加便于理解栈和递归之间的关系

思想：对于每个结点的访问在递归中有三次，第一次是用其来访问左孩子，第二次是用其来访问右孩子，最后一次是跳出前面两个递归之后回归本层递归，所以依据上述先序、中序、后序的理解，区别就在于第几次访问这个栈的结点

引入一个元素记录访问的次数