二分答案

 

这是一个对二分答案的总结

首先明确的概念是：二分查找虽然是在中点处截取，但是随着截取的越来越精细，是可以确定把答案落在一个具体值身上的

根据二分查找的这个特性，可以快速的在可枚举的数据中进行定位

使用二分答案的条件：

1.可枚举

2.序列呈现递增的形态（这也契合二分查找的要求）

第一类题目：每个节点都固定，找最小的最大值

下面上例子!

 

18725 宇宙迁跃

 

时间限制:1000MS  代码长度限制:10KB
提交次数:0 通过次数:0

 

题型: 编程题   语言: 不限定

 

 

 

Description

 

在基地的科学家发明“透镜”之后，宇宙航行变得更加效率。
作为基地元首的的代理人，你需要在K天内乘坐飞船到达首都川陀。
飞船可以花费一天时间，通过迁跃从一个星系到达另一个星系，但绝不能迁跃到星系之间，那样不但会遇到一些自然危险，也可能永远迷失。
我们把基地至川陀间星系的坐标看成是一个线性序列，例如a星系坐标是10，b星系坐标是15，那么飞船必须具备不小于5的迁跃能力才能从a航行至b。
基地坐标为0，请你根据基地至川陀间的N个星系坐标，计算飞船的迁跃能力至少为多大，才能在K天内（包含K天）到达川陀。

输入格式

第一行两个整数N和K。（1=<N<=10000，1=<K<=10000）
第二行N个整数，表示N个星系的坐标ai，题目确保坐标由小到大排列。（0=<ai<=100000）

输出格式

仅一行,飞船的最小迁跃能力。

 

 

输入样例

 

5 2
1 4 6 10 19

 

 

输出样例

 

10

 

 

提示

 

样例说明：川陀的坐标为最后一个值19。
飞船的迁跃能力至少为10，才能在2天内到达川陀。

 

对这个例子的分析：

用常规思路来思考：从1开始枚举，每个节点，每个都试探能不能成功飞行，这是OK，而且枚举的过程也是从1开始不断增大的

所以我们在main函数里面 通过二分查找在茫茫的范围内通过二分查找来定位最终的答案

ps：总有一个最终的答案ans这是一个临界值，比这个答案小一点的，飞船飞不过去，比这个答案大一点的，飞船都可以飞的过去，所以称之为至少！

main函数里面是常规的二分模板                             check 函数是判断是对mid的判断

如何构造check来进行判断？？？

check（int mid）     //由于要判断，满足的条件有两个：1.飞船可以成功跃迁（如果都跳不过去，那换一个更大的试一下，所以反馈回去，应该是定位到折半查找的左半段）

                                                                                           2.天数不会超过要求的值（这里要求至少，那肯定是把给定的天数都用掉，才可能尽可能的小），这个用一个计数器

{

       跃迁判定：1.相邻点都跳不过去，太菜了，还是找一个更大的吧，直接return 0;

                         2.相邻点可以跳过去，那就一直i++,直到在某个点卡住了（那还是可以找落脚点的，大不了一个个格子跳）

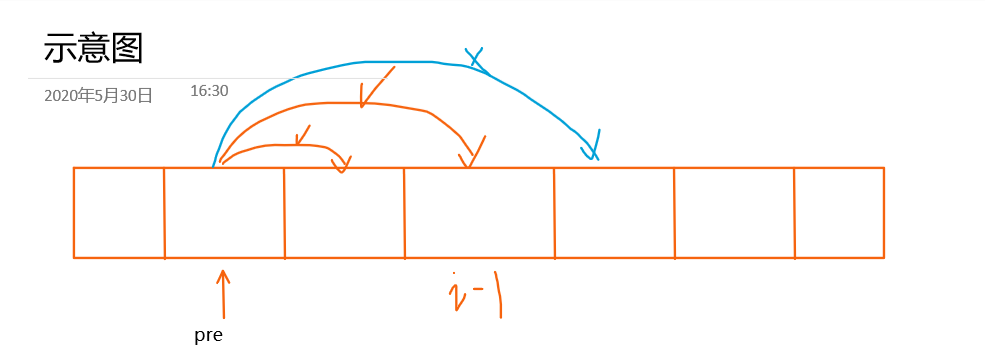
                             由于是用for来进行循环的，能够走到这一步，说明上一个点是可以跳过去的，就如下图所示，此时要做两件事情

                                  ①把a[i-1]设置为落脚点,更新落脚点的位置pre=a[i-1]

                                  ②记录跳跃次数 c++;

！！！！！！！！！！这里有一个非常非常非常容易错的地方，跳跃次数的更新，是当某个点被卡住的时候才会更新，试想一下，现在的跳跃能力超级无敌强，那检测到最后一个格子，他都不会被卡住，那记录的跳跃次数将为0，也就是说，当跳跃能力很强的时候，最后一个点是不会被记录的，所以要人为的在检测的最后，把跳跃次数加一次（最后一跳）

 

 

 

 

}

上代码

#include<iostream>
using namespace std;
int a[10005],n,k;
int check(int x)
{
    int i=1,c=0,pre=0;
    while(i<=n&&c<=k)
    {
      if(x<a[i]-a[i-1])return 0;//如果都不支持相邻点之间的条约，那么不用再考虑
      if(a[i]-pre>x)//如果现在到这个点跳不过去了，那就跳到前一个点（因为是逐个循环，前一个点肯定可以到），那么从这轮开始pre就是a[i-1] 
      {
          pre=a[i-1];
          c++;//记录跳跃的次数,需要多跳一次了 
       } 
          else i++;
    }
    c++;  //前面测试了可行性，但是不会记录最后一跳,补最后一天!! 
    return c<=k;
}
int main()
{
    ios::sync_with_stdio(0),cin.tie(0);
    int i,j,k;
    cin>>n>>k;//记录站点的数量 天数 
    for(i=1;i<=n;i++)  //读入数据 
        cin>>a[i];
    int l=1,r=1000000,mid,ans;
    while(l<=r)
    {
        mid=(l+r)/2;//这是二进制位往左移动一格，意思就是/2 
        if(check(mid))
        {
            ans=mid;
            r=mid-1;
         } 
         else l=mid+1;
    }  //在这个部分采用二分搜索的方法，在茫茫的数字中寻找那个临界点 
    cout<<ans;
    return 0;
}

 第二类题目：可以新增节点，以确定最小的最大值

上题目！

18729 太空航站

时间限制:1000MS  代码长度限制:10KB
提交次数:0 通过次数:0

题型: 编程题   语言: 不限定

 

Description

市政府在基地一和基地二之间修建了n个太空航站，其中基地一为第1个航站，基地二为第n个航站,其他航站在两个基地之间。
我们把相邻航站的距离定义为“空间差”，显然飞船的续航能力必须大于等于这个空间差才能在两个航站间航行。
把所有相邻航站间空间差的最大值定义为“空间极差”，如果一艘飞船想从基地一航行至基地二，
那么它的续航能力必须大于等于“空间极差”，这样看能满足航行条件的飞船太少了。
现在市政府打算在基地一和基地二之间新增最多K个太空航站，让尽可能多的飞船可以在基地一和基地二之间航行。
简单说就是让所有航站间的“空间极差”尽可能地小。

输入格式

第一行为两个整数n和k。（2=<n<=100000）,（1=<k<=100）
第二行，n个正整数a1....an。(a1<=a2<=a3......<=an) 

输出格式

仅一行，新增最多K个太空航站后，“空间极差”的最小值。

 

输入样例

2 1
0 105

 

输出样例

53

 

提示

新的空间站建设在坐标52或53可以得到最小空间极差。

 

这一种题目的思路其实和第一类应该是一样的，这是一个问题的两种问法，但是解法有些不一样

第一类问题的限制条件是：跳几轮

第二类问题的限制条件是：节点的个数

但实际上：跳的每一轮，中间那些节点可以忽略（相当于不必要的站点），所以问题就转变成了，在每一轮的跳跃中，什么是有必要的站点呢？

solution：有必要的站点——在给出的极差下跳不过去，就需要一个跳板——映射问题一：在给出的极差下这个点跳不到，那就落在上一个点

所以在check函数中考虑的问题就是

{

1、现在给出的极差在节点之间跳动足够吗

①if足够 检测下一个下一段距离——>if全部足够 可以试一下更小的极差

②else if 不足够  增加节点作为跳板，记录增加的跳板数

2、如何才算是跳板不足够

      判断条件    距离/极差   如果大于1那就说明距离比极差还要大   //ps：1.用除法的原因是因为除法可以顺便知道在这个极差条件下要增加几个节点，一般x段意味着要增加x-1个节点

                                                                                                                    2.注意在计算机中除法都是整除，所以可以检测一下有没有小数点，如果有小数点，说明要增加x个节点

}

看代码！！

#include<iostream>
#include<algorithm>
using namespace std;
int n,k;
int a[10005];
int check(int x)
{
    int c=0;//记录插入的站点
    int i;
    for(i=2;i<=n&&c<=k;i++)
    {
        int piece=(a[i]-a[i-1])/x;
        int sum=piece*x;
        int truth=a[i]-a[i-1];
         if(piece>1&&sum==truth)//现在极差太大了，需要插入，而且这是没有小数点的情况
         c+=piece-1;//画图可知道n段需要插入n-1个节点
         else if(piece>=1&&sum<truth)
         c+=piece;//实际上还要多一点点，需要多一个救济跳板 
     } 
     return c<=k;
}
int main()
{
    ios::sync_with_stdio(false);
    int best;int mid;int maxgap=0;
    cin>>n>>k;//原来有N个空间站，现在加入K个 
//    int a[n+1];
    for(int i=1;i<=n;i++)
      {
      cin>>a[i];//录入空间站的坐标
      maxgap=max(maxgap,a[i]-a[i-1]);//找出现在的坐标情况下的最大极差 
      }
     best=maxgap;//在不插入的情况下，最大极差就这样 
     int left=0,right=maxgap;
     while(left<=right)
     {
         mid=(left+right)>>1;//二进制数往左移动一个格子，相当于除以2
        if(check(mid)) 
          {
              best=mid;
             right=mid-1;//说明这个极差太大了，可以再尝试小于一点的 
          }
        else 
        {
        left=mid+1;//说明这个极差太小了，现在的空间站不足够给他落点的，在右边找 
      } 
    }
    cout<<best<<endl; 
}