[CF 613 Div.1E] Puzzle Lover

这道题目……感觉细节爆炸级别的多啊……要不是去找人要了代码感觉都要调不出来了

题意

有一个\(2\times N\)的网格，其中每个网格上面都有一个字符，问上下左右走，能够走出多少个给定的字符串\(S\)？答案对\(10^9+7\)取模。
\(1\leq N \leq 2\times 10^3\)

分析

实际上可以发现，这样的路径肯定最多就是长这样的形式：左边一段绕回来的路径，中间一段可以上下跑得路径，右边一段绕回来的路径。

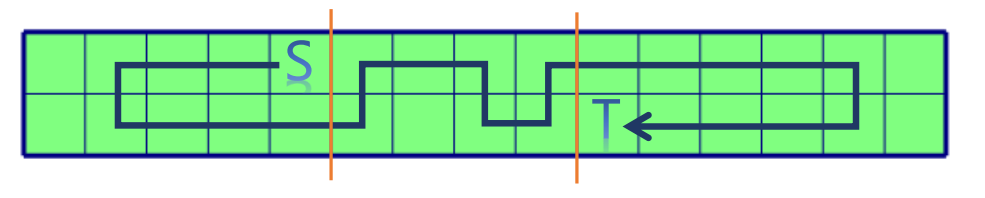
为什么是这样的呢？考虑两边“绕回来”的路径，因为每个节点只能被经过一次，所以必然不能在“绕回去”。那么这个分类正确性就很显然了。
左右两边，相当于是要上下两个长度相等的段合起来匹配，而且肯定是前缀或者后缀这样的，利用哈希即可。
进一步在中间做一个dp，\(f_{i,j,k}\)表示在\(i\)行\(j\)列匹配到串的位置\(k\)，把三段拼起来就好了（实际上是两段，我们考虑可以正着和反着各做一遍，每一次可以同时处理dp与一边的hash，全部算进dp里面，表示从某个点出去，匹配半条路径，也就是一段中间的+一段往回绕的，最后拼起来）。代码里面dp的细节比较多，非常难调……

# include <bits/stdc++.h>
# define re(i,a,b) for (int i=(a);i<(b);++i)
# define rep(i,a,b) for (int i=(a);i<=(b);++i)
# define cl(x) memset(x,0,sizeof(x))
using namespace std;
typedef long long ll;

inline char nc(){
  static char buf[100000],*p1=buf,*p2=buf;
  return p1==p2&&(p2=(p1=buf)+fread(buf,1,100000,stdin),p1==p2)?EOF:*p1++;
}
inline int read(char *s){
  char c=nc(); int len=0;
  for (;!(c>='a' && c<='z');c=nc());
  for (;c>='a' && c<='z';s[++len]=c,c=nc()); s[++len]=0; return len-1;
}
const int P=1e9+7;
const int N=2005;
inline void add(int &x,int y){
  x+=y; if (x>=P) x-=P; 
}
const ll S=31;
const ll MOD=987654321;
ll seed[N];
inline void Pre(int n){
  seed[0]=1;
  rep(i,1,n) seed[i]=seed[i-1]*S%MOD;
}
struct Hash{
  ll h[N];
  inline void make(int n,char *s){
    h[0]=0;
    rep(i,1,n) h[i]=(h[i-1]*S+s[i]-'a')%MOD;
  }
  inline ll cut(int l,int r){
    return (h[r]+MOD-h[l-1]*seed[r-l+1]%MOD)%MOD;
  }
}pre[2],suf[2],ss;

int n,m;
char a[2][N],s[N];
int f[2][N][N];

inline int Solve(int flag){
  int ret=0; cl(f);
  rep(j,1,n){
    f[0][j][0]=f[1][j][0]=1;
    re(i,0,2) rep(k,2,min(n-j+1,m/2))
    if (ss.cut(m-2*k+1,m-k)==pre[i].cut(j,j+k-1) && ss.cut(m-k+1,m)==suf[i^1].cut(n-(j+k-1)+1,n-j+1))
      if (2*k!=m || flag)
        add(ret,f[i][j][m-2*k]);
    re(i,0,2) rep(k,2,min(j,m/2))
    if (ss.cut(k+1,2*k)==pre[i].cut(j-k+1,j) && ss.cut(1,k)==suf[i^1].cut(n-j+1,n-(j-k+1)+1))
      if (2*k!=m || flag)
        add(f[i][j+1][2*k],1);
    re(i,0,2) re(k,0,m)
    if (a[i][j]==s[k+1]){
      add(f[i][j+1][k+1],f[i][j][k]);
      if (k+2<=m && a[i^1][j]==s[k+2])
        add(f[i^1][j+1][k+2],f[i][j][k]);
    }
    re(i,0,2)
      add(ret,f[i][j+1][m]);
  }
  return ret;
}

int main(){
  freopen("string.in","r",stdin);
  freopen("string.out","w",stdout);
  Pre(2000);
  n=read(a[0]); read(a[1]);
  re(i,0,2){
    pre[i].make(n,a[i]);
    reverse(a[i]+1,a[i]+n+1);
    suf[i].make(n,a[i]);
    reverse(a[i]+1,a[i]+n+1);
  }
  m=read(s); ss.make(m,s);
  int Ans=0;
  add(Ans,Solve(1));
  if (m>1){
    reverse(s+1,s+m+1);
    ss.make(m,s);
    add(Ans,Solve(0));
    if (m==2){
      rep(j,1,n) re(i,0,2)
      if (a[i][j]==s[1] && a[i^1][j]==s[2])
        add(Ans,P-1);
    }
  }
  printf("%d\n",Ans);
  return 0;
}