整数规划

整数规划与分配问题

整数规划问题的提出

所谓整数规划：
决策变量要求取整数的线性规划

整数规划数学模型：

\[\max_{}(\min_{}) z = \sum_{j=1}^{n}s_j x_j \\ s.t. \begin{cases} \displaystyle \sum a_{ij}x_j \le b_i \quad (i=1,2,\cdots,m) \\ x_j \ge 0\ 且全部或部分是整数 \end{cases} \]

整数规划问题可以分为以下几种类型：

• 纯整数线性规划：全部决策变量都必须取整数的整数线性规划
• 混合整数规划：只要求一部分决策变量取数值
• 0-1整数规划：要求决策变量取值只能为0或1

---

分枝定界法

分枝定界法是一种隐藏枚举法或部分枚举法，是在枚举法的基础上改进的

原问题的 松弛问题 ：
任何整数规划，凡是放弃某些约束条件（如整数要求）后，所得到的新问题，称为原问题的松弛问题

分枝定界法解题步骤

1. 寻找替代问题并求解
   • 放宽或取消原问题的某些约束条件，找出一个替代问题
   • 替代问题要求：容易求解，且原问题的解集应无一例外地包含在替代问题地解集中
   • 若替代问题无可行解，则原线性规划问题无可行解
   • 如果替代问题的 最优解 是原问题的 可行解，这个解就是原问题的最优解
   • 否则这个解的值是原问题最优解的 上界（求极大值时）或 下界（求极小值时）
2. 分枝与定界
   • 将替代问题分成若干个子问题，对子问题也要求容易求解，且各子问题的解集要包含原问题的解集，对每个问题求最优解
   • 若该解满足原问题的约束，即找到了一个原问题的 可行解
   • 否则该解为所属分枝的边界值（极大极小问题对应上下界）
   • 如果所有子问题的最优解均非原问题的 可行解，则选取其上界最大（求极大值时）或下界最小（求极小值时）的子问题进一步在细分子问题求解。
   • 重复分枝过程，直至找到一个找到一个原问题的可行解为止。
   • 若计算过程中同时出现两个及以上的可行解，则选取其中上界最大（求极大值时）或下界最小（求极小值时）的一个保留
3. 剪枝
   • 将各子问题边界值与保留的可行解的值进行比较，把边界值劣于可行解的分枝剪去
   • 如果除了保留下的可行解外，其余分枝均被剪去，则该可行解就是原问题的最优解
   • 否则，回到分枝与定界，选取边界值最有的一个继续分枝。如果计算过程中又出现新的可行解时，则与原可行解进行比较，保留最优的，并重复上述步骤。

---

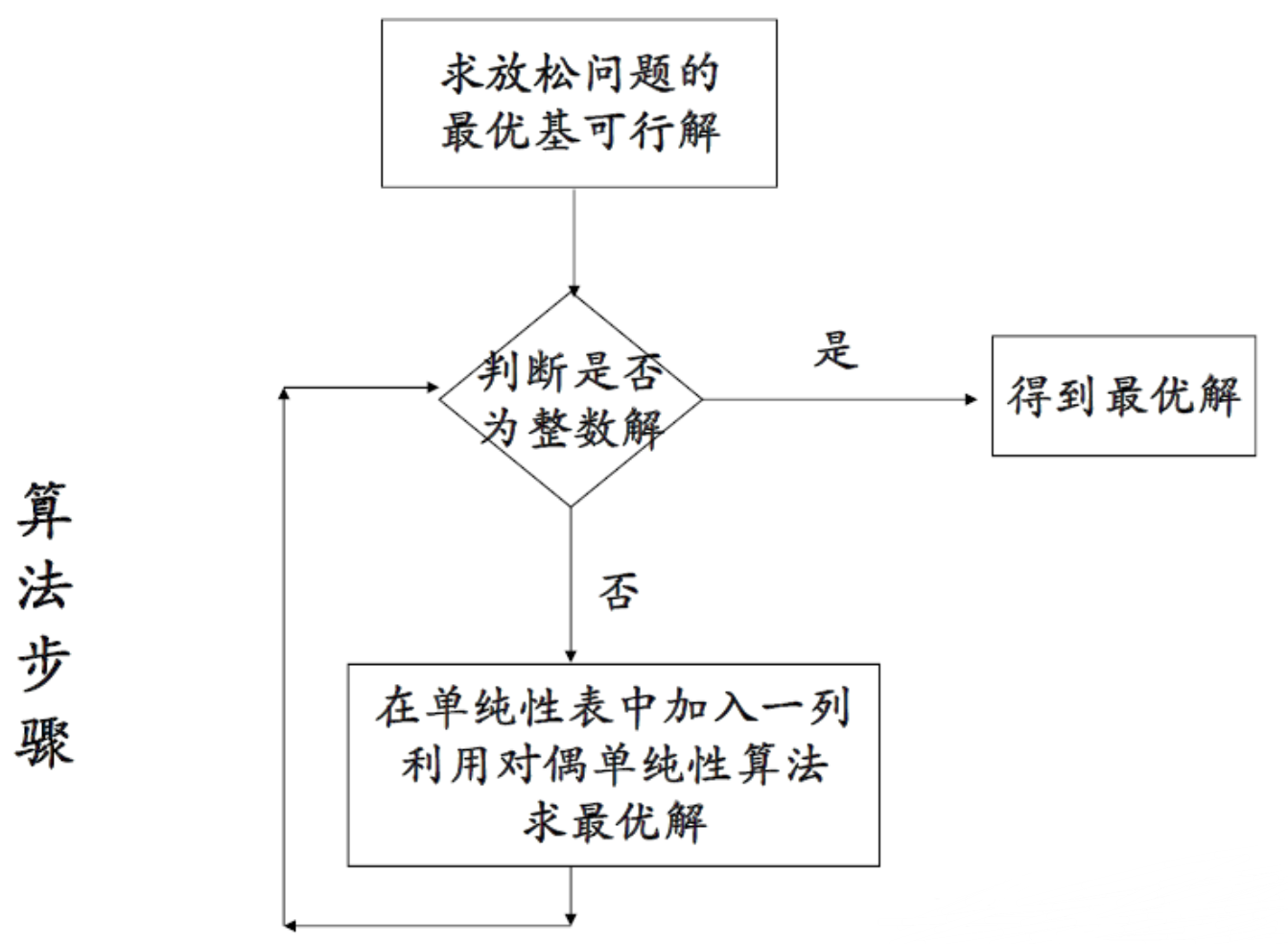
割平面法

基本思想：

在整数规划问题的松弛问题中依次引进线性约束条件（称为割平面），使得问题的可行域逐步缩小。但每次切割只割去问题的部分非整数解，直到问题的目标函数值达到最优的整数点成为缩小后可行域的一个顶点，这样就可以用求解线性规划问题的方法找出这个最优解

割平面法解题思路;

• 不考虑问题中变量的 整数约束条件，得到原问题松弛条件并求解，若该最优解满足整数条件，则该解就是原问题最优解
• 若松弛问题的最优解不满足整数条件，则从该解的非整分量中选取一个，用于构造新的线性约束条件，并将其加入到原松弛问题中形成新的线性规划之后求解。
• 重复上述步骤，直至新的松弛问题求得解满足整数条件为止
• 每次新增加的线性约束条件应满足两个基本性质
  • 已获得的不符合整数要求的线性规划最优解不满足该线性约束条件，从而不可能在以后的解中再出现
  • 凡整数可行解均满足该线性约束条件，故整数最优解始终被保留在每次形成的线性规划可行域中
  

---

分配问题与匈牙利法

分配问题（又称指派问题）：一类特殊的0-1规划问题，可以看成是运输问题的特例
问题描述：

假定有 m 项任务分配给 m 个人去完成，并指定每个人完成其中的一项，每项只交给其中一个人去完成，应如何分配才能使总的效率最高。

指派问题的一般数学模型：

\[\min_{} z = \sum_{i=1}^{m} \sum_{j=1}^{m} c_{ij} x_{ij} \\ s.t. \begin{cases} \displaystyle \sum_{j=1}^{m} x_{ij}=1 \quad (i=1,2,\cdots,m)\\ \displaystyle \sum_{i=1}^{m} x_{ij}=1 \quad (j=1,2,\cdots,m)\\ x_{ij} = 0\ or\ 1 \quad (i=1,2,\cdots,m;j=1,2,\cdots,m) \end{cases} \]

若指派问题的系数矩阵为\((c_{ij})_{m \times m}\)，其最优解为\(x_{ij}(i,j=1,\cdots,m)\)，则其最优解与系数矩阵之间有如下性质：

定理：若从系数矩阵\((c_{ij})_{m \times m}\)的每行（或列）加上或减去一个常数 \(u_i(or\ v_j)\)构成新矩阵 \((c_{ij}^{'})_{m \times m}\)，其中\(c^{'}_{ij}=c_{ij}\pm(u_i+v_j)\)，则新矩阵\((c_{ij}^{'})_{m \times m}\)对应的最优解与原矩阵 \((c_{ij})_{m \times m}\)的最优解 \((x_{ij})_{m\times m}\)相同

匈牙利法

原理：找出一组位于 不同行、不同列 的0元素（称之为独立的0元素），并令其对应的解元素 \(x_{ij} = 1\) ，其他元素 \(x_{ij} = 0\)
算法的关键：寻找独立的零元素

匈牙利法求解步骤：

1. 变换系数矩阵\((c^{'}_{ij})_{m\times m}\)，使其各行各列都出现0元素
   • 对系数矩阵的每行减去该行的最小元素
   • 再对上述得到的新的系数矩阵的每列元素中减去该列的最小元素
2. 进行试指派，求得最优解
   1. 从只有一个0元素的行（列）开始，给这个0元素加圈，记作⭕（其代表对该行所代表的人，只有这一种任务可指派）；之后划去⭕所在列（行）的其它0元素，记作$\times $（其代表该列所代表的任务已指派完毕，不用再考虑其他人了）
   2. 再给剩下的只有一个0元素列（行）的0元素加圈，记作⭕；之后划去⭕所在行的0元素，记作$\times $
   3. 反复1、2两步，直至所有0元素都被标记为止。
   4. 若最少0元素行中零元素的个数至少有2个，则从0元素所在列中最少的始加圈，然后划掉 同行、同列 的其他0元素，以此类推。
   5. 若矩阵中加圈0元素的个数等于 m（矩阵的阶数），则该指派方案为最优方案。若矩阵中加圈0元素的个数小于 m，则进行下面第三步
3. 作 最小 能覆盖 所有0元素 的直线集合，由此确定该系数矩阵中能找到最多的 独立元素数。依据原理：该直线集合条数 = 已划去的圈数⭕
   1. 对没有⭕的行打✔
   2. 对已✔行上的所有$\times $元素所在的列打✔
   3. 再对已✔的列上有⭕的行打✔
   4. 重复2、3操作，直至得不到新的打✔行、列为止
   5. 对所有 没有 ✔的行画一条横线，对所有 有 ✔的列画纵线，由此得到覆盖所有0元素的最小直线集合
4. 进行调整（对矩阵进行变换，其目的是增加0元素）
   • 对直线 未覆盖区 的所有元素减去它们中的 最小数；覆盖区的交叉元素 加上刚才的最小数，其他元素不变，转向步骤 2 继续操作