对偶理论

作者：@硫没有正七价
本文为作者原创，转载请注明出处：https://www.cnblogs.com/wendaidai/p/16417609.html

---

对偶理论

对偶问题的提出

• 从数学角度，对偶问题可以被理解为寻找原问题目标函数上届或下届的问题

• 一个例子引出对偶问题：

  企业A拥有m种资源（有m个约束条件），可以消耗资源生产出n种商品（有n个变量），目标是最大化收入；那么其对偶问题就是，企业B想要购进这些资源，需要确定m种资源的报价（有m个变量），目标是最小化成本，但企业A只有在卖资源的收益不低于卖产品的时候才会同意卖资源（n个约束）。

对偶问题的用途

• 原问题约束多、变量少时，求解对偶问题能够降低计算时间
  使用单纯形法时，如果原问题约束多变量少，转换成对偶问题，就是约束少变量多。约束的减少能够有效降低单纯形法的计算时间
• 帮助证明原问题无解
  类似”证明无罪比证明有罪更难“，要证明原问题有解，只需要找出一个满足约束的点，但是想证明原问题无解，总不能遍历所有的点来证明。对偶问题的出现为证明原问题无解提供了新思路。
• 便于进行敏感度分析
  除了得到最优解，我们可能还会关注”如果某些一直条件发生变化，对最优解的影响程度如何“，这就是敏感度分析
  • 增加敏感度分析的直观程度（对偶问题的最优解就是原问题约束的影子价格）
  • 在改变某些条件导致原问题无可行解时，可以借助仍然有可行解的对偶问题来分析。

---

对偶问题的一般形式

若原问题为$LP_1$

$$max\ z\ =\ CX \\ s.t.\begin{cases} AX\ \le\ b \\ X\ \ge \ b \end{cases}$$

则其对偶问题定义为 $LP_2$

$$min\ w\ =\ Y^{T}b \\ s.t.\begin{cases} A^{T}Y\ \ge \ C^{T} \\ Y\ \ge \ 0 \end{cases}$$

若原问题并非$LP_1$形式，则我们可以首先将其转化为$LP_1$形式，然后按照前面定义即可计算出其对偶问题。

$$\sum_{i=1}^na_{ij}x_j\ =\ b_i \implies\ \begin{cases} \displaystyle \sum_{i=1}^na_{ij}x_j\ \le\ b_i \\ \displaystyle \sum_{i=1}^n-a_{ij}x_j\ \le\ -b_i \end{cases} \\ \displaystyle \sum_{i=1}^na_{ij}x_j\ \ge \ b_i\ \implies\ \displaystyle \sum_{i=1}^n-a_{ij}x_j\ \le \ -b_i$$

可以采用如下方法进行转换：

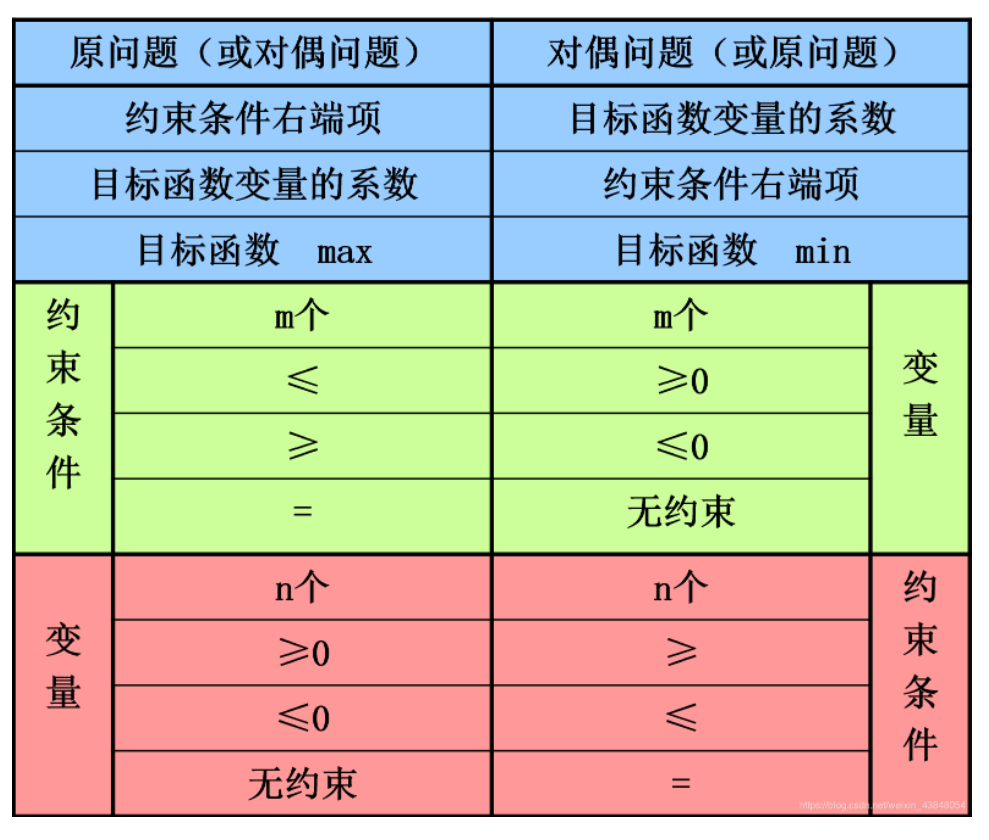
对照可以看出：

• 原问题中求解目标函数极大化，对偶问题求解目标函数极小化
• 原问题中约束条件个数等于对偶问题中变量的个数，原问题中变量个数等于对偶问题中约束条件个数
• 原问题中约束条件符号为 $\le$，对偶问题中约束条件符号为 $\ge$
• 原问题目标函数的系数是其对偶问题约束条件的右端项，而原问题约束条件的右端项是其对偶问题目标函数的系数

举个例子：

原问题：

$$\min_{}\ z\ =\ 7x_1\ +\ 4x_2\ -\ 3x_3 \\ s.t. \begin{cases} -4x_1+2x_2-6x_3\ \le \ 24 \\ -3x_1-6x_2-4x_3\ \ge \ 15 \\ \qquad\quad\ \ 5x_2+x_3\ =\ 30\\ x_1\le 0,x_2\text{无约束}，x_3\ge 0 \end{cases}$$

首先把 $C$ 和b互换，A转置

$$\max_{}\ w\ =\ 24 \quad 15 \quad 30 \\ s.t. \begin{cases} -4 \quad -3 \quad 0 \quad\ 7\\ 2 \quad -6 \quad 5 \quad\ 4\\ -6 \quad -4 \quad 1 \quad\ -3\\ \end{cases}$$

最小化转最大化，所以约束条件和原问题变量的符号相反（也就是表格中从右往左），变量和原问题约束条件符号相同：

$$\max_{}\ w\ =\ 24y_1\ +\ 15y_2 \ +\ 30y_3 \\ s.t. \begin{cases} -4y_1 -3y_2 \quad \quad\ \ \ge7\\ 2y_1 -6y_2+5y_3\ \ \ = 4\\ -6y_1 -4y_2 +1y_3\le -3\\ \end{cases}$$

---

对偶问题的基本性质

1. 弱对偶性：如果$X$是原问题的可行解，$Y$是对偶问题的可行解，则$CX\ \le\ Y^{T}b$
   证明：$Y^{T}\ge Y^{T}AX\ =\ (Y^{T}AX)^{T}\ =\ X^{T}A^{T}Y\ge X^{T}C^{T}\ =\ CX$
   推论：
   • 最优性：如果$X$是原问题的可行解，$Y$是对偶问题的可行解, 且$CX\ =\ Y^{T}b$，则$X$和$Y$分别为原问题和对偶问题的最优解
   • 无界性：如果原问题（对偶问题）具有无界解，则其对偶问题（原问题）无可行解
2. 强对偶性：如果原问题有最优解，则其对偶问题也一定具有最优解，
   且$\max_{}\ z\ =\ \min_{}\ w$
   证明：设B为原问题标准形式的可行解基，且其基解为最优解，则由最优性条件应有检验数全部小于等于零：
   $-C_{B}B^{-1}\le 0,\theta=C-C_{B}B^{-1}A\le 0$
   从而可得：
   $A^{T}B^{-T}C^{T}_B\ge C^{T},B^{-T}C^{T}_B\ge 0$
   所以$B^{-T}C^{T}_B$是对偶问题的一个可行解，且
   $(B^{-T}C^{T}_B)^{T}b=C_BB^{-1}b=\max_{}\ z$
   由最优性可知，$B^{-T}C^{T}_B$为对偶问题的最优解，且$\max_{}\ z\ =\ \min_{}\ w$
3. 互补松弛性：在线性规划问题的最优解中，如果某一约束条件的对偶变量值非零，则该约束条件严格取等，反之，如果约束条件取不等式，则对应的对偶变量一定为0，可以表示为$Y^{T}(b-AX)\ =\ 0$
   证明：由强弱偶性可知$CX\ =\ Y^{T}b$，
   又$\because\ CX=X^{T}C^{T}\le X^{T}A^{T}Y=Y^{T}AX\le Y^{T}b$
   $\therefore Y^{T}AX=Y^{T}b \implies Y^{T}(b-AX)\ =\ 0$
4. 基解互补性：原问题及其对偶问题之间存在一对互补的基解，其中原问题的松弛变量对应对偶问题的变量对偶问题的剩余变量对应原问题的变量.这些互相对应的变量如果在一个问题的解中是基变量则在另一个问题的解中是非基变量；将这对互补的集解分别带入原问题和对偶问题的目标函数中有$z\ =\ w$

---

影子价格

考察如下对偶问题

$$max\ z\ =\ CX \quad \quad min\ w\ =\ Y^{T}b \\\\ s.t.\begin{cases} AX\ \le\ b \\ X\ \ge \ b \end{cases} \quad \quad s.t.\begin{cases} A^{T}Y\ \ge \ C^{T} \\ Y\ \ge \ 0 \end{cases}$$

定义：若P的某个约束条件的右端项常数$b_i$(第i种资源的拥有量）增加一个单位时，所引起目标函数最优值$z^{*}$的改变量称为第i种资源的影子价格，其值等于对偶问题中对偶变量$y_i$.

假设$X^{*}$和$Y^{*}$分别为原问题和对偶问题的最优解，由对偶问题的基本性质有

$$z^{*}=\sum c_j x_j^{*}=\sum b_j y_j^{*}$$

$\because$ 某个 $\Delta b_i=1$ ，所以最优解的变化$\Delta z^{*}=y_i^{*}$
也就是对偶变量$y_i$就是第i个产品的影子价格$\displaystyle \frac{\partial z^{*}}{\partial b_i}=y^{*}_i$

影子价格是在资源最优利用条件下对单位资源的估价，这种估价不是资源实际的市场价格。影子价格是一种机会成本。

根据影子价格得出的结论

假设某种资源的单位市场价是$m_i$，则

• 当$j_i^{*} > m_i$时，企业购进这种资源后增加的利润多于资源收购价，单位纯利为$j_i^{*} - m_i$，企业有利可图
• 相反，当$j_i^{*} < m_i$时，则企业会选择有偿转让这种资源，可获单位纯利$j_i^{*} - m_i$，否则企业无利可图，甚至亏损

根据互补松弛性：$Y^{T}(b-AX)\ =\ 0$，可以进一步得出结论：

• 生产过程中如果某种资源未得到充分利用时（资源约束不严格取等），该种资源的影子价格为0（对偶问题的最优解对应变量为0）
• 若当资源的影子价格不为0时，表明该种资源在生产中已耗费完（资源约束严格取等）

影子价格对单纯形表计算的解释
在单纯形表中的检验数为$\sigma_j=c_j-C_BB^{-1}P_j=c_j-\displaystyle \sum_{i=1}^m a_{ij}y_i$，其中$c_j$代表第j种产品的产值，$\displaystyle \sum_{i=1}^m a_{ij}y_i$代表生产一个单位该种产品所消耗的各项资源的影子价格的总和，即产品的机会成本
则检验数$\sigma_j$的经济意义如下

• 当$\sigma_j>0$时，即产值大于记会成本时，表明生产该项产品更有利，可在计划中安排
• 反之，当$\sigma_j<0$时，表明用这些资源生产别的产品更有利，不应用于生产该产品

---

对偶单纯形法

对偶单纯形法是求解线性规划的另一个基本方法。它是根据对偶原理和单纯形法原理而设计出来的，因此称为对偶单纯形法。对偶单纯性法提高了对求解线性规划问题的效率，它通常具有以下优点：

• 初始基解可以是非可行解, 当检验数都为负值时, 就可以进行基的变换, 不需加入人工变量, 从而简化计算；
• 对于变量多于约束条件的线性规划问题,用对偶单纯形法可以减少计算量,在灵敏度分析及求解整数规划的割平面法中,有时适宜用对偶规划单纯形法。

而在对偶单纯形方法中，我们要求：所有检验数$\sigma<0$，但是b无要求。这时我们希望通过转化可行解使得$b=(b_1,b_2,\cdots,b_m)^{T}$更接近$\ge 0$，同时保持$\sigma\le 0$，直到$b\ge 0$，找到最优解。

对偶单纯形法计算步骤：

1. 确定换出基变量
   对于小于零的$b_i$，令$b_r=\min_{}(b_i)$，所对应的变量$x_r$为换出基变量。
2. 确定换入基变量
   1. 为使迭代后的表中第r行基变量为正值，
      因而只有对应$a_{rj}<0(j=m+1,\cdots,n)$(系数均为负数)的非基变量才可以考虑
   2. 为使迭代后表中对偶问题的解仍为可行解，令
   $$\displaystyle \theta = \min_{j}\left\{ \frac{\sigma_j}{a_{rj}} \mid a_{rj}<0 \right\} = \frac{\sigma_s}{a_{rs}}$$
   称$a_{rs}$为主元素，$x_s$为换入基变量
3. 用换入基变量替换换出基变量，得到一个新的基
   进行初等行变换后，检查所有$b_i$是否$\ge 0$
4. 重复上述三个步骤，直至$b\ge 0$

单纯行表如下：

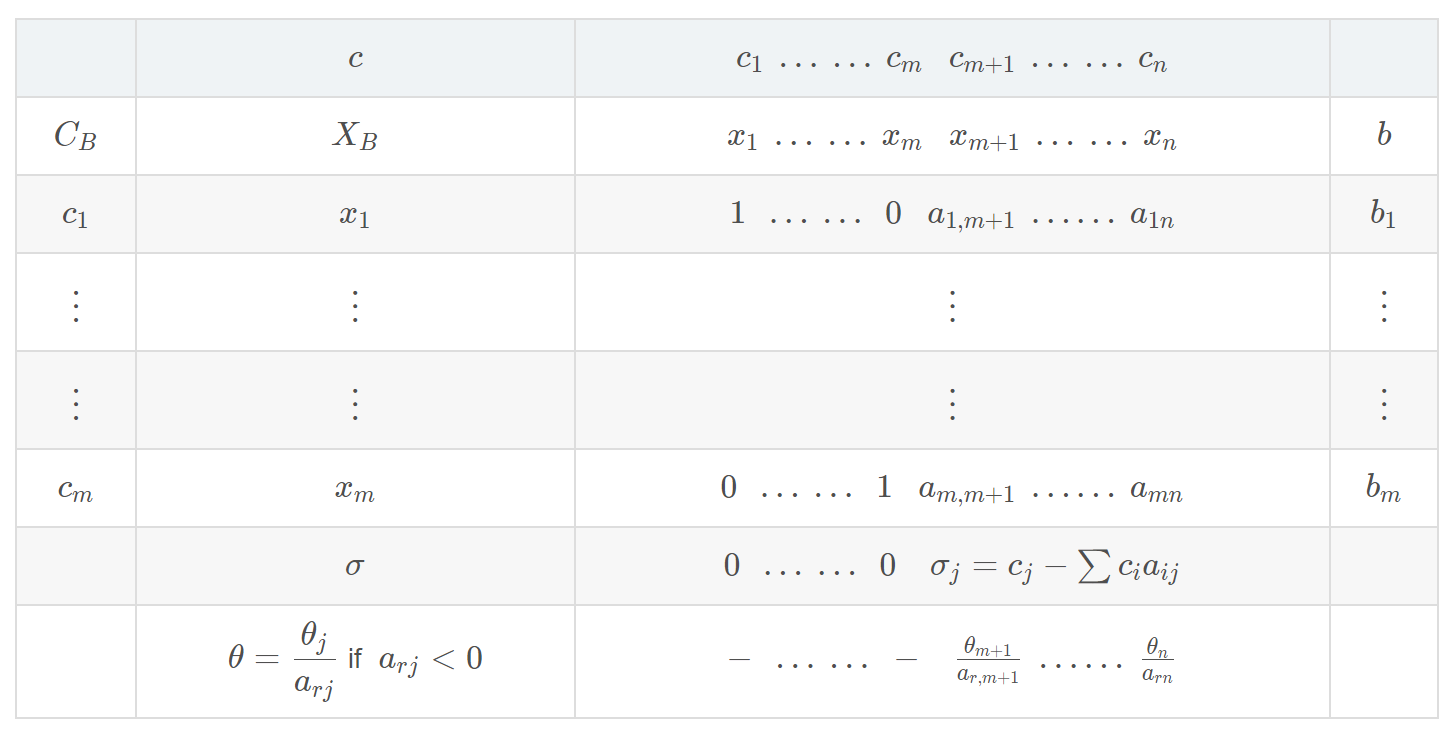
单纯形法与对偶单纯形法的比较

	单纯形法	对偶单纯形法
原理	保证原问题是可行解的情况下 向对偶问题可行的方向迭代	保证对偶问题是可行解的情况下 向原问题可行的方向迭代
限制条件	单纯形表的 b ≥ 0（找到基可行解）	检验数字 σ ≤ 0
最优解判断	看非基变量的检验数是否都 ≤ 0	看对偶单纯形表的 b 是否都 ≥ 0
变量替换	先确定入基变量，最小换最大	先确定换出变量，最小换最大

---

灵敏度分析

在前面的线性规划问题中，我们都是假定问题中的$A,b,C$是已知的。但是实际上这些参数往往是一些估计和预测的数字，如市场条件发生变化，C的值就会变化，A会随着工艺技术条件的改变而改变，而b则是根据资源投入后能产生多大经济效果来决定的一种决策选择。

因而一个自然的问题就是当这些参数中的一个或者几个发生变化时，问题的最优解会有什么变化，或者这些参数在一个多大的范围内变化时，问题的最优解或者最优基不变，这就是灵敏度分析所要解决的问题。

在使用单纯形法解决线性规划问题时，我们需要先通过初等行变换基变量对应的子矩阵化为单位矩阵，因此存在一个方阵D使得$\displaystyle D(A\ b) = (A^{'}\ b^{'})$，易得$D\ =\ B^{-1}$，一般来讲，我们考虑如下几种问题的变化：

1. 当某个$c_j$变化时，$A^{'}\ b^{'}$无变化，非基变量的检验数$\Delta\sigma_j=-a_{ij}\Delta c_j$，要让最优解不发生变化，我们要求所有$\sigma^{*}_j=\sigma_j+\Delta\sigma_j\le 0$
2. 当某个$b_j$变化时，$\Delta b^{'}=B^{-1}\Delta b$，要让最优解不发生变化，我们要求
   $b^{*}=b+B^{-1}\Delta b\ge 0$
3. 增加某个变量$x_j$，对应的系数列向量为$P_j$，则单纯形表中需要新添加一列
   $P^{'}_j=B^{-1}P_j$，然后计算相应的检验数，继续用单纯形法计算最优解
4. 增加一个约束条件，新产生一个剩余变量或者松弛变量，或者用前面学过的方法添加人工变量，将新变量加入基变量，重整单纯性表，根据 b 和 $\sigma$ 的情况选择方法求出最优解。