K-means分箱

 

一、“分箱”定义

各行各业的打工人，经常会面对一种令人尴尬的质疑：为什么你把15-25归为一类，10-20不行吗？13-23不行吗？

 

以及地产干饭人经常会被问到的：120-140㎡是主力，那119㎡行不行，118㎡呢？这个时候，通常大部分人会说那样也行。

 

可是那样真的行吗？吾不以为然也。而且，不但那样不行，这样也不是很行。提出问题，自然也要解决问题，下面就让我们一起来看看，怎样才算是真的行。

 

当我们在把一组连续的数据，进行分段研究的时候，这就是“分箱”。

 

意思是把一些初始元素，放到不同的“箱子”里去，用于增强数据的粒度，便于研究。比如把月薪水*分为：5000以下、5000-8000、8000-10000、10000-20000、20000以上。有时候分箱也可以进行调整和改变，比如薪酬也可以直接分成“8000以上”和“8000以下”。

 

同样，性别既可以分为4个箱：“男”、“女”、“无性别”、“双性别”；也可以分为2个箱：“性别明确”和“性别不明确”。

 

那么问题就来了，到底分成几个箱，以及按照怎样的标准来划分才更合适呢？

 

首先，最简单的是等距分箱、等频分箱以及自定义分箱。

 

所谓等距分箱，就是隔着同样的距离把整体切分。比如将薪酬按照1000-2000、2000-3000、3000-4000这样每隔1000分一段。亦或者将房地产产品面积按照每隔10*米划分为80-90、90-100、100-110、110-120。

 

而等频分箱，就是把整体每隔n个元素放在一起作为一个箱，比如一共有1000个样本，我们按照从小到大的顺序排序后，把前250个作为第一类。

 

自定义分箱就是通过经验和判断进行划分，或者说就是拍脑袋的。就比如我们把月薪分为了5000以下、5000-8000、8000-10000、10000-20000。

 

对于有些情况，自定义分箱是个不错的选择，有时候自定义分箱，也可以在其他分箱的基础上，来补充一些数据上无法体现的东西。

 

比如我们的模型里有“年龄”这一维度的数据，而研究目标是青少年的犯罪率，那么就应该适当地把年龄分为14岁以下、14-16岁、16岁以上（因为刑法规定14岁以下完全不承担任何刑事责任！）。

 

当然也有用各种各样有监督的无监督的手段来分箱的，都可以进行尝试。但今天我们要说的是一个纯粹根据数据分布规律进行分箱的策略——K-means分箱。

 

 

二、K-means分箱算法

K-means即K均值聚类算法，如果用过聚类的朋友们肯定就对它很熟悉了，这是最简单有效的聚类方式之一。

 

首先需要指定一个大于1的正整数K，然后随机选取K个元素作为整体的聚类中心，随后计算每个对象与各聚类中心的几何距离，用于把每个对象分配给不同的聚类中心，再计算形成的每个簇的新几何中心作为新的聚类中心，重复这一过程直到每个聚类中心不再变化。

 

K-means算法最大的优点，是它可以对于任意大于1的正整数K，根据数据的几何分布，来把数据划分成几类，显然K越大，分类效果越好，但为了避免过拟合的情况出现，我们也可以人为规定一个K，或者是K的上限，也可以通过一个判断来选择最优的K是多少。

 

对于K-means算法，在一维数组中也是可以用的，当然在多维度空间中也是可行的（就是统计学常用的K-means聚类，顺便说一下这也是通常K-means聚类不可以用于逻辑变量的原因，不要再乱用了同学们）。

 

大部分数据分析软件都有K-means现成的包，笔者认为相比于python和R， Matlab在数据处理上总是更胜一筹，最后也会给大家分享案例实现的代码。

 

K-means的核心在于，通过计算机去寻找数据的聚集点，从而在分箱的同时，避免了过多的信息丢失。

 

 

三、案例实现

假设我们现在有一些房地产项目的成交明细数据，其中有一列为面积，我们在研究中通常需要对分面积段进行研究，那么我们就需要把面积离散化，也就是进行分箱处理。

 

就以60-100*内的产品分4个箱为例进行研究。（数据样例）

 

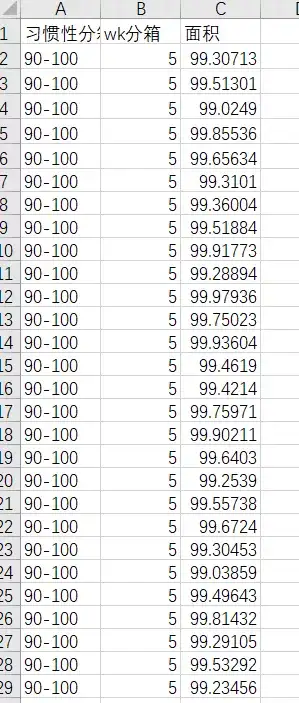
传统房地产人会通过经验来定一些整数分段，比如60-80*、80-100*、100-120*这样，当然这也不是不行，我们就以10*米来分段，60-100之间被分成了4段。

 

经验性分箱	方差	占比
[60-70）	0.19	7%
[70-80）	17.26	11%
[80-90）	17.81	34%
[90-100）	14.89	47%
总方差	15.07

 

可以看到此时总方差来到了15.07。

 

那么我们用W-K分箱（加权kmeans，在kmeans分箱的基础上附上套数作为权重），就可以得到结果如下

 

W-K分箱	方差	占比
[69-72）	0.67	12%
[79-82）	0.67	22%
[89-92）	0.81	45%
[98-100）	0.23	21%
总方差	0.65

此时总方差仅有0.65，分箱效果碾压。

 

最后结果也就是89-91*是一个主力面积段，如果数据的分布改变了，分箱的间断点也会随之改变。

 

但经验法却总是会指引你去做90-99的产品，也就是有接*10*米的误差了，当然有的人会说，我经验丰富，总是能拍的很准，那也没问题，只是说如果总想用经验，其实很难每次都能获得正确的结论，就像玩俄罗斯轮盘，看起来这是个很简单的游戏，而且听说很少有人在自己的一生中会输第二次。

 

更何况算法分箱在无形之中降低了房地产的经验门槛，而且也更加合理。