卡尔曼滤波+单目标追踪+python-opencv
向面试官一句话解释卡尔曼滤波：
- 用上一次的最优状态估计和最优估计误差去计算这一次的先验状态估计和先验误差估计；
- 用1得到的本次先验误差估计和测量噪声，得到卡尔曼增益；
- 用1，2步骤得到所有先验误差估计和测量噪声，得到本次的最优估计。
一句话解释：对模型的预测值和实际的观测值进行加权，迭代计算出未来的状态。
对于上面三句话的一些解释：
- 先验：根据以往的结果去推导
- 后验：得到当前结果之后再去修正
- 卡尔曼增益作用：将“粗略估计”变成“最准确的估计”
卡尔曼滤波解决的根本问题：如何让噪声的干扰最小（噪声：可以理解为 实际值-预测值 最小）
卡尔曼滤波的本质：参数化的贝叶斯模型
算法核心思想：根据当前的仪器“测量值”和上一刻的“预测值”和“误差”，计算得到当前的最优量，再预测下一刻的量。
为什么称卡尔曼滤波：首先，是卡尔曼本人提出来的；其次，输出变量都是输入变量的线性组合，所以可以看做是一种滤波算法。
卡尔曼滤波器可以从最小均方误差的角度推导出，也可以从贝叶斯推断的角度来推导。
下面从最小均方误差的角度推导卡尔曼滤波。
基础背景知识
卡尔曼的核心：预测＋反馈
观测数据：代表传感器采集的实际数据，可能存在或多或少的误差
最优估计：算法计算出来接近于真实值的估计
均方误差：误差（每个估计值与真实值的差）的平方，再求和，再求平均。多样本时，均方误差等于每个样本的误差平方乘以该样本出现的概率，再求和。
方差：描述随机变量的离散程度，具体来说是变量值离期望值的距离。
最小均方误差估计：估计参数，使得估计出来的模型和真实值之间的误差平方期望最小。
两个变量之间的协方差：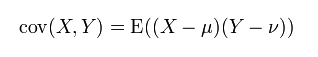
x==y，就是方差。在协方差矩阵中，对角线元素即为方差。x, y都大于期望，协方差为正直；相应自行分析。
卡尔曼滤波核心公式及解释
V(k)为测量噪声
Z(K)为K时刻的测量值
python-opencv 中的kalman滤波模块
应用重点说明：
A: 转移矩阵
B: 控制矩阵
H：测量矩阵
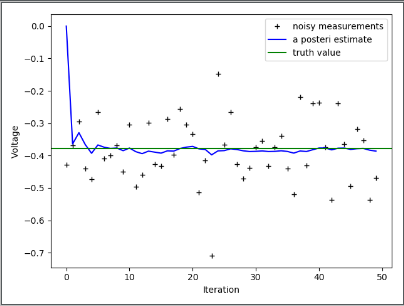
一维中的卡尔曼滤波实现（注重原理的理解）
import numpy as np
import matplotlib.pyplot as plt
#这里是假设A=1，H=1, B=0的情况
# 故动态模型 X(k) = X(k-1) + 噪声
# Z(K) = X(k)
# 动态模型是一个常量
# intial parameters
n_iter = 50
sz = (n_iter,) # size of array
x = -0.37727 # truth value (typo in example at top of p. 13 calls this z)
z = np.random.normal(x,0.1,size=sz) # observations (normal about x, sigma=0.1)
Q = 1e-5 # process variance
# allocate space for arrays
xhat=np.zeros(sz) # a posteri estimate of x
P=np.zeros(sz) # a posteri error estimate
xhatminus=np.zeros(sz) # a priori estimate of x
Pminus=np.zeros(sz) # a priori error estimate
K=np.zeros(sz) # gain or blending factor
R = 0.1**2 # estimate of measurement variance, change to see effect
# intial guesses
xhat[0] = 0.0
P[0] = 1.0
for k in range(1,n_iter):
# time update
xhatminus[k] = xhat[k-1] #X(k|k-1) = AX(k-1|k-1) + BU(k) + W(k),A=1,BU(k) = 0
Pminus[k] = P[k-1]+Q #P(k|k-1) = AP(k-1|k-1)A' + Q(k) ,A=1
# measurement update
K[k] = Pminus[k]/( Pminus[k]+R ) #Kg(k)=P(k|k-1)H'/[HP(k|k-1)H' + R],H=1
xhat[k] = xhatminus[k]+K[k]*(z[k]-xhatminus[k]) #X(k|k) = X(k|k-1) + Kg(k)[Z(k) - HX(k|k-1)], H=1
P[k] = (1-K[k])*Pminus[k] #P(k|k) = (1 - Kg(k)H)P(k|k-1), H=1
plt.figure()
plt.plot(z, 'k+', label='noisy measurements') # 测量值
plt.plot(xhat, 'b-', label='a posteri estimate') # 过滤后的值
plt.axhline(x, color='g', label='truth value') # 系统值
plt.legend()
plt.xlabel('Iteration')
plt.ylabel('Voltage')
plt.show()
