动态规划-最长公共子序列

---

1、最长公共子序列问题是一个组合优化问题，序列X=<x1,x2,x3,....,xm>,序列Y=<y1,y2,y3,...,yn>的公共子序列有很多
，要找出最长的那个解。由于X的子序列有2的m次幂这么多，Y的子序列也有2的n次幂这么多，所以传统解法：先求出X和Y的所有
子序列，再去找最长的公共子序列，复杂度很高。

---

2、检验能否利用：动态规划法（记表备查）
需要满足两个条件：

• 最优子结构
• 子问题重叠

最优子结构：最优解的子解也是某一个子问题的最优解

设Z=<z1,z2,z3,...,zk>是X和Y的最长公共子序列

则有：

（1）当xm==yn时，zk=xm=yn,且Z_k-1是X_m-1和Y_{n-1    的最长公共子序列}

（2）当xm!=yn时，zk!=xm,则Z是X_m-1和Y    _{的最长公共子序列}

(3) 当xm!=yn时，zk!=yn,则Z是X和Y_{n-1    的最长公共子序列}

设C[i][j]为长度为i的序列X=<x1,x2,x3,...,xi>和长度为j的序列Y = <y1,y2,...,yj>的最长公共子序列的长度，则有：

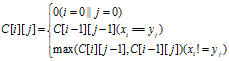
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <limits.h>

int* lcsLength(char* X,char* Y,int m,int n)
{
    int i = 0,j = 0;
    int* C = (int*)malloc(sizeof(int)*(m+1)*(n+1));
    memset(C,0,sizeof(int)*(m+1)*(n+1));
    for(i=0;i<=m;i++)
    {
        for(j=0;j<=n;j++)
        {
            if(i==0 || j==0)
                C[i*(n+1)+j] = 0;
            else if(X[i-1] == Y[j-1])
                C[i*(n+1)+j] = C[(i-1)*(n+1)+j-1] + 1;
            else
                C[i*(n+1)+j] = (C[i*(n+1)+j-1] - C[(i-1)*(n+1)+j]>0)?C[i*(n+1)+j-1]:C[(i-1)*(n+1)+j];

        }
    }
    
    return C;
    


}

//打印最长公共子序列
void printLcs(int* C,int n,char* X,char* Y,int i,int j)
{
    if(i==0||j==0)
        return;
    if(X[i-1] == X[j-1])
    {
        printLcs(C,n,X,Y,i-1,j-1);
        printf("%c ",X[i-1]);
    }
    else if(C[(i-1)*(n+1)+j] >= C[i*(n+1)+j-1])
    {
        printLcs(C,n,X,Y,i-1,j);
    }
    else
        printLcs(C,n,X,Y,i,j-1);

}

 

int main()
{
    char X[] = {'A','B','C','B','D','A','B'};
    char Y[] = {'B','D','C','A','B','A'};
    int m = sizeof(X)/sizeof(char);
    int n = sizeof(Y)/sizeof(char);
    int* C = lcsLength(X,Y,m,n);
    printf("%d\n",C[m*(n+1)+n]);
    free(C);

    return 0;
}

---