特征值、特征向量与PCA算法
一、复习几个矩阵的基本知识
1. 向量
1)既有大小又有方向的量成为向量,物理学中也被称为矢量,向量的坐标表示a=(2,3),意为a=2*i + 3*j,其中i,j分别是x,y轴的单位向量。
2)向量的点乘:a · b
公式:a · b = b · a = |a| * |b| * cosθ = x1 * x2 + y1 * y2
点乘又叫向量的内积、数量积,是一个向量a和它在另一个向量b上的投影的长度的乘积,结果是一个标量;
如果两个向量的点乘是零, 那么这两个向量正交。
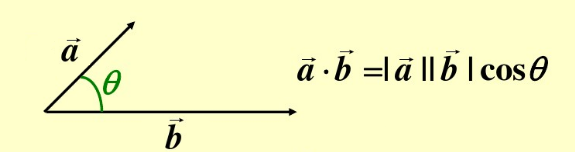
2)向量的叉乘:a X b

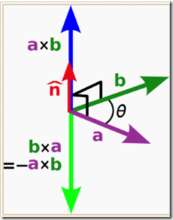
3)三维向量的叉乘公式,摘自向量叉乘

2. 矩阵的行列式

3. 线性方程组求解
1)齐次和非齐次线性方程组

2)使用行列式求解线性方程组

4. 矩阵的特征值和特征向量
1)定义


2)示例


二、PCA算法
PCA是一种较为常用的降维技术,PCA的思想是将n维特征映射到k维上,这k维是全新的正交特征。这k维特征称为主元,是重新构造出来的k维特征。在PCA中,数据从原来的坐标系转换到新的坐标系下,新的坐标系的选择与数据本身是密切相关的。其中,第一个新坐标轴选择的是原始数据中方差最大的方向,第二个新坐标轴选取的是与第一个坐标轴正交且具有最大方差的方向,依次类推,我们可以取到这样的k个坐标轴。
1. PCA的操作流程大致如下:
- 去平均值,即每一位特征减去各自的平均值
- 计算协方差矩阵
- 计算协方差矩阵的特征值与特征向量
- 对特征值从大到小排序
- 保留最大的k个特征向量
- 将数据转换到k个特征向量构建的新空间中
摘自: https://blog.csdn.net/google19890102/article/details/27969459
2. 经过数学上的推导的,我们就可以知道,特征值对应的特征向量就是理想中想取得正确的坐标轴,而特征值就等于数据在旋转之后的坐标上对应维度上的方差,所以可以根据特征值判断直线还是平面。

摘自: https://blog.csdn.net/fuming2021118535/article/details/51339881
3. 那么问题来了,为什么样本协方差矩阵的特征向量就是样本分散度最大的方向,相应的特征值就是在该方向的分散度——方差?
讨论: https://www.zhihu.com/question/36348219



 浙公网安备 33010602011771号
浙公网安备 33010602011771号