Kdtree原理以及 vs Octree
1. Kdtree原理
Kdtree是一种划分k维数据空间的数据结构,本质也是一颗二叉树,只不过每个节点的数据都是k维,当k=1时,就是图1所示的普通二叉树。
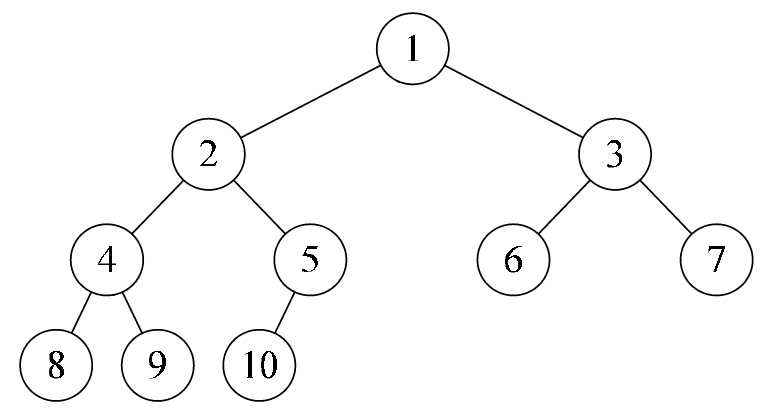
图1
1)Kdtree的建立
建立Kdtree实际上是一个不断划分的过程,首先选择最sparse的维度(一般通过计算数据在各个维度的方差,选择方差大的作为本次分割维度),然后找到该维度上的中间点,垂直该维度做第一次划分。此时k维超平面被一分为二,在两个子平面中再找最sparse的维度,以此类推直到最后一个点也被划分,那么就形了一个不断二分的树。
二维Kdtree的建立过程如图2所示,首先分别计算x,y方向上数据的方差,得知x方向上的方差最大,所以split域值首先x轴方向;然后根据x轴方向的值2,5,9,4,8,7排序选出中值为7,所以Node-data = (7,2)。这样,该节点的分割超平面就是通过(7,2)并垂直于split = 0(x轴)的直线x = 7,后面以此类推。
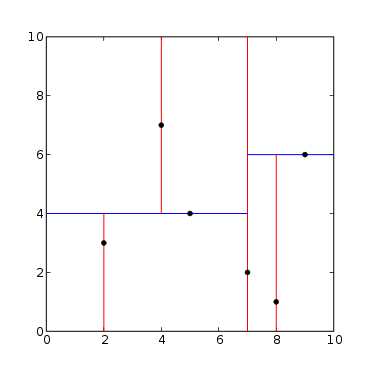 图2
图2
三维Kdtree的建立过程:The first split (the red vertical plane) cuts the root cell (white) into two subcells, each of which is then split (by the green horizontal planes) into two subcells. Finally, those four cells are split (by the four blue vertical planes) into two subcells. Since there is no more splitting, the final eight are called leaf cells.
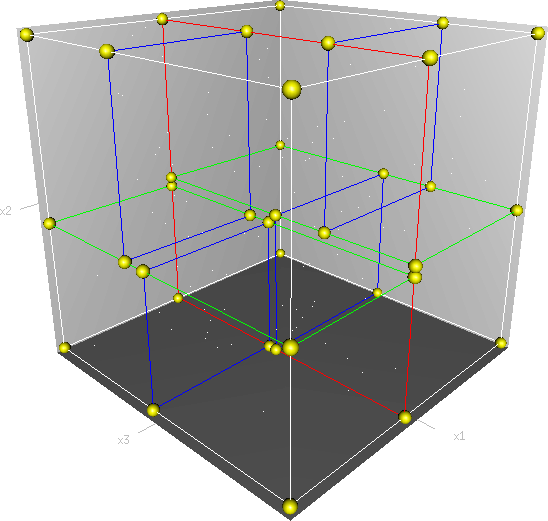
图3
2)Kdtree的搜索
搜索一般有:1. 搜索距离search point 一定radius范围内的所有点;2. 搜索距离search point最近的k个点。
星号表示要查询的点(2.1,3.1),通过二叉搜索,顺着搜索路径很快就能找到最邻近的近似点,也就是叶子节点(2,3)。而找到的叶子节点并不一定就是最邻近的,最邻近肯定距离查询点更近,应该位于以查询点为圆心且通过叶子节点的圆域内。为了找到真正的最近邻,还需要进行'回溯'操作:算法沿搜索路径反向查找是否有距离查询点更近的数据点。 此例中先从(7,2)点开始进行二叉查找,然后到达(5,4),最后到达(2,3),此时搜索路径中的节点为<(7,2),(5,4),(2,3)>,首先以(2,3)作为当前最近邻点,计算其到查询点(2.1,3.1)的距离为0.1414,然后回溯到其父节点(5,4),并判断在该父节点的其他子节点空间中是否有距离查询点更近的数据点。以(2.1,3.1)为圆心,以0.1414为半径画圆,如图4所示。发现该圆并不和超平面y = 4交割,因此不用进入(5,4)节点右子空间中去搜索。再回溯到(7,2),以(2.1,3.1)为圆心,以0.1414为半径的圆更不会与x = 7超平面交割,因此不用进入(7,2)右子空间进行查找。至此,搜索路径中的节点已经全部回溯完,结束整个搜索,返回最近邻点(2,3),最近距离为0.1414。
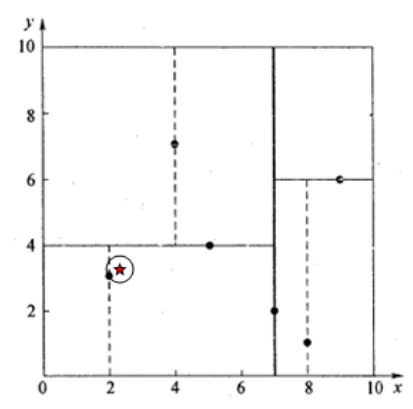 图4
图4
一个复杂点了例子如查找点为(2,4.5),同样先进行二叉查找,先从(7,2)查找到(5,4)节点,在进行查找时是由y = 4为分割超平面的,由于查找点为y值为4.5,因此进入右子空间查找到(4,7),形成搜索路径<(7,2),(5,4),(4,7)>,取(4,7)为当前最近邻点,计算其与目标查找点的距离为3.202。然后回溯到(5,4),计算其与查找点之间的距离为3.041。以(2,4.5)为圆心,以3.041为半径作圆,如图5所示。可见该圆和y = 4超平面交割,所以需要进入(5,4)左子空间进行查找。此时需将(2,3)节点加入搜索路径中得<(7,2),(2,3)>。回溯至(2,3)叶子节点,(2,3)距离(2,4.5)比(5,4)要近,所以最近邻点更新为(2,3),最近距离更新为1.5。回溯至(7,2),以(2,4.5)为圆心1.5为半径作圆,并不和x = 7分割超平面交割,如图6所示。至此,搜索路径回溯完,返回最近邻点(2,3),最近距离1.5。
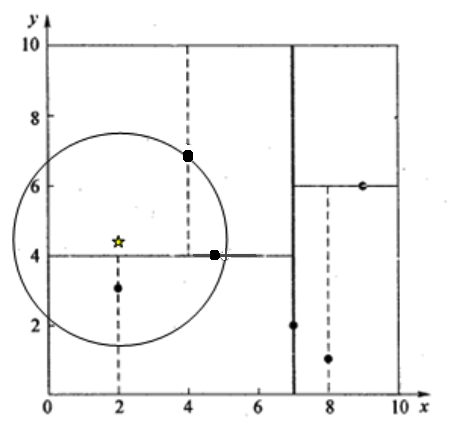
图5
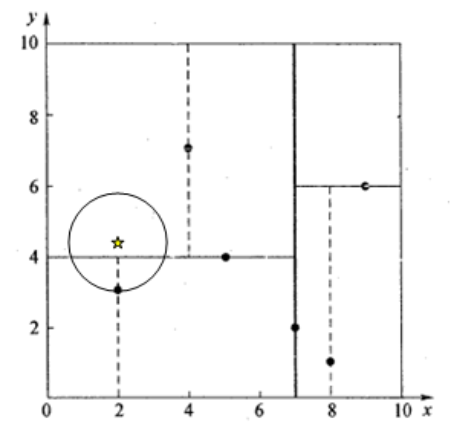
图6
2. Kdtree vs Octree
显然,对于不同点云应该采取不同的搜索策略,如果点云是疏散的,分布很广泛,且每什么规律(如lidar测得的点云或双目视觉捕捉的点云)Kdtree能更好的划分,而Octree则很难决定最小立方体应该是多少,太大则一个立方体里可能有很多点云,太小则可能立方体之间连不起来。如果点云分布非常规整,是某个特定物体的点云模型,则应该使用Octree,因为很容易求解凸包并且点与点之间相对距离无需再次比对父节点和子节点,更加明晰,典型的例子是斯坦福的兔子。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号