有向图的强连通分量

简单介绍：

　　连通分量：对于分量中任意两点u、v，必然可以从u走到v且从v走到u。

　　强连通分量：极大连通分量

核心思路：

　　将有向图通过缩点（把所有连通分量缩成一个点）变成拓扑图（DAG）

 

 

 

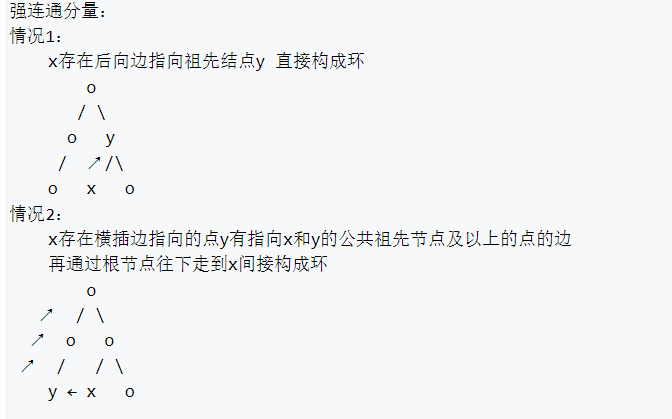
新概念：

　　1.时间戳（按dfs回溯顺序标记）

　　2.dfn[u]表示dfs遍历到u的时间，low[u]表示从u开始走所能遍历到的最小时间戳

　　    u是其所在强连通分量的最高点 <==> dfs[u]==low[u]

　　3.缩点

　　　　for(i=1;i<=n;i++)

　　　　　for i的所有邻点j

　　　　　　if i和j不在同一个scc中，加一条新边id[i] -> id[j]

　　4.缩完点后就变成了有向无环图DAG，就可以做拓扑排序了（此时连通分量编号id[ ]递减的顺序（for i=scc_cnt;i>=1;i--)就是拓扑序。

　　　　因为++scc_cnt是在dfs完节点i的子节点j后才判断low[u]==dfn[u]后才加的，　那么子节点j如果是强连通分量 scc_id[j]一定小于scc_id[i]。

 

题型一：求有向图中出度为0的强连通分量的数量

　　例题：A喜欢B，B喜欢C，且喜欢可以传递，求所有人中有多少人被除自己以外的所有人认为是喜欢的人的数量。

　　出度为0的强连通分量y的含义是其他所有点都能到达y。

　　思路：tarjan+缩点求出来由强连通分量构成的有向无环图后，遍历图中的强连通分量，求出出度为0的强连通分量的数量。如果出度为0的强连通分量数量大于1，那么必然有一个强连通分量不被所有强连通分量联通。（出度为0的联通点不能互相到达）

//dfn表示dfs遍历到u的时间，low表示从u开始走能遍历到的最小时间戳 
int dfn[N],low[N],timestamp;    //timestamp是时间戳 
int stk[N],top; //栈 
bool in_stk[N];
//scc_cnt表示强连通块的数量，siz表示每个强连通块内的节点个数 
int dout[N],scc_cnt,siz[N],id[N];
void tarjan(int u)
{
    dfn[u]=low[u]=++timestamp;  //u的时间戳 
    stk[++top]=u,in_stk[u]=1;   //把u加入栈中 

    for(int i=h[u];i;i=e[i].ne) //遍历u的邻点 
    {
        int y=e[i].to;
        if(!dfn[y])     //y没有被遍历过 
        {
            tarjan(y);  //用dfs遍历y 
            //j也许存在反向边到达比u还高的层,所以用j能到的最小dfn序(最高点)
            //更新u能达到的(最小dfn序)最高点 
            low[u]=min(low[u],low[y]);
        }
        else if(in_stk[y])  //y在栈中说明是dfs序比当前u小，1横插边，2u的祖宗节点 
            low[u]=min(low[u],dfn[y]);  //直接用y的时间戳更新u 
    }

    if(dfn[u]==low[u])       
    {
        int y;
        scc_cnt++;      //强连通分量总数加一 
        do{
            y=stk[top--];in_stk[y]=0;
            id[y]=scc_cnt;
            siz[scc_cnt]++;     //第scc_cnt个连通块点数+1 
        }while(u!=y);

    }
}

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=m;i++)
    {
        int a,b;
        scanf("%d%d",&a,&b);
        add(a,b);
    }

    for(int i=1;i<=n;i++)
        if(!dfn[i])
            tarjan(i);

    for(int i=1;i<=n;i++)       //统计缩点之后新图的出度 
        for(int j=h[i];j;j=e[j].ne)
        {
            int y=e[j].to;
            int a=id[i],b=id[y];
            if(a!=b)dout[a]++;
        }

    int zeros=0,sum=0;  //sum存所有出度为0的强连通分量内点的个数 
    for(int i=1;i<=scc_cnt;i++)
    {
        if(!dout[i])
        {
            zeros++,sum+=siz[i];
            if(zeros>1) 
            {
                sum=0;
                break;
            }
        }
    }

    printf("%d\n",sum);

    return 0;
}

 

题型二：求有向图中强连通分量的数量，求再加几条边可以使得图中所有强连通分量互相联通

　　例题：A可以到B，B可以到C，1.问最少将信息给多少个地方，才可以使信息被所有地方知道。（求有向图中强连通分量的数量）2.问最少加几条新边，可以将信息提供给任何一个地方，其他地方都可以获得该信息（求再加几条边可以使得图中所有强连通分量互相联通）

　　思路：对于一个强连通分量，其中只要有一个地方得到了信息，那么整个分量都可以获得信息。tarjan缩点将原图转化为DAG，统计每个强连通分量的出度和入度。问题1：只要把信息给所有起点（入度为0的强连通分量）即可，答案为起点个数src。问题2：如果scc_cnt==1（只有一个强连通分量），则不需要连新边，答案是0.如果scc_cnt>1，则答案是max(src,des),即起点数量和终点数量求最大值。

 

 

int dfn[N],low[N],timestamp;
int stk[N],top,scc_cnt,id[N];
bool in_stk[N];
void tarjan(int u)
{
    dfn[u]=low[u]=++timestamp;
    stk[++top]=u;in_stk[u]=1;

    for(int i=h[u];i;i=ne[i])
    {
        int y=e[i];
        if(!dfn[y])
        {
            tarjan(y);
            low[u]=min(low[u],low[y]);
        }
        else if(in_stk[y])
            low[u]=min(low[u],dfn[y]);
    }

    if(dfn[u]==low[u])
    {
        int y;
        scc_cnt++;
        do
        {
            y=stk[top--];in_stk[y]=0;
            id[y]=scc_cnt;
        }while(y!=u);
    }

}

int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        int x;
        while(~scanf("%d",&x),x)
            add(i,x);
    }

    for(int i=1;i<=n;i++)
        if(!dfn[i])
            tarjan(i);


    for(int i=1;i<=n;i++)
        for(int j=h[i];j;j=ne[j])
        {
            int y=e[j];
            int a=id[i],b=id[y];
            if(a!=b)dout[a]++,din[b]++;
        }

    int ans1=0,ans2=0;
    for(int i=1;i<=scc_cnt;i++)
    {
        if(!din[i])ans1++;
        if(!dout[i])ans2++;
    }

    printf("%d\n",ans1);
    if(scc_cnt==1)puts("0");
    else printf("%d\n",max(ans1,ans2));


    return 0;
}