企图掌握基础背包问题
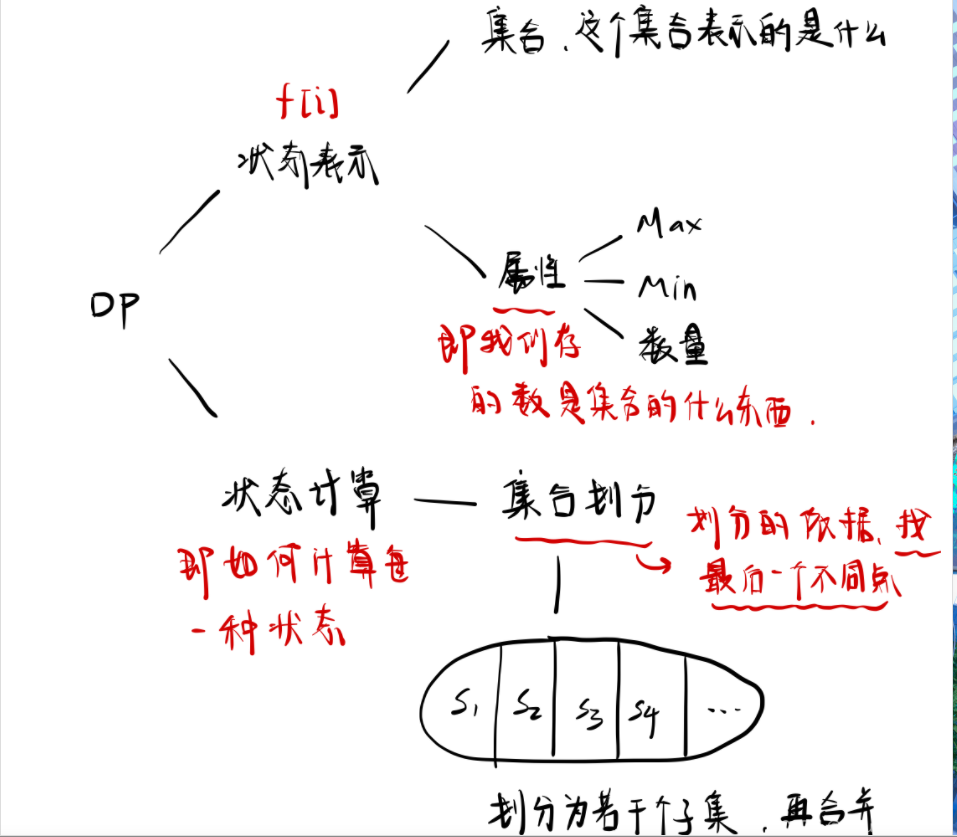
一:01背包问题
有 N件物品和一个容量是 V的背包。每件物品只能使用一次。
第 i件物品的体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
1.f [ i ] [ j ] 转化为f [ j ] 的思路:f [ i ] [ j ] 表示从前i个物品中选择,且背包容量为j时获得价值的最大值。一维下,我们少了 i 这个维度,f [ j ] 表示在前 i 轮已经决策的物品且背包容量为 j 时获得价值的最大值。因此,当循环结束后,f [ j ] 表示已经决策所有物品且背包容量为 j 的最终获得价值的最大值。
2. 01背包状态转移方程:f [ i , j ] = max(f [ i -1, j ] , f [ i - 1 , j - v [ i ] ] + w [ i ] ]
一维:f [ j ] = max ( f [ j ] , f [ j - v [ i ] + w [ i ] ]
3.一维情况下枚举背包容量要逆序:在二维情况下,状态 f [ i ] [ j ] 是由上一轮 i - 1 的状态得来的,f [ i ] [ j ] 与f [ i - 1 ] [ j ] 是独立的。而优化到一维后,如果我们还是正序,则有f [ 较小体积 ] 更新到f [ 较大体积 ] ,则有可能本应该用第 i - 1 轮的状态却用的是第 i 轮的状态。逆序是为了保证更新当前状态时,用到的状态是上一轮的状态,保证每个物品只有一次或零次;
1 #include <iostream>
2
3 using namespace std;
4
5 const int N=1e3+10;
6 int v[N],w[N];
7 int f[N];
8 int main()
9 {
10 int n,m;
11 scanf("%d%d",&n,&m);
12
13 for(int i=1;i<=n;i++)
14 scanf("%d%d",&v[i],&w[i]);
15
16
17 for(int i=1;i<=n;i++)
18 {
19 //如果j<v[i]则f[j]==上一轮的f[j] ,f[j]不需要改变
20 for(int j=m;j>=v[i];j--)
21 f[j]=max(f[j],f[j-v[i]]+w[i]);
22 }
23
24 printf("%d\n",f[m]);
25
26
27
28
29 return 0;
30 }
二:完全背包问题
有 N 种物品和一个容量是 V 的背包,每种物品都有无限件可用。
第 i 种物品的体积是 vi,价值是 wi 。
求解将哪些物品装入背包,可使这些物品的总体积不超过背包容量,且总价值最大。
1.完全背包一维时枚举背包容量不需要逆序:逆序是为了保证更新当前状态时,用到的状态是上一轮的状态,保证每个物品只有一次或零次;在完全背包中,因为每个物品可以取任意多次,所以不再强求用上一轮的状态,即本轮放过的物品,在后面还可以再放。
2.完全背包状态转移方程:f [ i , j - v [ i ] ] = max ( f [ i - 1 ] [ j ] , f [ i , j - v [ i ] + w [ i ] ]
一维:f [ j ] = max ( f [ j ] , f [ j - v [ i ] ] + w [ i ] )
1 #include <iostream>
2
3 using namespace std;
4
5 const int N=1e3+10;
6 int v[N],w[N];
7 int f[N];
8 int main()
9 {
10 int n,m;
11 scanf("%d%d",&n,&m);
12
13 for(int i=1;i<=n;i++)
14 scanf("%d%d",&v[i],&w[i]);
15
16 for(int i=1;i<=n;i++)
17 {
18 for(int j=v[i];j<=m;j++)f[j]=max(f[j],f[j-v[i]]+w[i]); //不逆序,因为物品可以用无限次
19 }
20
21 printf("%d\n",f[m]);
22
23
24
25
26 return 0;
27 }
三:多重背包问题
有 N种物品和一个容量是 V 的背包。
第 i种物品最多有 si 件,每件体积是 vi,价值是 wi。
求解将哪些物品装入背包,可使物品体积总和不超过背包容量,且价值总和最大。
1.多重背包状态转移方程:f [ i , j ] = max ( f [ i - 1, j - k * v[ i ] ] + k * w [ i ] ) ( k = 0 , 1 , . . . , si )
一维:f [ j ] = max ( f [ j ] , f [ j - v [ i ] ] + w [ i ] ) (用二进制转化为01背包问题)
2.二进制优化 O( N * V * log si ):

1 #include <iostream>
2
3 using namespace std;
4
5 const int N=3e7+100;
6 int v[N],w[N];
7 int f[N];
8 int main()
9 {
10 int n,m;
11 scanf("%d%d",&n,&m);
12
13 int cnt=0;
14 for(int i=1;i<=n;i++)
15 {
16 int a,b,s;
17 scanf("%d%d%d",&a,&b,&s);
18
19 int k=1; //组别里面的个数
20 while(k<=s)
21 {
22 v[++cnt]=a*k;w[cnt]=b*k; //整体体积与价值
23 s-=k;
24 k*=2; //组别里的个数二进制增加
25 }
26
27 if(s>0) //剩余的s单独分一组
28 {
29 v[++cnt]=a*s;w[cnt]=b*s;
30 }
31 }
32
33 for(int i=1;i<=cnt;i++) //注意枚举次数由个数n变成了组别数cnt
34 {
35 for(int j=m;j>=v[i];j--)f[j]=max(f[j],f[j-v[i]]+w[i]); //01背包
36 }
37
38 printf("%d\n",f[m]);
39
40
41
42
43 return 0;
44 }
四:分组背包问题
有 N 组物品和一个容量是 V 的背包。
每组物品有若干个,同一组内的物品最多只能选一个。
每件物品的体积是 vij,价值是 wij,其中 i 是组号,j 是组内编号。求解将哪些物品装入背包,可使物品总体积不超过背包容量,且总价值最大。
1.分组背包状态转移方程:f [ i , j ] = max ( f [ i - 1 , j ] , f [ i - 1 , j - v [ i ] [ k ] + w [ i ] [ k ] ) ( k = 1 , 2 , . . . , si )
一维:f [ j ] = max ( f [ j ] , f [ j - v [ i ][ k ] ] + w [ i ] [ k ] )
2.枚举背包容量需要逆序,因为不是无限次使用
1 #include <iostream>
2
3 using namespace std;
4
5 const int N=2e3;
6 int s[N],v[N][N],w[N][N];
7 int f[N];
8 int main()
9 {
10 int n,m;
11 scanf("%d%d",&n,&m);
12
13 for(int i=1;i<=n;i++)
14 {
15 scanf("%d",&s[i]);
16 for(int j=1;j<=s[i];j++)scanf("%d%d",&v[i][j],&w[i][j]);
17 }
18
19 for(int i=1;i<=n;i++)
20 {
21 for(int j=m;j>=0;j--) //逆序
22 {
23 for(int k=1;k<=s[i];k++)
24 {
25 if(j>=v[i][k])f[j]=max(f[j],f[j-v[i][k]]+w[i][k]);
26 }
27 }
28 }
29
30 printf("%d\n",f[m]);
31
32
33
34 return 0;
35 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号