分治法-棋盘覆盖

算法思想：分治法
实际问题：棋盘覆盖
编写语言：Java

---

问题描述

在一个 2^k×2k 个方格组成的棋盘中，恰有一个方格与其他方格不同，称该方格为一特殊方格，且称该棋盘为一特殊棋盘。在棋盘覆盖问题中，要用图示的4种不同形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格，且任何2个L型骨牌不得重叠覆盖。

Java代码

import java.util.Scanner;

public class BoardCover
{
    private static int[][] board;
    private static int num;

    //String[] 和 String... 的区别：一个是固定参数，一个是参数长度可变
    public static void main(String... args)
    {
        Scanner input = new Scanner(System.in);
        System.out.println("提示：棋盘大小必须为2的幂次方。" +
            "\n      输入的格式为：棋盘大小，特殊方格横坐标，特殊方格纵坐标" +
            "\n      分隔符为：英文逗号 + 空格，即 \", \"\n");
        System.out.print("请输入数据：");
        String aryStr = input.nextLine();
        String[] temp = aryStr.split(", ");
        int[] msg = new int[3];
        for(int i = 0; i < 3; i++)
            msg[i] = Integer.parseInt(temp[i]);
        board = new int[msg[0]][msg[0]];

        cover(msg[0], msg[1], msg[2], 0, 0);

        //给特殊点赋值
        board[msg[1]][msg[2]] = 0;
        for(int i = 0; i < msg[0]; i++)
        {
            for(int j = 0; j < msg[0]; j++)
                System.out.print(board[i][j] + " ");
            System.out.println();
        }
    }

    //参数含义：size为棋盘大小，x，y为特殊点坐标, sx，sy为棋盘起点坐标
    public static void cover(int size, int x, int y, int sx, int sy)
    {
        if(size == 1)
            return;
        int t = ++num; //函数递归的层数
        int halfSize = size / 2;

        if(x < sx + halfSize && y < sy + halfSize) //特殊点在左上角棋盘
        {
            cover(halfSize, x, y, sx, sy);
        }
        else //特殊点不在左上角棋盘
        {
            //填充右下角为特殊点
            int tx = sx + halfSize - 1;
            int ty = sy + halfSize - 1;
            board[tx][ty] = t;

            //填充剩余棋盘
            cover(halfSize, tx, ty, sx, sy);
        }

        if(x >= sx + halfSize && y < sy + halfSize) //特殊点在右上角棋盘
        {
            cover(halfSize, x, y, sx + halfSize, sy);
        }
        else //特殊点不在右上角棋盘
        {
            //填充左下角为特殊点
            int tx = sx + halfSize;
            int ty = sy + halfSize - 1;
            board[tx][ty] = t;

            //填充剩余棋盘
            cover(halfSize, tx, ty, sx + halfSize, sy);
        }

        if(x < sx + halfSize && y >= sy + halfSize) //特殊点在左下角棋盘
        {
            cover(halfSize, x, y, sx, sy + halfSize);
        }
        else //特殊点不在左下角棋盘
        {
            //填充右上角为特殊点
            int tx = sx + halfSize - 1;
            int ty = sy + halfSize;
            board[tx][ty] = t;
            //填充剩余棋盘
            cover(halfSize, tx, ty, sx, sy + halfSize);
        }

        if(x >= sx + halfSize && y >= sy + halfSize) //特殊点在右下角棋盘
        {
            cover(halfSize, x, y, sx + halfSize, sy + halfSize);
        }
        else //特殊点不在右下角棋盘
        {
            //填充左上角为特殊点
            int tx = sx + halfSize;
            int ty = sy + halfSize;
            board[tx][ty] = t;
            //填充剩余棋盘
            cover(halfSize, tx, ty, sx + halfSize, sy + halfSize);
        }
    }
}

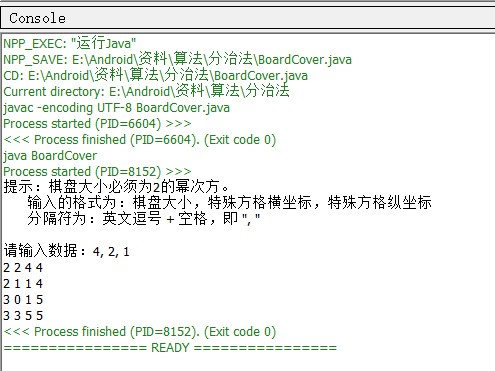
运行结果