[转]kaldi特征和模型空间转换

转：http://blog.csdn.net/shmilyforyq/article/details/76807431

博主话：这篇博客是对kaldi官网中Feature and model-space transforms in Kaldi 的翻译，因为不是专业翻译人士，接触kaldi时间也不长，所以难免有纰漏之处，希望读者如果有更好的建议和意见，可以在下面留言，有助于更好的交流，谢谢大家

介绍

Kaldi代码目前支持许多功能和模型空间的转换和预测。特征空间变换和预测以一致的方式被工具（它们在基本上只是矩阵）处理，以下部分涉及到共同点：

通常不具有说话人特征的变换，预测和其他功能操作包括：

通常以说话人自适应方式应用的全局变换是：

接下来讨论使用它们的回归类树和变换：

建立适应的回归

应用全局线性或仿射特征变换

在特征空间变换和全局投影（不与类相关联的情况下）（例如语音/不发音或回归类）的情况下，我们将它们表示为矩阵。线性变换或投影被表示为一个矩阵，通过将这个矩阵左乘以特征向量，得到变换后的特征是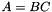 $ A x $ 。仿射变换或投影以相同的方式表示，但是我们假设1已经被附加到特征向量上，所以变换的特征是 $W \ left [\ begin {array} {c} x \\ 1 \ end {array} \ right]$ ，其中 $W = \ left [A; b \ right]$ ，A和b是线性变换和常数偏移。请注意，该约定与一些文献不同，其中1可能表现为第一维而不是最后一个维度。全局变换和投影通常以Matrix <BaseFloat类型写入单个文件，

在transform-feats中transforms 可以用来表示features。它的语法是

 transform-feats <transform> <input-feats> <output-feats>

其中<input-feats>是一个rspecifier，<output-feats>是一个wspecifier，而<transform>可能是一个rxfilename或rspecifier（请参阅指定表格式：wspecifiers和rspecifiers以及扩展文件名：rxfilenames和wxfilenames）。该程序将根据矩阵的列数是否等于特征维度，或者等于特征维度加上一个值，来确定变换是线性还是仿射。该程序通常用作管道的一部分。一个典型的例子是：

 feats="ark:splice-feats scp:data/train.scp ark:- |
          transform-feats $dir/0.mat ark:- ark:-|"
 some-program some-args "$feats" some-other-args ...

这里，文件0.mat包含单个矩阵。应用说话人特定转换的示例是：

 feats="ark:add-deltas scp:data/train.scp ark:- |
   transform-feats --utt2spk=ark:data/train.utt2spk ark:$dir/0.trans ark:- ark:-|"
 some-program some-args "$feats" some-other-args ...

一个完整的例子将如上所述，但删除了-utt2spk选项。在本例中，文件0.trans将包含由speaker-id索引的变换（例如CMLLR变换），文件数据/ train.utt2spk将具有“utt-id spk-id”形式的行（参见下一节更多的解释）。transform-feats不关心如何估计转换矩阵，它只适用于功能。在经过所有特征之后，它打印出每帧的平均对数行列式。当比较目标函数时，这可以是有用的（这个对数行列式必须被添加到像gmm-align，gmm-acc-stats或gmm-decode-kaldi这样的程序打印出来的每帧可能性上）。如果变换的线性部分A（即忽略偏移项）不是方阵，那么该程序将打印出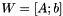 $\ frac {1} {2} \ mathbf {logdet}（AA ^ T）$ ，即伪对数行列式。当变换矩阵是MLLT矩阵乘以LDA矩阵时，对检查MLLT估计的收敛性很有用。

说话人独立与每个说话人相对于每个发音匹配

估计变换通常设置为进行特定类型的匹配，即与说话人无关的（特定说话人或语音）。例如，LDA和MLLT / STC变换是与说话人无关的，但是fMLLR变换是特定说话人或特定语音的。估计特定说话人或语音转换的程序默认情况下将按照发音模式工作，但如果提供了-spk2utt选项，则在每个说话人模式下（见下文）。

transform-feats既可以接受与说话人无关也可以接受特定说话人或语音转换。此程序检测第一个参数（变换）是否为rxfilename（请参阅扩展文件名：rxfilenames和wxfilenames）或rspecifier（请参阅指定表格式：wspecifiers和rspecifiers）。如果是前者，则将其视为与说话人无关的变换（例如，包含单个矩阵的文件）。如果后者有两个选择。如果没有提供-utt2spk选项，则将转换视为由utterance id索引的矩阵表。如果提供了一个-utt2spk选项（utt2spk是由包含speaker id的utterance索引的字符串表），那么这个变换被定为由speaker id索引。

发音到说话人和说话人到发音的映射

在这一点上，我们总结一下-utt2spk和-spk2utt选项。处理转换的程序和当你正在做每个说话人（而不是每个话语）的匹配时，都会用到它们。通常，处理已经创建的变换的程序将需要-utt2spk选项，创建转换的程序将需要-spk2utt选项。一个典型的例子是会有一个名为/ utt2spk的文件，如下所示：

spk1utt1 spk1
spk1utt2 spk1
spk2utt1 spk2
spk2utt2 spk2
...

这些字符串只是示例，它们代表通用的说话者和话语标识符; 并且会有一个名为/ spk2utt的文件，如下所示：

spk1 spk1utt1 spk1utt2
spk2 spk2utt1 spk2utt2
...

并且您将提供看起来像-utt2spk = ark： / utt2spk或-spk2utt = ark：/ spk2utt的选项。'ark：'前缀是必需的，因为这些文件由Table 代码作为rspecifier给出，并被解释为包含字符串（或者在spk2utt情况下的字符串向量）的归档。请注意，utt2spk通常以随机访问方式访问，因此，如果正在处理数据子集，则可以安全地提供整个文件，spk2utt通常以顺序的方式访问，因此，如果使用数据子集你将要拆分spk2utt。

接受spk2utt选项的程序通常会遍历spk2utt文件中的speaker-id，并且对于每个speaker-id，它们将遍历每个演讲者的话语（utterances），累加每个话语的统计信息。然后访问特征文件将处于随机访问模式，而不是正常的顺序访问。这需要设置一些注意事项，因为特征文件相当大，并且fully-processed 的特征通常要从存档读取（如果不仔细设置，则不允许最高效的内存随机访问）。为了避免在这种情况下访问功能文件时出现内存膨胀，建议确保所有归档按照utterance-id进行排序，提供给-spk2utt选项的文件中的说话按排序顺序显示，并且在指定向这些程序输入的特征的rspecifier中给出了适当的选项（例如“ark，s，cs： - ”，如果它是标准输入）。请参阅 Avoiding memory bloat when reading archives in random-access mode ，以便进一步讨论此问题。

组合变换

另一个接受泛型变换的程序是compose-transforms。一般语法是“compose-transforms a b c”，它执行乘法c = ab（如果a是仿射，则比矩阵乘法多一点运算量）。从脚本修改的示例如下：

 feats="ark:splice-feats scp:data/train.scp ark:- |
         transform-feats
           \"ark:compose-transforms ark:1.trans 0.mat ark:- |\"
           ark:- ark:- |"
 some-program some-args "$feats" ...

该示例还说明了使用从程序调用的两个级别的命令。这里，0.mat是一个全局矩阵（例如LDA），而1.trans是一组由utterance id索引的fMLLR / CMLLR矩阵。compose-transforms将转换组合在一起。相同的特征可以更简单地计算，但是效率较低，如下所示：

 feats="ark:splice-feats scp:data/train.scp ark:- |
         transform-feats 0.mat ark:- ark:- |
         transform-feats ark:1.trans ark:- ark:- |"
 ...

通常，作为组合变换的输入的变换a和b可以是与说话人无关的变换或特定说话人或语音的变换。如果a是特定语音的，b是特定说话人的，那么你必须提供-utt2spk选项。然而，不支持如果a是特定语音的，b是特定说话人的组合（当然这也没有太大意义）。如果a或b是tables，组合转换的输出将是一个table。三个参数a，b和c可以代表table或正常文件（即{r，w}specifiers或{r，w} xfilenames），但须符合一致性要求。

如果a是仿射变换，为了正确地执行组合，组合变换需要知道b是仿射还是线性（它不知道，因为它不能访问由b转换的特征的维度）。这由选项-b-is-affine（bool，default false）控制。如果b是仿射的，但是您忘记设置此选项，并且a是仿射，则组合转换将b看做是实际输入特征维度加1的线性变换，并将输出实际输入特征维度加2的变换。当转换功能应用于特征时，没有办法用“transform-feats”来解释这一点，所以在这一点上，错误应该变得明显。

估计变换时的静音权重

估计说话人自适应变换（如CMLLR）时，消除静音帧是非常有用的。当使用回归树的多类方法（参见构建回归树进行适应）时，这似乎也是正确的。我们实现这一点的方式是通过降低与静音音素相关的后验概率，这相当于对状态水平后验概率的改善。下面提供了一个bash shell脚本的一部分（此脚本在Global CMLLR / fMLLR转换中有更详细的讨论）：

ali-to-post ark:$srcdir/test.ali ark:- | \
  weight-silence-post 0.0 $silphones $model ark:- ark:- | \
  gmm-est-fmllr --fmllr-min-count=$mincount \
    --spk2utt=ark:data/test.spk2utt $model "$sifeats" \
   ark,o:- ark:$dir/test.fmllr 2>$dir/fmllr.log

这里，shell变量“silphones”将被设置为无声电话的整数id的冒号分隔列表。

线性判别分析（LDA）转换

Kaldi通过LdaEstimate类支持LDA估计。该类不直接与任何特定类型的模型交互; 它需要使用类的数量进行初始化，累加函数被声明为：

class LdaEstimate {
  ...
  void Accumulate(const VectorBase<BaseFloat> &data, int32 class_id,
                  BaseFloat weight=1.0);
};

程序acc-lda将声学状态（即pdf-id）作为类来累计LDA统计量。它需要转换模型，以便将对齐（以transition-id表示）与pdf-id进行映射。然而，它不限于特定类型的声学模型。

est-lda是LDA估计（它读入acc-lda的统计数据）。从变换中获得的特征将具有单位方差，但不一定为零。程序est-lda输出LDA变换矩阵，并且使用选项-write-full-matrix可以写出没有降维的完整矩阵（其第一行将等效于LDA投影矩阵）。当使用LDA作为HLDA的初始化时，这可能很有用。

框架拼接

通常在LDA之前对原始MFCC特征进行帧拼接（例如，将九个连续的帧拼接在一起）。程序splice-feats这样做。使用此脚本的典型行如下：

feats="ark:splice-feats scp:data/train.scp ark:- |
        transform-feats $dir/0.mat ark:- ark:-|"

并且“feats”变量稍后将被某些需要读取功能的程序用作rspecifier（参见指定表格式：wspecifiers和rspecifiers）。在这个例子中，因为我们使用默认值（-left上下文= 4，右上下文= 4，总共9个帧），我们没有指定拼接在一起的帧数。

Delta特征计算

delta功能的计算由程序add-deltas完成，它使用ComputeDeltas函数。delta特征计算具有与HTK相同的默认设置，即，通过值[-2，-1,0,1,2]的滑动窗口来计算乘以特征的第一个增量特征，然后通过除以（2 ^ 2 + 1 ^ 2 + 0 ^ 2 + 1 ^ 2 + 2 ^ 2 = 10）。通过对第一个增量特征应用相同的方法来计算第二个增量特征。每一边上下文的帧数由-delta-window（默认值：2）控制，并且要添加的增量特征数由-delta-order（默认值：2）控制。使用这种方式的典型脚本行是：

feats =“ark：add-deltas --print-args = false scp：data / train.scp ark： -  |”

异方差线性判别分析（HLDA）

HLDA是使用最大似然估计的降维线性特征投影，其中使用全局平均值和方差对“被拒绝”维度进行建模，并且“接受的”维度用特征模型建模，其均值和方差是通过最大似然估计的。目前与工具集成的HLDA的形式在HldaAccsDiagGmm中实现。使用相对紧凑的统计形式来估计GMM的HLDA，这些类对应于模型中的高斯。由于它不使用标准估计方法，我们将在此解释这个想法。首先，由于内存限制，我们不想存储HLDA统计量（每个类的平均值和全协方差统计）的最大形式。我们观察到，如果在HLDA更新阶段，我们将方差保持固定，则HLDA估计的问题将降低到MLLT（或全局STC）估计问题。参见“用于隐马尔可夫模型的半绑合协方差矩阵”，由Mark Gales，IEEE Transactions on Speech and Audio Processing，vol。7，1999，第272-281页，例如等式（22）和（23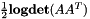）。 $\ mathbf {G} ^ {（ri）}$ 统计量也在这里使用，但是在HLDA案例中，需要对被接受和拒绝的维度进行稍微不同的定义。假设原始特征维度为D，缩小的特征维数为K。我们先忽略迭代上标r，并将下标j用于表示状态，m表示高斯混合数。对于可接受的维度（ $0 \ leq i <K$ ），统计量为：

$\ [\ mathbf {G} ^ {（i）} = \ sum_ {t，j，m} \ gamma_ {jm}（t）\ frac {1} {\ sigma ^ 2_ {jm}（i） mu_ {jm} - \ mathbf {x}（t））（\ mu_ {jm} - \ mathbf {x}（t））^ T \]$

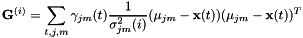其中 $\ mu_ {jm} \ in \ Re ^ {K}$ 原始D维空间中的高斯均值，并且 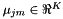$\ mathbf {X}（t）的$ 是原始K维空间中的特征，但是 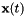$\西格玛^ 2_8 {} JM（我）$ K维模型内的方差的第i维。

对于被拒绝的维度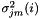（ $K \ leq d <D$ ），我们使用单位方差高斯，统计量如下：

$\ [\ mathbf {G} ^ {（i）} = \ sum_ {t，j，m} \ gamma_ {jm}（t）（\ mu - \ mathbf {x}（t））（\ mu - \ mathbf {x}（t））^ T，\]$

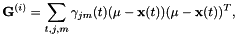其中 $$ \ $万亩$ 表示在K维空间中的全局特征均值。一旦我们得到这些统计量，HLDA估计与维D中的MLLT / STC估计相同。注意，所有拒绝维度的 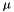$\ mathbf {G}$ 统计量是相同的，因此在代码中，我们仅存储K + 1维而不是D维的统计量。

此外，对于积累统计量的程序来说，只用访问K维模型很方便，所以在HLDA累加过程中，我们积累了足够的统计量来估计K维平均值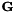 $\ {mu_ JM}$ ，而不是G我们积累的统计数据如下：

对于接受维度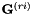（ $0 \ leq i <K$ ），

$\ [\ mathbf {S} ^ {（i）} = \ sum_ {t，j，m} \ gamma_ {jm}（t）\ frac {1} {\ sigma ^ 2_ {jm}（i）} \ mathbf {x}（t）\ mathbf {x}（t）^ T \]$

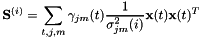
对于拒绝维度 $K \ leq i <D$

$\ [\ mathbf {S} ^ {（i）} = \ sum_ {t，j，m} \ gamma_ {jm}（t）\ mathbf {x}（t）\ mathbf {x}（t） \]$

当然，我们只需要存储其中的一个（例如，对于i = K），因为它们都是一样的。然后在更新时间，我们可以计算维度为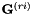 $0 \ leq i <K$ 的G统计量：

$\ [\ mathbf {G} ^ {（i）} = \ mathbf {S} ^ {（i）} - \ sum_ {j，m} \ gamma_ {jm} \ mu_ {jm} \ mu_ {jm} ^ T ，\]$

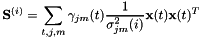对于 $K \ leq i <D$ ，

$\ [\ mathbf {G} ^ {（i）} = \ mathbf {S} ^ {（i）} - \ beta \ mu \ mu ^ T，\]$

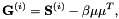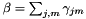其中 $\ beta = \ sum_ {j，m} \ gamma_ {jm}$ 是总数， $\ mu = \ frac {1} {\ beta} \ sum_ {j，m} \ mu_ {j，m}$ 是全局特征的均值。在使用与MLLT相同的计算方法从G统计量计算变换后，我们输出变换，并且还使用变换的第一个K行将均值投影到维K中，并写出变换后的模型。

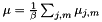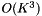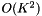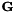这里描述的计算过程相当缓慢; 每个框架上的复杂度是 $ O（K ^ 3）$ ，K也非常大（例如117）。这是我们为紧凑统计所付出的代价; 如果我们存储完整的均值和方差统计量，则每帧计算复杂度将是 $ O（K ^ 2）$ 。为了加快速度，我们有一个可选参数（代码中的“speedup”），它可以选择一个随机的帧子集来计算HLDA统计量。例如，如果speedup = 0.1，我们只会在1/10的帧上累加HLDA统计量。如果此选项被激活，我们需要存储关于均值统计量的两个不同版本。一个版本的均值统计量，是在子集统计的，只能用于HLDA运算，其值对应着公式中的 $\ {gamma_ JM}$ 和 $\ {mu_ JM}$ 。另一个版本的均值统计量是由全部训练数据统计的，可以写出转换模型。

整体HLDA估计过程如下（见rm_recipe_2 / scripts / train_tri2j.sh）：

首先用LDA初始化它（我们存储缩减维矩阵和全矩阵）。
开始模型建立和训练过程。在我们决定进行HLDA更新的某些（非连续）迭代中，执行以下操作：
- 累加HLDA统计量（S，加上全维度均值统计量）。积累这些（gmm-acc-hlda）的程序需要模型，未转换的特征和当前的变换（它需要转换特征才能计算高斯验概率）
- 更新HLDA变换。这样做的程序（gmm-est-hlda）需要模型; 统计量; 和先前的全（平方）转换矩阵，它需要开始优化并正确地报告辅助功能变化。它输出新的变换（全部和缩小的维度），以及新的估计和转换均值的模型。

全局半绑定协方差（STC）/最大似然线性变换（MLLT）估计

全局STC / MLLT是一个特征变换方阵。有关更多细节，请参见"Semi-tied Covariance Matrices for Hidden Markov Models", by Mark Gales, IEEE Transactions on Speech and Audio Processing, vol. 7, 1999, pages 272-281.将其视为特征空间变换，目标函数是给定模型的变换特征的平均每帧对数似然，加上变换的对数行列式。模型的均值也在更新阶段通过变换旋转。足够的统计量如下，对于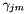 $0 \ leq我<D$ ，其中D是特征维度：

$\ [\ mathbf {G} ^ {（i）} = \ sum_ {t，j，m} \ gamma_ {jm}（t）\ frac {1} {\ sigma ^ 2_ {jm}（i） mu_ {jm} - \ mathbf {x}（t））（\ mu_ {jm} - \ mathbf {x}（t））^ T \]$

有关更新方程，请参考等式（22）和（23）。这些基本上是对角线逐行约束MLLR / fMLLR更新方程的简化形式，其中二次方程的一阶项消失。请注意，我们的实现与参考的不同之处在于使用矩阵的逆矩阵而不是代数余子式，因为乘以行列式不会对结果产生影响，并且可能会导致浮点下溢或溢出的问题。

我们描述一下在LDA特征之上进行MLLT全过程，但它也适用于传统的差分特征。请参阅脚本rm_recipe_2 / steps / train_tri2f作为示例。过程如下：

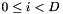估计LDA转换矩阵（我们只需要它的第一行，而不是整个矩阵）。调用这个矩阵 $\ mathbf {M}$ 。
启动正态模型构建过程，始终使用转换的特征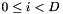。在某些选定的迭代过程（我们将更新MLLT矩阵）中，我们执行以下操作：
- 在当前完全转换的空间（即，与之相关的特征之上 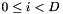$\ mathbf {M}$ ）累计MLLT统计量。为了提高效率，我们使用训练数据的一部分来实现。
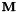- 做MLLT更新; 让它产生一个方阵 $\ mathbf {T】$ 。
- 通过设置 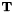$\ mu_ {jm} \ leftarrow \ mathbf {T} \ mu_ {jm}$ 来转换模型。
- 通过设置 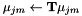$\ mathbf {M} \ leftarrow \ mathbf {T} \ mathbf {M}$ 更新当前的变换

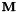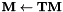涉及MLLT估计的程序是gmm-acc-mllt和est-mllt。我们还需要程序gmm-transform-means（使用 $\ mathbf {T】$ 转换高斯函数均值），compose-transforms（做乘法 $\ mathbf {M} \ leftarrow \ mathbf {T} \ mathbf {M}$ ）。

全局CMLLR / fMLLR转换

约束最大似然线性回归（CMLLR），也称为特征空间MLLR（fMLLR），是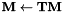 $\ mathbf {x} \ rightarrow \ mathbf {A} \ mathbf {x} + \ mathbf {b}$ 的仿射特征变换，也可以 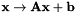$\ mathbf {x} \ rightarrow \ mathbf {W} \ mathbf {x} ^ +$ 表示，其中 $\ mathbf {x} ^ + = \ left [\ begin {array} {c} \ mathbf {x} \\ 1 \ end {array} \ right]$ 。请注意，这不同于文献中的1在最前面。

关于CMLLR和我们使用的估计技术的综述文章，参见"Maximum likelihood linear transformations for HMM-based speech recognition" by Mark Gales, Computer Speech and Language Vol. 12, pages 75-98.

我们存储的足够统计量是：

$\ [\ mathbf {K} = \ sum_ {t，j，m} \ gamma_ {j，m}（t）\ Sigma_ {jm} ^ { - 1} \ mu_ {jm} \ mathbf {x}（t） ^ + \]$

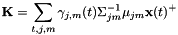其中 $\ {Sigma_ JM} ^ { - 1}$ 是逆协方差矩阵，而对于 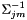$0 \ leq我<D$ 其中D是特征维度，

$\ [\ mathbf {G} ^ {（i）} = \ sum_ {t，j，m} \ gamma_ {j，m}（t）\ frac {1} {\ sigma ^ 2_ {j，m} ）} \ mathbf {x}（t）^ + \ left。\ mathbf {x}（t）^ + \ right。^ T \]$

我们的估计方案是标准的，参见参考文献的附录B（特别是B.1节“Direct method over rows”）。我们不同的是使用逆矩阵的一列而不是代数余子式的行，即忽略行列式的因素，因为它不影响结果并引起数字下溢或溢出的危险。

全局约束MLLR（CMLLR）转换的估计由类FmllrDiagGmmAccs和程序gmm-est-fmllr完成（另见gmm-est-fmllr-gpost）。gmm-est-fmllr的语法是：

gmm-est-fmllr [options] <model-in> <feature-rspecifier> \
   <post-rspecifier> <transform-wspecifier>

“<post-rspecifier>”项目对应于transition-id 级别的后验概率（参见 State-level posteriors）。该程序写出一个默认由utterance索引的CMLLR变换表，或者如果给出了-spk2utt选项，则由说话者索引。

以下是脚本的简化摘录（rm_recipe_2 / steps / decode_tri_fmllr.sh），它基于来自先前的unadapted的解码的对齐来估计和使用CMLLR变换。假设以前的解码是使用相同的模型（否则我们必须使用程序“convert-ali”来转换对齐方式）。

...
silphones=48 # colon-separated list with one phone-id in it.
mincount=500 # min-count to estimate an fMLLR transform
sifeats="ark:add-deltas --print-args=false scp:data/test.scp ark:- |"

# The next comand computes the fMLLR transforms.
ali-to-post ark:$srcdir/test.ali ark:- | \
  weight-silence-post 0.0 $silphones $model ark:- ark:- | \
  gmm-est-fmllr --fmllr-min-count=$mincount \
    --spk2utt=ark:data/test.spk2utt $model "$sifeats" \
   ark,o:- ark:$dir/test.fmllr 2>$dir/fmllr.log

feats="ark:add-deltas --print-args=false scp:data/test.scp ark:- |
  transform-feats --utt2spk=ark:data/test.utt2spk ark:$dir/test.fmllr
       ark:- ark:- |"

# The next command decodes the data.
gmm-decode-faster --beam=30.0 --acoustic-scale=0.08333 \
  --word-symbol-table=data/words.txt $model $graphdir/HCLG.fst \
 "$feats" ark,t:$dir/test.tra ark,t:$dir/test.ali 2>$dir/decode.log

线性VTLN（LVTLN）

近年来，已经有许多论文描述了声道长度归一化（VTLN）的实现，该方法计算出对应于每个VTLN弯折因子的线性特征变换。参见``Using VTLN for broadcast news transcription'', by D. Y. Kim, S. Umesh, M. J. F. Gales, T. Hain and P. C. Woodland, ICSLP 2004.

我们使用LinearVtln类实现了这个一般类中的一个方法，以及诸如gmm-init-lvtln，gmm-train-lvtln-special和gmm-est-lvtln-trans之类的程序。所述LinearVtln对象本质上存储一组线性特征变换，每个对应着一个弯折因子。让这些线性特征变换矩阵为

$\ [\ mathbf {A} ^ {（i）}，0 \ leq i <N，\]$

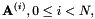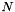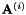其中例如我们可能 $ N $ = 31，对应于31个不同的弯折因子。我们将在下面描述我们如何获得以下这些矩阵。估计说话人特定变换的方式如下。首先，我们需要某种模型和相应的对齐方式。在示例脚本中，我们使用小型单音素模型，或使用完整的三音素模型。从这个模型和对齐方式，并使用原始的，未弯折的特征，我们计算用于估计CMLLR的常规统计量。要计算LVTLN变换，需得到每个矩阵 $\ mathbf {A} ^ {（I）}$ ，并计算使变换 $\ mathbf {W} = \ left [\ mathbf {A} ^ {（i）} \，; \，\ mathbf {b} \ right]$ 的CMLLR辅助函数最大化的偏移向量 $\ mathbf {B}$ 。给出最大辅助函数值（即最大化i）的 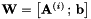$\ mathbf {白}$ 值成为该说话人的变换（译者注：不太确定，附上原文 This value of 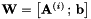$\mathbf{W}$ that gave the best auxiliary function value (i.e. maximizing over i) becomes the transform for that speaker）。由于我们在这里估计一个均值偏移量，所以我们基本上将一种基于模型的倒谱平均归一化（或者是仅偏移的CMLLR形式）与作为线性变换实现的VTLN曲折率（warping ）相结合。这避免了只有均值规范化这一个步骤。

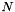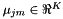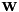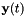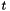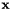我们接下来描述我们如何估计矩阵 $\ mathbf {A} ^ {（I）}$ 。我们不按照参考文献中所述的相同方式，我们的方法更简单（更容易证明）。这里我们只说一个特定的弯折因子的计算; 在目前的脚本中，我们有不同的弯折因子，从0.85，0.86，...，1.15。我们采用特征数据的一个子集（例如数十个话语），对于这个子集，我们计算原始和变换的特征，其中使用常规的VLTN计算来计算变换后的特征（参见特征级声道长度归一化（VTLN ））。调用原始和转换的特征分别是 $\ mathbf {X}（t）的$ 和 $\ mathbf {Y}（t）的$ ，其中 $ T $ 的取值范围是所选语音的帧。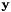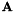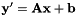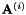我们计算最小二乘法意义上的从 $\ mathbf {X}$ 映射到 $\ mathbf {Y}$ 的仿射变换，即如果 $\ mathbf {y}'= \ mathbf {A} \ mathbf {x} + \ mathbf {b}$ 我们计算使 $\ sum_t（\ mathbf {y}'（t） - \ mathbf {y}（t））^ T（\ mathbf {y}'（t） - \ mathbf {y}（t））$ 最小的 $\ mathbf {A}$ 和 $\ mathbf {B}$ 。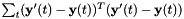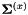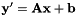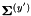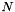然后，我们归一化对角方差如下：我们计算的原始特征方差 $\ mathbf {\西格玛} ^ {（X）}$ 和线性变换特征方差 $\ mathbf {\西格玛} ^ {（Y'）}$ ，并且对于每个d，都将 $\ mathbf {A}$ 的第d行乘以 $\ sqrt {\ frac {\ mathbf {\ Sigma} ^ {（x）} _ {d，d}} {\ mathbf {\ Sigma} ^ {（y'）} _ {d，d}}}$ ，得到的矩阵就是 $\ mathbf {A} ^ {（I）}$ 。

命令行工具支持在评估要使用的变换矩阵时忽略对数行列式的选项（例如，可以设置-logdet-scale = 0.0）。在某些情况下，这似乎会改善结果; 忽略对数决定因素，它总是使得弯折因子的分布更加双峰，因为对数行列式不是正的，只是在弯折因子为1.0时为0，因此对数行列式相当于惩罚项为了使弯折因子不远离1。然而，对于某些类型的特征（特别是从LDA导出的特征），忽略对数行列式使得结果变得更糟，并导致非常奇怪的弯折因子分布，因此我们的示例脚本始终使用对数行列式。无论如何，这是正确的事情。

内部C ++代码支持对变换矩阵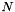 $\ mathbf {A} ^ {（I）}$ 的最大似然重估计的累积统计。我们的期望这样会改善结果。然而，它导致性能下降，所以我们不包括这样做的示例脚本。

指数变换（ET）

指数变换（ET）是计算VTLN类变换的另一种方法，但与线性VTLN不同，我们完全切断与频率弯折的连接，并以数据驱动的方式学习。对于正常的训练数据，我们发现它的学习与传统的VTLN非常相似。

ET是一种转换形式：

$\ [\ mathbf {W} _s = \ mathbf {D} _s \ exp（t_s \ mathbf {A}）\ mathbf {B}，\]$

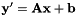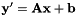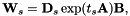其中exp是通过 $\ mathbf {A}$ 的泰勒级数定义的矩阵指数函数，与标量指数函数一样。具有下标“s”的值是说话人特定的; 其他数量（即 $\ mathbf {A}$ 和 $\ mathbf {B}$ ）是全局的，并在所有说话人之间共享。

这个方程中最重要的因子是中间的指数函数。因子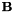 $\ mathbf {D} _s$ 整合基于模型的均值和可选的方差归一化（即仅偏移或仅对角话的CMLLR），因子 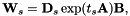$\ mathbf {B}$ 允许变换到MLLT（也称为全局STC），也是在每次重新估计的迭代中重新归一化 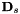$t_s$ 的副产物。这些因子的维度如下，其中D是特征的维度：

$\ \ \ mathbf {D} _s \ in \ Re ^ {D \ times（D + 1）}，\ t_s \ in \ Re，\ \ mathbf {A} \ in \ Re ^ {（D + 1）\ times （D + 1）}，\ \ mathbf {B} \ in \ Re ^ {（D + 1）\ times（D + 1）}。 \]$

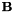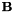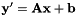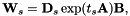请注意，如果 $\ mathbf {D} _s$ 是一个完全无约束的CMLLR矩阵，那么这个方法就没有意义，因为方程式中的其他因子不会增加自由度。这些工具支持对 $\ mathbf {D} _s$ 的三种约束：它可以是 $[{\ mathbf I} \，\; \，{\ mathbf 0}]$ （无适应），或 $[{\ mathbf I} \，\; \，{\ mathbf m}]$ （仅偏移）或 ${{\ mathrm {diag}}（{\ mathbf d}）\，\; \，{\ mathbf m}]$ （对角CMLLR）; 这由命令行工具的-normalize-type选项控制。 $\ mathbf {A}$ 的最后行和 $\ mathbf {B}$ 被固定在特定的值（这些行参与与值1.0，它被附加到特征，以表达一个仿射变换作为基质中传播的最后一个载体元件）。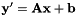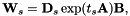最后一行 $\ mathbf {A}$ 固定为零， $\ mathbf {B}$ 的最后一行固定为 $[0 \ 0 \ 0 \ \ ldots \ 0 \ 1]$ 。

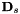说话人特定量 $ T_S $ 可以被解释为说话人特定的弯折因子的对数。使用指数函数是因为，如果先被因子f弯折然后被因子g弯折，弯折度应该与组合因子fg的相同。令l = log（f），m = log（g）。然后我们通过定义证明这个性质

$\ [\ exp（l \ mathbf {A}）\ exp（m \ mathbf {A}）= \ exp（（l + m）\ mathbf {A}）。 \]$

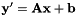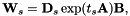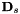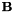特定说话人的ET计算如下：这假设给定 $\ mathbf {A}$ 和 $\ mathbf {B}$ 。并累计每个说话人的足够的常规CMLLR统计量。在更新阶段，我们迭代优化 $ T_S $ 和 $\ mathbf {D} _s$ 使辅助函数（ auxiliary function）最大化。用基于牛顿法的迭代过程来更新 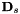$ T_S $ ; 用基于传统的CMLLR方法来更新 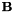$\ mathbf {D} _s$ ，特别的关于对角线或仅偏移的情况，我们通过对 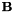$\ mathbf {D} _s$ 的约束来实现。

整体训练计算如下：

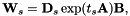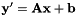首先，初始化 $\ mathbf {B}$ 为id， $\ mathbf {A}$ 为最后一行为零的随机矩阵。

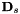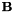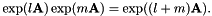然后，从一些已知的模型开始，开始迭代 EM过程。在每次迭代中，我们首先估算特定说话人的参数 $ T_S $ 和 $\ mathbf {D} _s$ ，并计算变换 $\ mathbf {白} _s$ ，然后我们选择更新 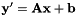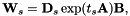$\ mathbf {A}$ 、 $\ mathbf {B}$ 和模型三者中的一个。

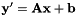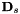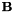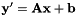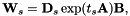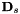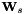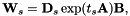如果更新 $\ mathbf {A}$ ，则固定给定和 $\ mathbf {D} _s$ 。这个更新不能保证收敛，但在实践中迅速收敛; 它基于二次“弱感辅助功能（weak-sense auxiliary function）”，其中使用矩阵指数函数的泰勒级数展开的一阶截断来获得二次项。更新 $\ mathbf {A}$ 后，我们将修改 $\ mathbf {B}$ 使重新归一化到0，使 $\ exp（t \ mathbf {A}）$ 左乘 $\ mathbf {B}$ ，其中t是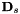的平均值。
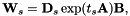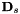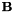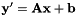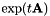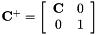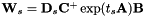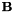如果更新 $\ mathbf {B}$ ，也是固定给定和 $\ mathbf {D} _s$ ，并且更新类似于MLLT（也称为全局STC）。为了累计和更新，想象估计MLLT矩阵是矩阵 $\ mathbf {A}$ 的左边，如 $\ mathbf {C} \ in \ Re ^ {D \ times D}$ ，定义 $\ mathbf {C} ^ + = \ left [\ begin {array} {cc} \ mathbf {C}＆0 \\ 0＆1 \ end {array} \ right]$ ，变换变成 $\ mathbf {W} _s = \ mathbf {D} _s \ mathbf {C} ^ + \ exp（t_s \ mathbf {A}）\ mathbf {B}$ 。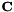在概念上，在估计 $\ mathbf {C}$ 时，我们把 $\ mathbf {D} _s$ 当做创建说话者特定的模型空间变换，这是唯一可能的 $\ mathbf {D} _s$ 对角线结构; 并且将 $\ exp（t_s \ mathbf {A}）\ mathbf {B}$ 视为特征空间变换（即作为特征的一部分）。估计 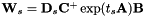$\ mathbf {C}$ 后，我们将使用定义
$\ [\ mathbf {C} ^ + \ exp（t_s \ mathbf {A}）= \ exp（t_s \ mathbf {C} ^ + \ mathbf {A} \ left。\ mathbf {C} ^ + \ right。 {-1}）\ mathbf {C} ^ + \]$
所以更新成为：
$\ [\ mathbf {A} \ leftarrow \ mathbf {C} ^ + \ mathbf {A} \ left。\ mathbf {C} ^ + \ right。^ { - 1}，\ \ \ mathbf {B} \ leftarrow \ mathbf {C} ^ + \ mathbf {B}。 \]$
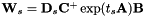在这一点上，我们需要用矩阵来转换模型 $\ mathbf {C}$ 。读者可能会对估计 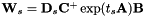$\ mathbf {C}$ 时那些因子如何相互作用的有疑惑，我们将数量 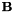$\ mathbf {D} _s$ 视为模型空间变换。如果 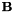$\ mathbf {D} _s$ 只包含一个均值偏移，我们仍然可以证明辅助函数会增加，除非我们必须适当地改变偏移量（这样做不好，因为我们将在下一次迭代中重新估计它们）。然而，如果 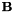$\ mathbf {D} _s$ 有非单元对角线（即有对角但没有CMLLR偏移），则不能保证这种重估计过程能够提高似然性; 在这种情况下，工具将会打印一个警告。为了避免遇到这种情况，我们的脚本以一种 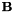$\ mathbf {D} _s$ 仅偏移转换的模式进行训练;但是在测试中我们允许 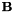$\ mathbf {D} _s$ 为对角CMLLR变换时，结果比只偏移的要好一丢丢。
更新模型很简单; 它只涉及适应了的特征的训练。

与使用指数变换相关的重要程序如下：

gmm-init-et 初始化指数变换对象（包含A和B）并将其写入磁盘; A的初始化是随机的。
gmm-est-et 估计一组说话人的指数变换; 它读取指数变换对象，模型，特征和高斯层的后验概率，并写出变换 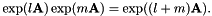$\ mathbf {白} _s$ 和可选的“扭曲因子” 。
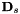gmm-et-acc-a 累积更新的统计数据 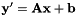$\ mathbf {A}$ ，gmm-et-est-a进行相应的更新。
gmm-et-acc-b 积累更新的统计数据 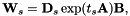$\ mathbf {B}$ ，gmm-et-est-b进行相应的更新。

倒谱平均值和方差归一化

倒谱平均值和方差归一化包括对原始cepstra的平均值和方差进行归一化，通常以发音（utterance）或每个说话人为基础，给出零均值，单位方差cepstra。我们提供代码来支持这一点，还有一些示例脚本，但我们并不特别推荐使用它。一般来说，我们更喜欢基于模型的方法来表示均值和方差归一化; 例如，线性VTLN（LVTLN）学习平均偏移量和指数变换（ET）执行对角CMLLR变换，其具有与倒谱平均值和方差归一化相同的功率（通常应用于完全扩展的特征）。对于非常快速的操作，可以在基于发音的非常小的语言模型使用这个方法，我们的一些示例脚本演示了这一点。特征提取代码中也可以在每个语音（utterance）的基础上减去平均值（计算-mfcc-feats和compute-plp-feats的-subtract-mean选项）。

为了支持每个语音和每个说话人的均值和方差归一化，我们提供程序compute-cmvn-stats和apply-cmvn。默认情况下，程序compute-cmvn-stats将计算均值和方差归一化的足够统计量，作为一个矩阵（格式不是很重要;详见代码），并将写出用utterance-id索引的统计量。如果给出-spk2utt选项，它将以每个演讲者的方式写出统计量（警告：在使用此选项之前，请阅读在随机访问模式下读取归档时避免内存膨胀，因为此选项会导致输入功能以随机访问模式读取）。程序“apply-cmvn”读入特征和倒谱均值和方差统计; 如果应用了-utt2spk选项，则默认情况下，每个话语的统计量都将被索引（或者每个说话人进行索引）。它在均值和方差归一化之后写出特征。尽管有这些名称，这些程序并不在意，这些功能是由cepstra还是其他任何东西组成; 它只是将它们视为矩阵。当然，给定的ecompute-cmvn-stats和apply-cmvn函数必须具有相同的维度。

我们注意到，它可能与特征变换代码的整体设计更一致，提供一个版本的compute-cmvn-stats，它将平均和方差归一化变换以通用仿射变换（与CMLLR转换格式一样）的形式写出，以便它们可以被程序transform-feats调用，并根据需要和compose-transforms的变换进行组合。如果需要，我们可能会提供这样一个程序，但是由于我们不把平均值和方差归一化作为任何方法的重要组成部分，我们还没有这样做。

建立适应的回归树

Kaldi支持回归树MLLR和CMLLR（也称为fMLLR）。有关回归树的概述，请参见 "The generation and use of regression class trees for MLLR adaptation" by M. J. F. Gales, CUED technical report, 1996。

东西有点多，后面慢慢理解

posted @ 2017-09-13 17:06 WELEN 阅读(3243) 评论(0) 编辑收藏举报

刷新页面返回顶部

WELEN