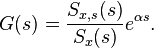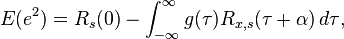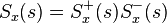心胸决定格局，眼界决定境界...

基于winner 滤波平稳降噪效果

https://en.wikipedia.org/wiki/Wiener_filter

Wiener filter solutions

The Wiener filter problem has solutions for three possible cases: one where a noncausal filter is acceptable (requiring an infinite amount of both past and future data), the case where a causal filter is desired (using an infinite amount of past data), and the finite impulse response (FIR) case where a finite amount of past data is used. The first c

ase is simple to solve but is not suited for real-time applications. Wiener's main accomplishment was solving the case where the causality requirement is in effect, and in an appendix of Wiener's book Levinson gave the FIR solution.

Noncausal solution

G(s) = \frac{S_{x,s}(s)}{S_x(s)}e^{\alpha s}.

Where  S are spectra. Provided that  g(t) is optimal, then the minimum mean-square error equation reduces to

E(e^2) = R_s(0) - \int_{-\infty}^{\infty}{g(\tau)R_{x,s}(\tau + \alpha)\,d\tau},

and the solution  g(t) is the inverse two-sided Laplace transform of  G(s).

Causal solution

G(s) = \frac{H(s)}{S_x^{+}(s)},

where

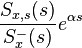  • H(s) consists of the causal part of  \frac{S_{x,s}(s)}{S_x^{-}(s)}e^{\alpha s} (that is, that part of this fraction having a positive time solution under the inverse Laplace transform)
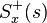  • S_x^{+}(s) is the causal component of  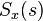S_x(s) (i.e., the inverse Laplace transform of  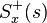S_x^{+}(s) is non-zero only for  t \,\ge\, 0)
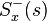  • S_x^{-}(s) is the anti-causal component of  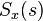S_x(s) (i.e., the inverse Laplace transform of  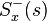S_x^{-}(s) is non-zero only for  t < 0)

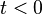This general formula is complicated and deserves a more detailed explanation. To write down the solution  G(s) in a specific case, one should follow these steps:[2]

  1. Start with the spectrum 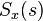 S_x(s) in rational form and factor it into causal and anti-causal components:
    S_x(s) = S_x^{+}(s) S_x^{-}(s)
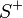    where  S^{+} contains all the zeros and poles in the left half plane (LHP) and  S^{-} contains the zeroes and poles in the right half plane (RHP). This is called the Wiener–Hopf factorization.
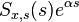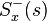  2. Divide  S_{x,s}(s)e^{\alpha s} by  S_x^{-}(s) and write out the result as a partial fraction expansion.
  3. Select only those terms in this expansion having poles in the LHP. Call these terms  H(s).
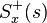  4. Divide  H(s) by  S_x^{+}(s). The result is the desired filter transfer function  G(s).

 

原始文件，环境噪音已经很弱了

 

逐帧实时维纳滤波后

 

posted @ 2015-11-25 23:25  WELEN  阅读(1866)  评论(0)  编辑  收藏  举报