| 这个作业属于哪个班级 | 数据结构-网络20 |
| ---- | ---- | ---- |
| 这个作业的地址 | DS博客作业03--树 |
| 这个作业的目标 | 学习树结构设计及运算操作 |
| 姓名 | 余智康 |
目录
0. 展示PTA总分
1. 本章学习总结
2. PTA实验作业
3. 阅读代码
0.PTA得分截图
1.本周学习总结
1.1 二叉树结构
1.1.1 二叉树的2种存储结构
-
-
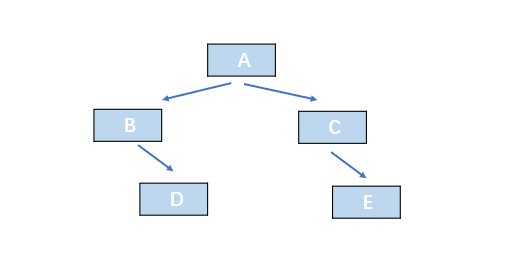
二叉树的顺序存储结构:
-
顺序存储二叉树的图示:

- 顺序存储二叉树树的结构体:
typedef ElemType SqBinTree[MaxSize];
-
顺序存储二叉树的优缺点:
- 优点:
(1)已知某个结点的位置,能快速找到该结点的 双亲 和 孩子 结点。时间复杂度 O(1) - 缺点:
(1)需要将二叉树补成完全二叉树,若是原本的树比较稀疏,会浪费较多的存储空间
(2)若是二叉树树结点数过多,超过了一开始分配的空间,会数组溢出
- 优点:
-
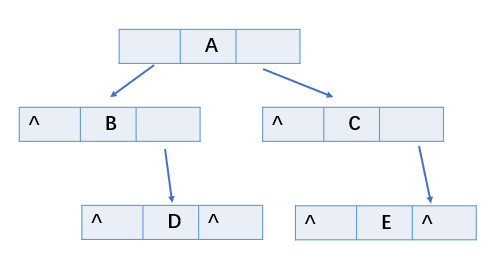
链式存储二叉树结构:
-
链式存储二叉树的图示:
-
链式存储二叉树的结构体:
typedef struct node
{
ElemType data; //数据元素
struct node *lchild; //左孩子
struct node *rchild; //右孩子
}BTNode;
- 链式存储二叉树的优缺点:
- 优点:
(1)节省空间 - 缺点:
(1)查找双亲较麻烦。若是要查找一个二叉树结点的双亲,需要从头遍历二叉树
- 优点:
1.1.2 二叉树的构造
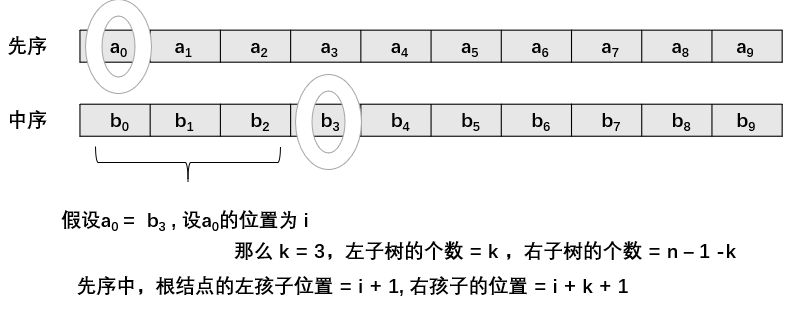
- 先序遍历序列和中序遍历序列构造树:
- 函数接口:
BTree CreateBT(char *pre, char *in, int n); //pre为先序字符串, in为中序字符串, n为结点数
- 思路:
- (1) 创建根结点
- (2)在中序序列中寻找位置
- (3)计算左子树结点个数 k, 右子树结点个数 n-1 -k
- (4)递归调用构建左右子树, 左右子树的 pre 相差k,in 相差k+1

- 代码:
BTree CreateBT(char *pre, char *in, int n)
{
char* p;
int k;
if(n <= 0) return NULL; // 递归出口
BTree BT = new node; //创建根结点
BT -> data = *pre;
for(p = in; p < in+n; p++)
if(*p == *pre) break; //找到时,跳出循环
k = p - in;
CreateBT(pre+1, in, k); //创建左子树
CreateBT(pre+k+1, in+k+1, n-1-k); //创建右子树
}
- 后序遍历序列和中序遍历序列构造树:
- 与先序遍历序列和中序遍历序列构造树类似
- 伪代码
BTree CreateBT(char *post, char *in, int n)
{
递归出口 if n <= 0 do
return NULL
end if
创建根节点BT, BT->data = *(pre+n-1)
在中序中找位置 ,并将 p指针移动到该位置
计算左子树结点个数 k = p-in
构造左子树 BT->lchild = CreateBT(post, in, k)
构造右子树 BT->rchild = CreateBT(post+k, in+k+1, n-1-k)
return BT
}
1.1.3 二叉树的遍历
- 先序遍历:
- (1)访问根节点
- (2)访问左子树
- (3)访问右子树
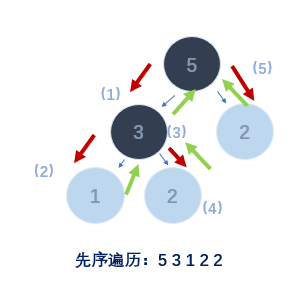
void PreOrder(BTree bt)
{
if(bt == NULL) return; //递归出口
cout << bt->data; //根节点
PreOrder(bt->lchild);
PreOrder(bt->rchild);
}
- 中序遍历:
- 1)访问左子树
- 2)访问根节点
- 3)访问右子树

void InOrder(BTree bt)
{
if(bt == NULL) return;
InOrder(bt->lchild);
cout << bt->data; //根节点
InOrder(bt->rchild);
}
- 后序遍历:
- 1)访问左子树
- 2)访问右子树
- 3)访问根节点
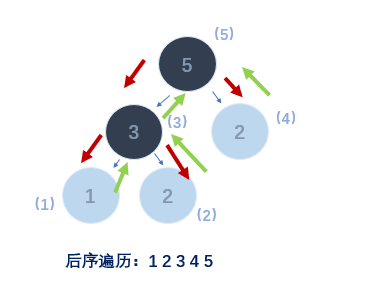
void PostOrder(BTree bt)
{
if(bt == NULL) return;
PostOrder(bt->lchild);
PostOrder(bt->rchild);
cout << bt->data; //根节点
}
- 层次遍历:
- 1)队列
- 2)先将T,入队列
- 3)while循环,队列不空为约束条件
- (4)若队头元素有 左(右)孩子,左(右)孩子入队列
- (5)队头元素出队
初始化队列 que
que.push(T),先将 T入队
while( 队列不空 ) do
q = que.front()
出队,que.pop()
if q 有左孩子,左孩子入队
if q 有右孩子,右孩子入队
end while
1.1.4 线索二叉树
-
线索二叉树的设计:
- 利用空指针域,指向直接前驱,直接后继
- 在结构体中新增两项,LTag、RTag 用于判断记录是否有左、右孩子

-
中序线索二叉树特点:
- 若树结点无左(右)孩子,lchild 指向在中序序列中该结点的直接前驱(后继)
- 为了避免悬空态,增设一个头结点 T

-
中序线索二叉树的查找前驱和后继:
-
1)前驱:
- (1)若有左孩子,则左子树中 最右 的那个结点为前驱
- (2)若无,则前驱线索指针所指的为前驱
-
2)后继:
- (1)若有右孩子,则右子树中 最左 的那个结点为后继
- (2)若无,则后继线索指针所指的为后继
1.1.5 二叉树的应用--表达式树
- 构造表达式二叉树:
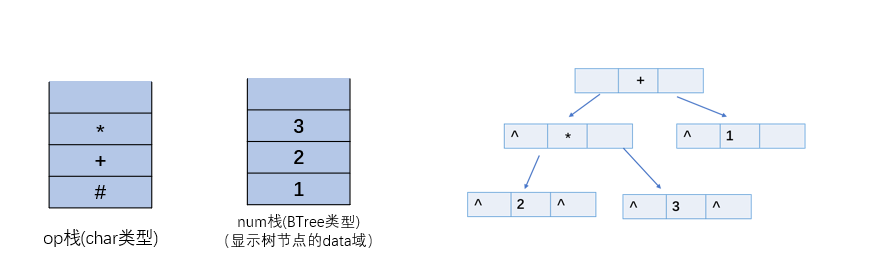
for i=0 to str.size() do
if str[i]不为运算符 do
新建结点 node
调用CreateExpTree()函数,建简单二叉树node,data域为str[i]
num.push(str[i])
end if
else
if op栈为空(op.top()=='#')或 str[i]==1 或 str[i]的优先级高于栈顶运算符
入op栈
end if
else if str[i] == ')'
while(op.top() != '(')
出栈,建树,
end while
将'('出栈
end else if
else if str[i]的优先级低于栈顶运算符
出栈,建树
end else if
end else
end for
while op栈不为空 do
出栈,建树
end while
T = num.top();
- 表达式二叉树的计算
//层次遍历将树节点存入op_num栈中,然后根据计算后缀表达式的方法计算
将根结点压入栈,temp.push(T)
while temp栈不为空 do
取出栈顶,放在 bt 中
出栈
op_num.push(bt->data),将bt所指的数据压入op_num栈
如果bt存在左孩子,左孩子入栈
如果bt存在右孩子,右孩子入栈
end while
while op_num栈不为空 do
op = op_num.top()
if op 不为运算符
(op-'0')入caculate栈(double类型)
op_num栈 出栈
end if
else
num2 = caculate.top(), 出栈
num1 = caculate.top(), 出栈
计算 num1 op num2, 结果放在result中
result 入caculate栈
op_num栈 出栈
end else
end while
1.2 多叉树结构
1.2.1 多叉树结构
主要介绍孩子兄弟链结构
-
孩子兄弟链图示:
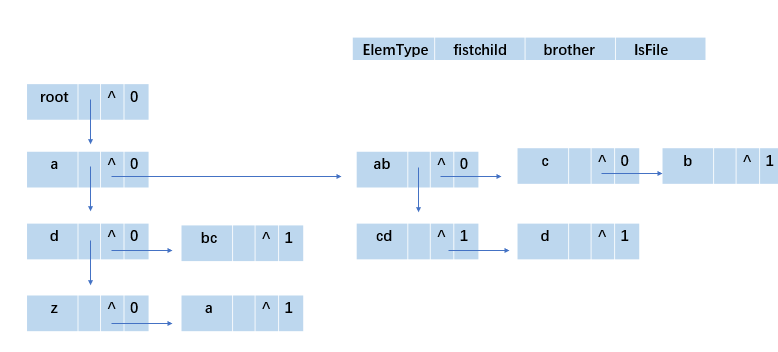
-
孩子兄弟链结构体:
typedef struct tnode
{
ElemType data; //数据域
struct tnode * fistChild; //长子
struct tnode * brother; //兄弟结点
}TSBNode, * TSB; // Tree Son Brother
1.2.2 多叉树遍历
- 先序遍历:
- 1) 访问根节点
- 2) 按照从左往右的顺序先序遍历根节点的每一棵子树
- 如图如图
- 红、绿线为经历结点的顺序,蓝线为树结构
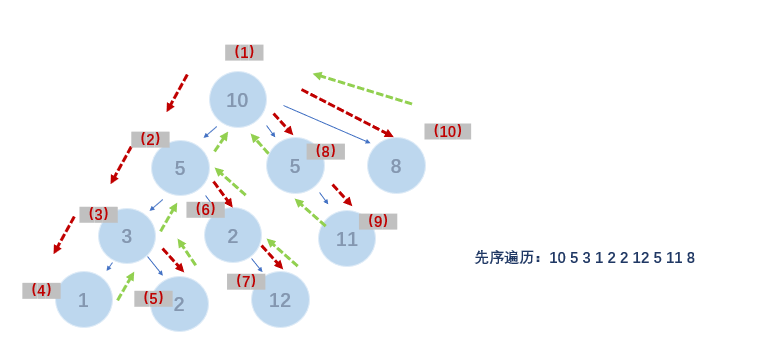
- 红、绿线为经历结点的顺序,蓝线为树结构
1.3 哈夫曼树
1.3.1 哈夫曼树定义
-
哈夫曼树是什么: 在 n 个带权叶子结点构成的所有二叉树中,带权路径 WPL(叶子权值 × 路径长度) 最小的二叉树被称为哈夫曼树,或是最优二叉树
-
哈夫曼树的作用: 如哈夫曼编码,使用频率越高的字符采用越短的编码
1.3.2 哈夫曼树的结构体
教材是顺序存储结构,也可以自己搜索资料研究哈夫曼的链式结构设计方式。
- 顺序存储哈夫曼树:
typedef struct
{
int data; //结点值
double weight; //权值
int parent; //双亲结点
int lchild; //左孩子结点
int rchild; //右孩子结点
}HTNode;
- 链式存储哈夫曼树:
typedef struct HTNode {
char data;
double weight;
int deep;
struct HTNode* lnode;
struct HTNode* rnode;
struct HTNode* parent;
}HTNode, * HTree;
1.3.3 哈夫曼树构建及哈夫曼编码
结合一组叶子节点的数据,介绍如何构造哈夫曼树及哈夫曼编码。
(可选)哈夫曼树代码设计,也可以参考链式设计方法。
- 构建哈夫曼树:

-
哈夫曼树代码设计(顺序):
-
1)初始化哈夫曼数组,n个叶子结点, 2n-1个总结点
- (1)所以树节点(2n-1个)的parent、lchild、rchild 赋值为 -1
- (2)输入n个叶子结点的 data 和 weight 值 (存放在ht[0] ~ ht[n-1])
-
2)构造非叶子结点 ht[i] (存放在ht[n] ~ ht[2n-2]) (for i=n to 2n-2 )
- (1)在 ht[0] ~ ht[n-1]中的根节点中(即parent为-1),找出最小和次小的两个结点 ht[lnode] 和 ht[rnode]
- (2)将 ht[lnode] 和 ht[rnode] 的 parent 赋值为 i
- (3)ht[i].weight = ht[lnode].weight + ht[rnode].weight
-
伪代码:
void CreateHT(HTNode ht[], int n)
{
for i = 0 to 2n-2 //所有结点初始化
将 ht[i]的 parent、lchild、rchild 置为-1
end for
for i = 0 to n-1
输入叶子结点的 data 和 weight
end for
for i = n to 2n-2
min1 = min2 = 99999; lnode = rnode = -1 ,重置min1、min2、lnode、rnode
for k=0 to i-1
找最小、次小,并将所处位置记录在lnode、rnode中
end for
将 ht[lnode] 和 ht[rnode] 的 parent = i
ht[i].weight = ht[rnode].weight + ht[lnode].weight
将 ht[i] 的左右孩子记为 ht[lnode]、ht[rnode]
end for
}
-
哈夫曼树代码设计(链式):
-
1) 初始化哈夫曼树
- (1) 先创建 n 个二叉树(仅有根节点),根节点存放在 ht[]数组中
- (2) 将 n 个根节点的 parent、lnode、rnode 指针指向 NULL
- (3) 将 n 个叶子结点的权值,放入 ht[i].weight 中
-
2) 合并、删除,构建哈夫曼树
- (1)定义 count = n(一开始输入的叶子结点数),外循环 while(count != 1),每次合并根节点时,ht[]中减少两个,增加一个,即减少一个,则count--
( )故当最后哈夫曼树建成时,count == 1 - (2)在while循环中,先重置londe = rnode = -1,并将最小和次最小赋值为一个大值(如1.79769e+308);
( ) ①在根节点中寻找权值的最小,和次小值,记录下标在 lnode 和 rnode中,
( )找到最小和次最小后,②合并最小和次最小根结点的树,生成新的根结点,放入ht[lnode]中,并将ht[rnode] = NULL
(备注)①:根节点判断:先进行 if判断ht[i]是否为空。若不为空,判断 ht[i].parent 是否为空,
(备注)②:新的根结点的左右孩子分别指向 ht[lnode]、ht[rnode],新的根结点的 parent = NULL;并将ht[rnode]、ht[lnode]的双亲结点修改为新的根结点 - (3)while循环结束后,在ht[]中找到不为空的 ht[i], 返回 ht[i],ht[i] 即为完成后的哈夫曼树根节点
- (1)定义 count = n(一开始输入的叶子结点数),外循环 while(count != 1),每次合并根节点时,ht[]中减少两个,增加一个,即减少一个,则count--
-
建哈夫曼树代码:
HTree CreateHT(HTree ht[], int n)
{
int count = n;
int i;
double min1, min2; // min1 最小, min2次最小
int lnode, rnode;
while (count != 1)
{
min1 = min2 = 1.79769e+308;
lnode = rnode = -1;
for (i = 0; i < n; i++)
{
if (ht[i] != NULL)
{
if (ht[i]->parent == NULL)
{
if (ht[i]->weight < min1)
{
min2 = min1;
min1 = ht[i]->weight;
rnode = lnode;
lnode = i;
}
else if (ht[i]->weight < min2)
{
min2 = ht[i]->weight;
rnode = i;
}
}
}
}
if (lnode != -1 && rnode != -1)
{
HTree pnode = MergeTree(ht[lnode], ht[rnode]);
ht[lnode] = pnode;
ht[rnode] = NULL;
count--;
}
}
for (int i = 0; i < n; i++)
{
if (ht[i] != NULL)
return ht[i];
}
}
- 合并树的代码:
HTree MergeTree(HTree htLeft, HTree htRight)
{
HTree ht = new HTNode;
ht->weight = htLeft->weight + htRight->weight;
ht->lnode = htLeft;
ht->rnode = htRight;
ht->parent = NULL;
htLeft->parent = htRight->parent = ht;
return ht;
}
1.4 并查集
-
并查集是什么:
- 并查集是查找一个运算的所属集合,合并2个元素各自的专属集合
-
并查集的作用:
- 用于朋友圈、亲戚关系一类问题
-
并查集的优势:
- 元素的关系易查找,要查找元素的关系是否处于同一集合,只需要访问找到它们的根节点,判断根节点是否相等
- 集合合并较方便,只需要判断两个集合的Rank,并对根节点进行合并操作
-
并查集的结构体:
typedef struct node
{
int data;
int rank;
int parent;
}UFSTree;
- 并查集的查找与合并
- 并查集的查找:
int FindSet(UFSTree t[], int x)
{
if (x != t[x].parent)
return FindSet(t, t[x].parent);
else
return x;
}
- 并查集的合并:
void Union(UFSTree t[], int x, int y)
{
x = FindSet(t, x);
y = FindSet(t, y);
if (t[x].rank > t[y].rank)
t[y].parent = x;
else
{
t[x].parent = y;
if (t[x].rank == t[y].rank)
t[y].rank++;
}
}
1.5 树的认识及学习体会(
- 树的认识及体会:
- 在对树的操作中,经常涉及到递归
- 因为平时对递归几乎没有去使用,所以开始的时候对于树的建树、遍历、求高度、查找等等都对递归有使用的情况下,有些怕吧,感觉记不住,搞不来。
之后学下来,代码敲下去,博客补充完。慢慢地感觉还行,对树、对递归也能理解了,也不至于看着树的问题而一脸懵逼了。 - 码树的代码的时候,出现异常的话,查错比较麻烦。
2.PTA实验作业
此处请放置下面2题代码所在码云地址(markdown插入代码所在的链接)。如何上传VS代码到码云
- 二叉树叶子结点带权路径长度和:https://gitee.com/welcome_to_tommrow/pta-code/blob/master/二叉树叶子结点带权路径长度和.cpp
- 目录树:https://gitee.com/welcome_to_tommrow/pta-code/blob/master/7-7 目录树 .cpp
2.1 二叉树叶子结点带权路径长度和

2.1.1 解题思路及伪代码
-
1)思路:
- (1)将顺序二叉树,使用递归转换为链式存储的二叉树 BinTree CreateBtree(string str,int i)
- (2)叶子结点的 WPL = 权重 × 路径长度 void CalculateWPL(BinTree BT, int h, int& WPL)
( )① 判断叶子结点(左右孩子为空); ② 路径长度,引入形参 h; ③ 叶子 WPL,引用型形参 WPL
-
2)伪代码:
void CalculateWPL(BinTree BT, int h, int& WPL)
{
递归出口,if BT == NULL
if BT为叶子结点 do
计算WPL,WPL += (BT->data - '0') * h
end if
进入左子树,CalculateWPL(BT->lchild, h+1, WPL)
进入右子树,CalculateWPL(BT->rchild, h+1, WPL)
}
2.1.2 总结解题所用的知识点
- (1)顺序存储的二叉树转化为链式存储的二叉树
- (2)字符型的数字转化为整型的数字
- (3)寻找叶子结点
- (4)二叉树结点的路径长度计算
2.2 目录树

2.2.1 解题思路及伪代码
- 树的结构体用孩子兄弟链,还需要另外加上一项ISFile,用来保存是否是文件的信息
- 树的初始化,函数 void InitTSB
- 树的创建,函数 void PushTSB
- 树的打印,函数 void PrintTSB
- 树的初始化: 动态申请,data项清空,长子和兄弟指向NULL
- 树的创建:
- 树创建刚开始的思路: 刚开始的思路及伪代码有些错误,实际编程中有进行修改,思路大体上没毛病
- 1)输入line,有line行,用i计数,小于line循环进行,输入str,将p指向根结点
- 2)针对每一行,需要切分,用j计数,小于str.size()循环进行。当遇到'\'或是' '表示结束,遇到'\'将flag = 0,遇到' '将flag = 1,跳出
- 3)初始化结点node,将flag放入到 node->IsFile 中,在将切分好的字符串放入 node->data 中
- 4)将node插入树中,分为两大种情况,一是前一个结点的长子为空:直接修改长子关系;而是前一个结点的长子不为空:查找是否存在该结点,若不存在则插入
- 5)处理完节点后,要将 指针p 移动到该结点位置
- 2.1)字符串处理:
用j、k计数。for循环,k++,当str[k]为 '\',或是' '时,跳出循环。
执行另一个for循环,for j to j = k-1,dataStr += str[j],将字符串切分好放入dataStr中
// 下面这个最开始的伪代码有明显错误,后面实际编程中加以修改了,但大体思路是这样的
while(j<str.size())
if (str[k] == '\\' || str[k] ==' ')
{
if '\\' flag = 0
if ' ' flag = 1
break;
}
for j to k-1
dataStr += str[z]
end for
j++
end while
- 4.1) 树结点的插入:
- 对于排序:需要考虑是否为文件,文件位于目录后
- 对于插入:先考虑长子与该结点的关系,判断是否需要修改长子。若不需要修改长子,使用线性表插入的知识,进行树结点的插入
TSB InsertTSB(TSB& BT, TSB &node)
{
p = BT
if (p->data > node ->data 且 p 与 node为同类型)或者 (p为文件,node为目录)
将node->brother = p
返回 空,从而在主调函数中修改长子关系
end if
while(p->brother != NULL) do
找前驱
end while
将node插入
}
- 树创建刚开始的伪代码:
cin >> line
for i = 0 to i = line-1 do
cin >> str
p = BT
for j = 0 to j = str.size() - 1 do
处理str字符串,将切割后的str放到str_data; 判断是否文件,放入flag
新建结点TSB,
初始化TSB, TSB-> data = str_data; TSB ->IsFile = flag
if (p -> fistchild == NULL)
p -> fistrchild = TSB
p = TSB
end if
if( p-> fistchild != NULL)
在fistchild的兄弟链中寻找TSB->data
if 找得到
p = 该兄弟结点
end if
if 找不到
将TSB插入兄弟链中
end if
end if
end for
end for
-
后来对树创建的修改:
-
(1)对于一开始的思路,后来发觉可以直接对树结点的 data 和 IsFile 进行操作,故不再另外定义遍历 str_data,j,和flag
-
(2)对于步骤 2)从开始的在循环内遇到 '\'或' '进行对 IsFile 赋值再跳出
....改为 ---> 在循环内将 IsFile 反复置为 1。若是遇到'\',则置为 0后,将计数的k++,然后跳出循环。
....由于' '只会出现在末尾,则由计数 k达到限制退出的说明为文件,由于break退出的说明为目录 -
(3)对于原本字符串处理的循环,因为break跳出循环,极可能导致字符串str未读取完,故在原本的 while 循环外在嵌套了一个while循环,确保字符串读取完毕
-
-
树的打印,以及修改后的树的创建伪代码:
void PrintTSB(TSB BT,int h) // 树的打印
{
递归出口,BT == NULL
for i = 0 to h-1 //(格式控制)
输出' '
end for
输出 BT -> data, 并换行
进入长子 PrintTSB(BT->fistChild, h + 1)
进入兄弟 PrintTSB(BT->brother, h)
}
void PushTSB(TSB& BT) //修改后的树的创建伪代码
{
输入line
for i = 0 to line - 1
输入字符串str,如"ab\cd"
k = 0, p = BT,将 k,p 重置
while str未遍历完(k < str.size()) do
新建树结点 node, InitTSB(node)
while str未遍历完(k < str.size()) do //该循环用于分割字符串,建树结点
将 node -> IsFile 置为 1, 当因为 k>=str.size()结束循环时,说明该结点是文件
if 该结点是目录,即 str[k] == '\\'时 do
将 node -> IsFile 置为0, 该结点为目录
k递增
break跳出循环
end if
node->data += str[k++],利用C++ string数据类型的特点,填入data
end while
end while
end for
}
2.2.2 总结解题所用的知识点
- 1)创建孩子兄弟树
- (1)拆分字符串
- (2)孩子兄弟树的插入:① 长子为空;② 需要修改长子关系;③ 普通线性表插入
- 2)打印孩子兄弟树
- (1)结合树的高度进行格式控制
3.阅读代码
3.1 对称二叉树
- 题目: 给定一个二叉树,检查它是否是镜像对称的。

- 代码:
class Solution {
public:
bool check(TreeNode *p, TreeNode *q) {
if (!p && !q) return true;
if (!p || !q) return false;
return p->val == q->val && check(p->left, q->right) && check(p->right, q->left);
}
bool isSymmetric(TreeNode* root) {
return check(root, root);
}
};
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/symmetric-tree/solution/dui-cheng-er-cha-shu-by-leetcode-solution/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
3.2 该题的设计思路及伪代码
-
思路:
- (1)树互为镜像 即每棵树的 右子树 和 另一棵树的右子树相等
- (2)两个指针,一个移动向右子树,另一个指针移向左子树,判断结点值是否相等,是否镜像对称
-
伪代码:
bool check(TreeNode *p, TreeNode *q)
{
递归出口1:if q 和 p 都为空 do
返回 true
end if
递归出口2:if q 或 p 有一个为空 do
返回 false
end if
判断 p,q 所指树节点的数据域是否相等 && 递归 p左孩子,q右孩子 && 递归 p右孩子,q左孩子
即 return p->val == q->val && check(p->left, q->right) && check(p->right, q->left);
}
3.3 分析该题目解题优势及难点。
-
1)题解优势:
- (1)使用两个指针同步移动
- (2)代码通俗易懂
-
2)难点:
- (1)分析满足镜像树的条件
- (2)两个指针同步移动
- (3)最后的 return 很厉害,在看题解前完全没想到这样子做
return p->val == q->val && check(p->left, q->right) && check(p->right, q->left);




