本来想着一天速通字符串，看来我还是想多了。

长文警告，本文目前有大约 0.9W 个字，可以当小说看

可能需要的前置

  • 字符串哈希

  • KMP

  • trie 树

  • manacher 算法

可能涵盖的内容

目前已有的：

  • 后缀数组 SA
  • AC 自动机
  • 后缀自动机

未来可能会有的：

  • 扩展 KMP

  • 回文自动机

  • 子序列自动机

本文可能会有很多错误，还请发现的大佬们指出，本蒟蒻感到非常荣幸。

参考资料

  • 后缀数组

xMinh大佬 的 讲解

Rainy7大佬 的 学习笔记

曲神学长 的 算法总结

Ckj 同机房大佬 的 学习笔记

  • AC 自动机

Hastieyua 大佬 的 详细讲解

  • 后缀自动机

OI Wiki

对此，本蒟蒻不胜感激

如有侵权问题，请联系我，我会马上标明出处或修改。

声明

本文中 \(|u|\) 表示字符串 \(u\) 的长度，\(\Sigma\) 表示字符集，\(|\Sigma|\) 表示字符集大小。

更新日志

2022.03.15 完成后缀数组和 AC 自动机的更新

2022.03.16 完成后缀自动机的更新

2022.03.17 修改了几处公式错误

后缀数组

后缀排序

模板题：P3809 【模板】后缀排序

后缀数组可以用来实现一个字符串的每个后缀按照字典序排序的操作，根据这个操作，可以引申出很多用法。

后缀数组 SA 的实现是基于基数排序的思想，在普通基数排序的基础上加了倍增。

算法流程大致如下：

这里假设待排序字符串是 abacabc。

  • 首先用一个字母进行排序，结果更新到一个 rk 数组（表示该后缀排名），上述字符串应为 1 2 1 3 1 2 3。

  • 然后相邻两个字符串拼接起来，对于每个后缀，得到它长度为 \(2\) 的前缀的两位标号。对于最后一个长度为 \(1\) 的后缀，因为没有第二位字符串，所以它第二位字典序最小，通过补零解决。此时上述字符串的标号为 12 23 13 31 12 23 30。

  • 然后对这些原来相同的后缀们重新排序，标号变成 1 3 2 5 1 3 4。

  • 然后我们重复第二步过程，让每个后缀和它隔一个的那个后缀拼接起来，得到它长度为 \(4\) 的前缀的两位标号。同理，不够的补零。此时上述字符串标号为 12 35 21 53 14 30 40，注意要隔一个，因为现在每一位代表的是两个字符的字符串的排序。

  • 然后重新排序，得到 1 5 3 7 2 4 6。

  • 我们发现现在标号已经没有重复了的，得到的数字即是对应后缀在所有后缀中的排名。

我们发现这样子每次每个后缀的长度会 \(\times2\)，所以最多只会进行 \(O(\log n)\) 次拼接-标号过程，每次都是 \(O(n)\) 时间，总时间复杂度 \(O(n\log n)\)。

其实后缀数组还有另外一个算法 DC3，能做到时间复杂度 \(O(n)\)，可是由于本蒟蒻不会 代码复杂度过高，而且空间复杂度不优，我们还是常用 SA。

为了方便后面的使用，这里封装成了结构体。

#include<bits/stdc++.h>
using namespace std;
const int N=1e6+10;
int n;
char s[N];
struct SA{
	int m=131,x[N],y[N],c[N],sa[N],nx[N],hei[N];
	void get_sa(){
		for(int i=1;i<=n;i++)c[x[i]=s[i]]++;//处理第一个字符的排序 
		int l=0;
		for(int i=1;i<=m;i++)c[i]+=c[i-1];
		for(int i=n;i>=1;i--)sa[c[s[i]]--]=i;
		for(int k=1;k<=n;k<<=1){
			int num=0;
			for(int i=n-k+1;i<=n;i++)y[++num]=i;//后面的字符串已经排好序了，不需要加入排序 
			for(int i=1;i<=n;i++)if(sa[i]>k)y[++num]=sa[i]-k;
			for(int i=1;i<=m;i++)c[i]=0;//桶排 
			for(int i=1;i<=n;i++)c[x[i]]++;
			for(int i=2;i<=m;i++)c[i]+=c[i-1];
			for(int i=n;i>=1;i--)sa[c[x[y[i]]]--]=y[i],y[i]=0;//倒序附排名，保证排序稳定 
			swap(x,y);
			num=1,x[sa[1]]=1;
			for(int i=2;i<=n;i++){//处理下一次排序的关键字 
				if(y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k])x[sa[i]]=num;//若两个都相等，那么当前两个后缀是相同的 
				else x[sa[i]]=++num; 
			}
			if(num==n)break;//如果已经排完了，就不管了 
			m=num;
		}
	}
}sa;
signed main(){
	scanf("%s",s+1),n=strlen(s+1);
	sa.get_sa();
	for(int i=1;i<=n;i++)printf("%d ",sa.sa[i]);
	puts("");
}

注意，在上述代码中，sa 数组存的是排名为 \(i\) 的后缀的第一个字符在原串中的位置，不要搞混了。如果要求 第 \(i\) 个后缀的排名，也就是上述解释中的标号，需要再进行转化。因为 \(sa\) 和 \(rk\) 是互逆的，也就是 \(sa_{rk_i}=i\)，所以这个过程比较简单，便不再赘述。

评测记录

当然，这只是万里长征路中的微不足道的一步，但同时也是意义非凡的一步。

后缀数组的运用：height 数组与 LCP

先摆出一些定义：

\(rk_i\) 表示第 \(i\) 个后缀的排名。

\(lcp(s,t)\) 表示两个字符串 \(s\) 和 \(t\) 它们的最长公共前缀，在本文中，表示编号分别为 \(s,t\) 的两个后缀的最长公共前缀。

\(hei_i=lcp(sa_i,sa_{i-1})\)，也就是排名为 \(i\) 和 \(i-1\) 的两个后缀的最长公共前缀。

\(h_i=hei_{rk_i}\)，也就是当前后缀与比他排名前一位的后缀最长公共前缀。

接下来，是一些性质。

性质 1：\(lcp(i,j)=lcp(j,i)\)。

并不需要什么证明。

性质 2：\(lcp(i,i)=n-sa_i+1\)。

可以发现，两个完全一样的字符串它们的最长公共前缀就是它本身，长度为 \(n-sa_i+1\)。

性质 3 LCP Lemma：\(lcp(i,j)=\min(lcp(i,k),lcp(k,j))(1\le i\le k\le j \le n)\)。

这里开始有点烧脑了。

设 \(p=\min(lcp(i,k),lcp(k,j))\)，则有 \(lcp(i,k)\ge p,lcp(k,j)\ge p\)。

设 \(sa_i,sa_j,sa_k\) 所代表的后缀分别是 \(u,v,w\)。

得到 \(u,w\) 前 \(p\) 个字符相等，\(w,v\) 前 \(p\) 个字符也相等，

所以得到 \(u,v\) 前 \(p\) 个字符也相等，

设 \(lcp(i,j)=q\)，则有 \(q\ge p\)。

接下来，我们采用反证法证明 \(q=p\)。

假设 \(q>p\)，即 \(q\ge p+1\)。

因此 \(u_{p+1}=v_{p+1}\)。

因为 \(p=\min(lcp(i,k),lcp(k,j))\)，所以有 \(u_{p+1}\not=w_{p+1}\) 或 \(v_{p+1}\not=w_{p+1}\)。

所以得到 \(u_{p+1}\not=v_{p+1}\)，与前面矛盾。

因此得到 \(q\le p\)，综合得 \(q=p\)，即 \(lcp(i,j)=\min(lcp(i,k),lcp(k,j))(1\le i\le k \le j \le n)\)。

性质 4 LCP Theorem：\(lcp(i,j)=\min(lcp(k,k-1))(1<i\le k\le j\le n)\)。

我们可以用刚得到的性质三来证。

\(lcp(i,j)=\min(lcp(i,i+1),lcp(i+1,j))\\=\min(lcp(i,i+1),\min(lcp(i+1,i+2),lcp(i+2,j))\\=\dots=min(lcp(k,k-1))(i\le k\le j)\)

性质 5：\(h_i\ge h_{i-1}-1\)。

以下证明转载至简书-信息学小屋：

回归正题，设 \(hei_1=0\)，考虑如何求 \(hei\)。

因为 \(lcp(i,j)=min(lcp(k,k-1))(1<i\le k\le j\le n)\)，

所以 \(lcp(i,j)=min(hei_k)(i<k\le j)\)，

前面有提过 \(sa_{rk_i}=i\)，所以 \(hei_{i}=h_{sa_i}\)。

我们先把 \(h\) 求出来，然后就能利用性质 4，用 rmq 之类的东西求一下，能做到 \(O(1)\) 查询。

int n,lg[N];
char s[N];
struct SA{
	int m=131,x[N],y[N],c[N],sa[N],rk[N],nx[N],hei[N],h[N];
	int mn[N][20];
	void get_sa(){
		for(int i=1;i<=n;i++)c[x[i]=s[i]]++;//处理第一个字符的排序 
		int l=0;
		for(int i=1;i<=m;i++)c[i]+=c[i-1];
		for(int i=n;i>=1;i--)sa[c[s[i]]--]=i;
		for(int k=1;k<=n;k<<=1){
			int num=0;
			for(int i=n-k+1;i<=n;i++)y[++num]=i;//后面的字符串已经排好序了，不需要加入排序 
			for(int i=1;i<=n;i++)if(sa[i]>k)y[++num]=sa[i]-k;
			for(int i=1;i<=m;i++)c[i]=0;//桶排 
			for(int i=1;i<=n;i++)c[x[i]]++;
			for(int i=2;i<=m;i++)c[i]+=c[i-1];
			for(int i=n;i>=1;i--)sa[c[x[y[i]]]--]=y[i],y[i]=0;//倒序附排名，保证排序稳定 
			swap(x,y);
			num=1,x[sa[1]]=1;
			for(int i=2;i<=n;i++){//处理下一次排序的关键字 
				if(y[sa[i]]==y[sa[i-1]]&&y[sa[i]+k]==y[sa[i-1]+k])x[sa[i]]=num;//若两个都相等，那么当前两个后缀是相同的 
				else x[sa[i]]=++num; 
			}
			if(num==n)break;//如果已经排完了，就不管了 
			m=num;
		}
		for(int i=1;i<=n;i++)rk[sa[i]]=i;
	}
	void get_h(){
		for(int i=1,k=0;i<=n;i++){
			int j=sa[rk[i]-1];k-=(k!=0);
			while(s[i+k]==s[j+k])++k;
			h[i]=hei[rk[i]]=k;
		}
	}
	void rmq(){
		for(int i=2;i<=n;i++)lg[i]=lg[i>>1]+1;
		for(int i=1;i<=n;i++){
			mn[i][0]=hei[i];
			for(int j=1;i>=(1<<j);j++)mn[i][j]=min(mn[i][j-1],mn[i-(1<<j-1)][j-1]);
		}
	}
	int lcp(int l,int r){
		if(l>r)swap(l,r);++l;
		int d=lg[r-l+1];
		return min(mn[r][d],mn[l+(1<<d)-1][d]);
	}
}sa;

后缀数组的简单运用

例 1：P2408 不同子串个数

题目大意：统计一个字符串中本质不同的子串个数。

ps：本题可以用后缀自动机做，但同时也是后缀数组好题。

正难则反，我们考虑计算所有子串个数减去相同子串个数。

我们求出 \(hei\) 之后，剪掉相同前缀数量即可。

由于篇幅问题，本文中例题只放主要代码。

signed main(){
	scanf("%lld%s",&n,s+1);
	sa.get_sa(),sa.get_h();
	int ans=n*(n+1)/2;
	for(int i=1;i<=n;i++)ans-=sa.hei[i];
	printf("%lld\n",ans);
}

评测记录

例 2：P3763 [TJOI2017]DNA

题目大意：给出两个串 \(S_0\) 和 \(S\)，求 \(S_0\) 中有多少个长度和 \(S\) 相同的子串，使得这个子串能通过修改 \(\le 3\) 个字符与 \(S\) 相同。多组询问。

ps：本题似乎有多项式做法，有兴趣的可以了解一下。

我们可以把 \(S\) 插入到 \(S_0\) 后面，中间用一个精心挑选的分隔符，然后就可以得到 \(S_0\) 的每个后缀和 \(S\) 的 lcp 了。

然后枚举每一个开头，和 \(S\) 的 lcp 暴力往后跳，跳到一个不匹配的位置就跳过，只要跳完后失配点不超过三个 就能统计。处理以每个字符开头的子串时间复杂度 \(O(1)\)。

因为是多测，注意封装函数时是否清空函数，宁愿多清也不漏清。

int _;
scanf("%d",&_);
for(;_--;){
    scanf("%s%s",s+1,t+1);
    k=n=strlen(s+1),m=strlen(t+1);
    s[++n]='#';
    for(int i=1;i<=m;i++)s[++n]=t[i];
    sa.get_sa(),sa.get_h(),sa.rmq();
    int ans=0;
    for(int i=1;i<=k-m+1;i++){
        int __=0;
        for(int j=1;__<=3&&j<=m;){
            //				printf("%d %d\n",i,j);
            if(s[i+j-1]^s[k+j+1])++j,++__;
            else j+=sa.lcp(sa.rk[i+j-1],sa.rk[k+j+1]);
        }
        if(__<=3)++ans;
    }
    printf("%d\n",ans);
}

下面给出几道题作为练习。

评测记录

P4248 [AHOI2013]差异

P4051 [JSOI2007]字符加密

P1117 [NOI2016] 优秀的拆分

CF1043G Speckled Band

Oiclass 4088 字符串 ps：可以用后缀自动机做，也可以用后缀数组+回滚莫队做。

接下来，后缀数组的事情可能就要告一段落了。

AC 自动机

AC 自动机作为自动机家族里面几乎是最容易入手的一个，这里介绍一下。

这一部分需要读者能够深刻理解 trie，了解 kmp。

从 kmp 到 AC 自动机

我们回忆一下 kmp 是处理什么问题的：单模式串匹配问题。

那如果很多个模式串和一个文本串匹配呢？

这时候，AC 自动机重磅出击！

首先有个很 naive 的想法，把模式串们放进一个 trie 树上，然后枚举每一个文本串的后缀，放上去匹配一下。

举个例子，假设我们有模式串 abc，abb，bcc，文本串 abccabbcc。

那么我们建出来的 trie 树大概就是这样。

这个时候如我们先匹配 a，然后走到 abc，发现匹配不了了，倒回起点，从 b 开始匹配，匹配到 bcc。

思考：如果这样子下去，我们会发现这个思路绝对会 T。

考虑如何优化这个过程。

我们发现，我们从 abc 走到下一个 c 时，没有办法匹配，我们把这个情况叫做失配。但是，如果把开头的 a 扔掉，我们发现我们能够走到 bcc。也就是说，每次失配时，我们可以把一些前缀扔掉，走到另外一个能让它不失配的点，这样次就不需要每次失配都倒回起点重头再来。

如果我们对每个点，向它丢掉最短非空前缀之后的点连一条边，（保证状态尽量长）那么，每次失配了就跳到上一个点上就好了。

练完之后的图大概长这样：

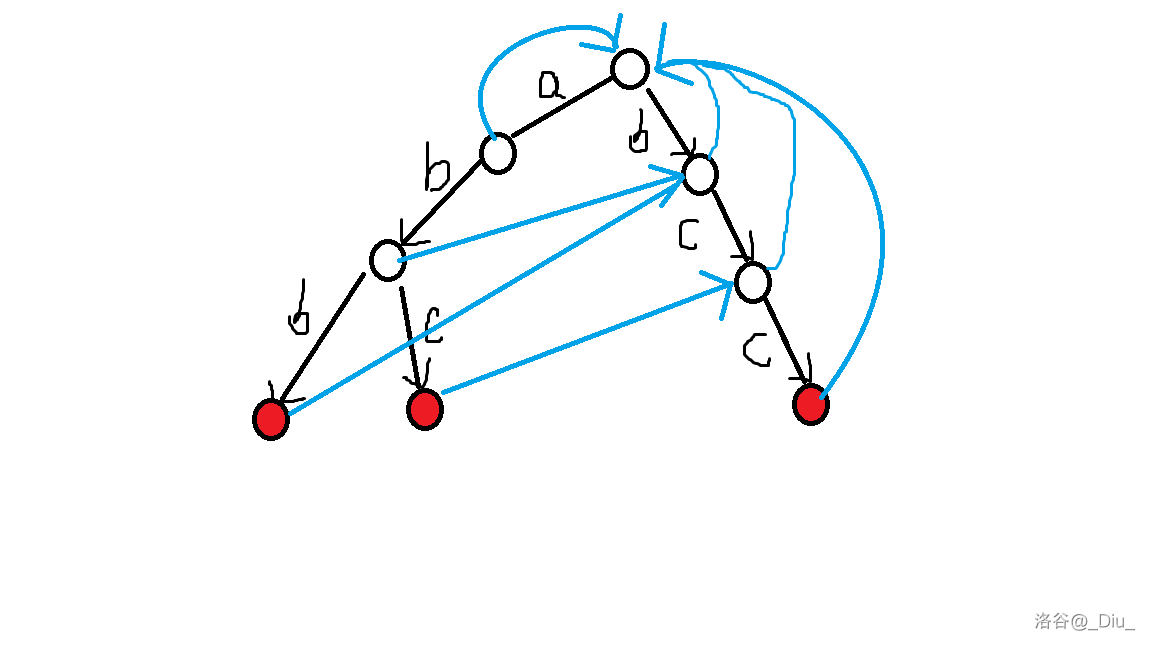
我们把这样练得边叫做 fail 指针。

我们考虑这样匹配：从字典树的根节点开始依次添加匹配串的字符。遇到失配时，顺着 fail 指针找到能匹配新字符的第一个状态。若当前状态 fail 链上的某个祖先是终止状态，则成功匹配模式串 。

考虑如何快速找到失配点，如果有这个儿子，可以把 fail 指针指向父亲的对应 fail 指针，否则把儿子设为父亲的对应 fail 指针，方便之后的更新。这里可以用类似广搜的方法更新，详见代码。

如果我们查询的时候暴力向上跳失配点，直到根节点，统计答案，这样的话时间复杂度最多能被卡到 \(O(模式串长\times 文本串长)\)，能过 P3796 【模板】AC 自动机（加强版），但是过不了 P5357 【模板】AC 自动机（二次加强版）。

这些操作是依据 trie 树的，因此 AC 自动机也被称作 trie 图。

void push(char *s,int k){
	int p=0,len=strlen(s+1);
	for(int i=1;i<=len;i++){
		int c=s[i]-'a';
		if(!tr[p][c])tr[p][c]=++tot;
		p=tr[p][c];
	}
	vis[num[k]=p]=1;
}
void get_fail(){
	queue<int> q;
	for(int i=0;i<26;i++){
		if(tr[0][i])q.push(tr[0][i]);
	}
	while(!q.empty()){
		int p=q.front();q.pop();
		for(int i=0;i<26;i++){//最难理解的部分
			if(tr[p][i])fail[tr[p][i]]=tr[fail[p]][i],q.push(tr[p][i]);
			else tr[p][i]=tr[fail[p]][i];
		}
	}
}
void find(char *s){
	int len=strlen(s+1);
	int p=0;
	for(int i=1;i<=len;i++){
		int c=s[i]-'a';
		p=tr[p][c];
		for(int k=p;k;k=fail[k])ans[k]++;
	}
}

加强版评测记录

我们继续考虑优化这个过程。

我们发现在原来暴力跳的过程中，我们每经过一次 abc，都要统计一次 bc，如果有 c 的话也要跟的统计，非常麻烦，所以我们考虑能不能一次性统计完。比如我们到达一个点打一个标记，打完标记后统一上传，这样就能够优化这个过程了。

那么，我们如何确定上传顺序呢？

拓扑排序！

我们在统计答案的时候打一个标记，然后用类似拓扑排序的方法，从深度大的点更新到深度小的点。

void find(char *s){
	int len=strlen(s+1);
	int p=0;
	for(int i=1;i<=len;i++){
		int c=s[i]-'a';
		ans[p=tr[p][c]]++;
	}
	queue<int> q;
	for(int i=1;i<=tot;i++)if(!d[i])q.push(i);
	while(!q.empty()){
		int u=q.front();q.pop();
		int v=fail[u];
		d[v]--,ans[v]+=ans[u];
		if(!d[v])q.push(v);
	}
}

评测记录

至此，你已能通过谷上三道模板题了。

AC自动机的简单运用

例 1：P3966 [TJOI2013]单词

模板题，不讲（

例 2：P3121 [USACO15FEB]Censoring G

题目大意：给你一个文本串和一堆模式串，在文本串中找到出现位置最靠前的模式串并删掉，重复这个过程，求最后的文本串。

注意有删除操作，所以我们可以把扫到的节点放到一个栈里面，每次匹配到了就倒退回去就好了。

为了方便输出，我用了 deque 实现。

因为不需要在自动机上统计什么答案，所以也不需要拓扑优化。

inline void find(string s){
	deque<cxk> q;
	register int p=0;
	q.push_back({' ',0});
	for(register int i=0;i<s.size();i++){
		register int c=s[i]-'a';
		register int k=trie[p][c];
		if(num[k]){
			for(int j=1;j<num[k];j++)q.pop_back();
			p=q.back().p;
		}else{
			p=trie[p][c];
			q.push_back({s[i],p});
		}
	}
	q.pop_front();
	while(!q.empty()){
		cout<<q.front().ch;
		q.pop_front();
	}
}

评测记录

例 3：P2292 [HNOI2004] L 语言

题目大意：给出若干个模式串，每次询问一个文本串最长的能被模式串们完全匹配的前缀长度。

属于在 AC 自动机上跑简单 dp。

我们考虑到这建 AC 自动机。

设 \(f_i\) 表示前缀 \(i\) 是否完全匹配，枚举每一个前缀，到这从这一位往前找，每次加入一个点，如果适配了就直接弹（因为必须要完全匹配）。

考虑模式串比较小，所以这样做是可行的。

当然正解是在 AC 自动机上状压，具体可见 扶苏大佬 的 题解。

for(int i=1;i<=len;i++){
    f[i]=false;pos=0;
    for(int j=i;j>=1;j--){ 
        if(!trie[pos][t[j]-'a'])break;
        pos=trie[pos][t[j]-'a']; 
        if(vis[pos]){
            f[i]|=f[j-1];
            if(f[i])break;
        }
    }
}

评测记录

接下来是几道练习，可能有点困难。

P5231 [JSOI2012]玄武密码 ps：也能用后缀数组做。

P2414 [NOI2011] 阿狸的打字机

P3763 [TJOI2017]DNA ps：刚刚在后缀数组有，但是也可以在 AC 自动机上 dp。

P3735 [HAOI2017]字符串

Loj 668 yww 与树上的回文串 ps：点分治与 AC 自动机结合。

51nod1600 Simple KMP ps：对 fail 链的深刻理解，与 LCT 结合。

后缀自动机（SAM)

后缀自动机是能解决很多字符串问题的大力数据结构，虽然有很多问题后缀数组也能解决，但是后缀自动机的优势就是思维量一般没有后缀数组那么。虽然理解后缀自动机的思维量就挺大的。

SAM 可以理解成是一个字符串所有子串的状态的压缩。

同时这是一个很多人选择背板子的做法。

从 trie 到 SAM

先看模板题：P3804 【模板】后缀自动机 (SAM)。

我们发现我们首先要得到所有子串。

比如一个字符串 abcaabcbcca。

我们可以对每一个后缀放到一个 trie 里面，这样 trie 上每个节点就对应原串一个本质不同的子串。

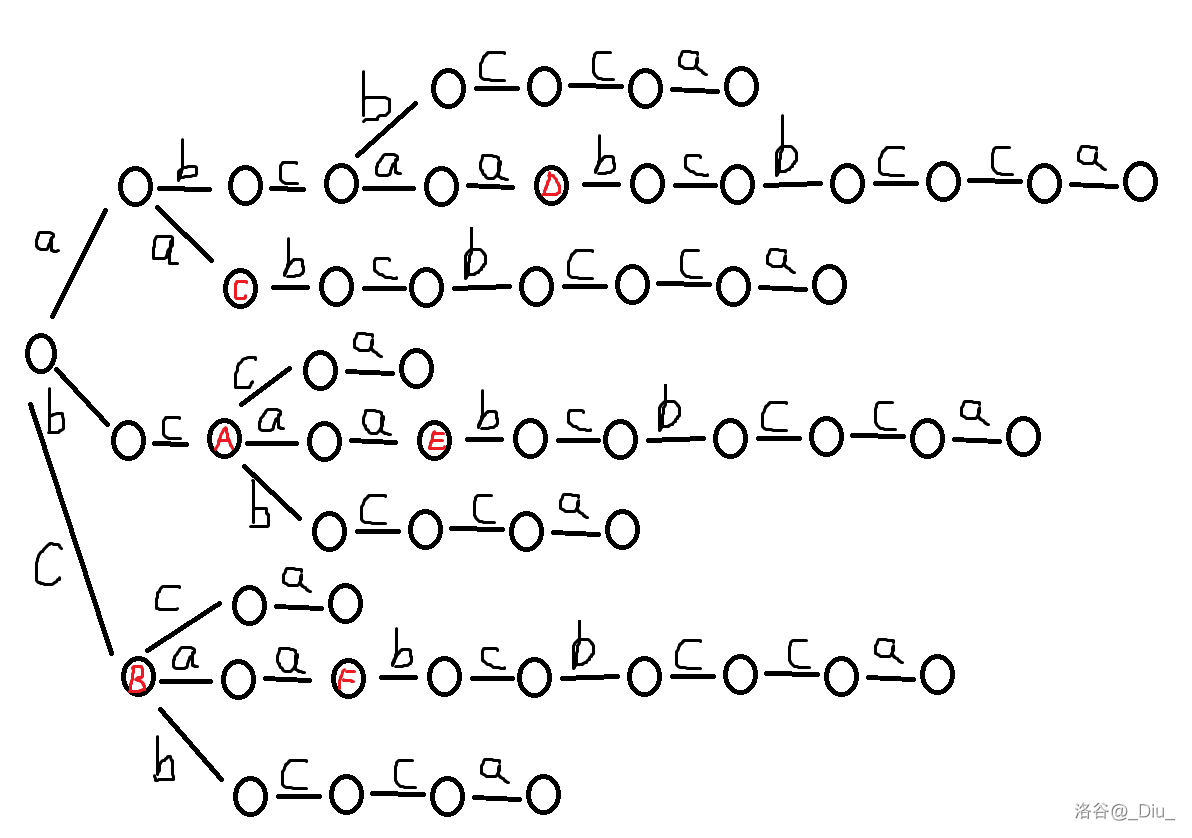
但我们发现这样做非常不好，它状态数是 \(O(n^2)\) 的。

但是，我们发现有些状态可以合并，比如上图中 A 和 B ，C 和 D 和 E 和 F 都可以合并，因为他们之后的状态是完全一样的。

endpos

对于字符串 \(s\) 的任意非空子串 \(t\)，定义集合 \(endpos(t)\) 表示每一个 \(s\) 中 \(t\) 的结束位置。例如上述字符串 abcaabcbcca，有 \(endpos(\text{abc})=\{3,6\}\)，\(endpos(\text{bc})=\{3,6,8\}\)。

由此，我们可以得到一些 \(endpos\) 的性质。（摘自 OI Wiki，略有修改）

性质 1：字符串 \(s\) 的两个非空子串 \(u\) 和 \(v\)（假设 \(|u|\le|v|\) ）的 \(endpos\) 相同，当且仅当字符串 \(u\) 在 \(s\) 中的每次出现，都是以 \(v\) 后缀的形式存在的。

很好理解，如果两者 \(endpos\) 相同，显然 \(u\) 是 \(v\) 的后缀，如果 \(u\) 还有额外出现，显然两者 \(endpos\) 不相同。

性质 2：对于字符串 \(s\) 的两个非空子串 \(u\) 和 \(v\)（假设 \(|u|\le|v|\) ），如果 \(u\) 是 \(v\) 的一个后缀，则 \(endpos(v)\subseteq endpos(u)\)，否则 \(endpos(u)\cap endpos(v)=\varnothing\)。

证明：如果 \(endpos(u)\) 与 \(endpos(v)\) 交集非空，则在某个位置字符串 \(u\) 和 \(v\) 会同时出现，所以 \(u\) 是 \(v\) 的一个后缀，所以每次 \(v\) 出现 \(u\) 就会跟着出现，所以 \(endpos(v)\subseteq endpos(u)\)。

因为可能有一些子串 \(u\)，\(v\) 的 \(endpos\) 相等，我们称他们为等价类，根据 \(endpos\) 的值，我们能够把所有子串分为若干等价类。

性质 3：对于一个 \(endpos\) 等价类，我们把里面的字符串按照长度按照不升顺序排序，此时每个子串都是它前一个子串的后缀，而且该等价类中子串长度恰好能够覆盖一整个区间 \([x,y]\)。

证明：如果 \(endpos\) 等价类只包含一个字符串，显然符合条件。

如果包含多个，那么由性质 1 可知，较短的都是较长的后缀，而且等价类中没有等长的字符串。假设该 \(endpos\) 等价类中长度最长的字符串为 \(v\)，最短的为 \(u\)，那么有 \(u\) 是 \(v\) 的后缀。对于长度在 \([|u|,|v|]\) 中的 \(v\) 的后缀们 \(w\)，根据性质 2，我们有 \(endpos(v)\subseteq endpos(w)\subseteq endpos(u)\)，又因为 \(u,v\) 同处一个等价类，所以 \(w\) 也在同一个等价类。

我们需要一个节点数比较少的自动机 SAM，这和 \(endpos\) 有什么关系呢？

我们先看看 \(endpos\) 所需要满足的条件：

  • SAM 需要是一个 DAG，我们把它的每个节点称作状态，每一条连接两个状态的边叫做状态之间的转移。

  • 图有一个源点（即上文字典树的根节点）\(t_0\)，称作初始状态，对应一个空串，它能够到达其他的所有状态。

  • 每个转移上都标有一个字符，从一个节点出发的转移上的字符均不同（满足字典树性质）。

  • 存在若干个终止状态，每一条从初始状态到终止状态的路径上字母连接起来就是字符串 \(s\) 的一个后缀。每个后缀和一条从初始状态到终止状态的路径对应。

  • 在保证上述性质的同时，要满足节点数最小。

容易发现，刚才的 trie 在满足这些性质的同时，它的节点数是最多的（

而且这样子从 \(t_0\) 出发的任意一条路径就代表着原串上的一个子串，特别地，\(t_0\) 到 \(t_0\) 的路径对应空串。

我们发现，SAM 中的某一个状态应该对应一个或多个 \(endpos\) 等价类的状态，除了初始状态（不妨称其为 \(t_0\)）之外，其他每个节点对应一个等价类。

我们可能可以利用 \(endpos\) 构造出一个 SAM？

对于 SAM 中一个不是 \(t_0\) 的状态 \(p\)，它对应一个 endpos 等价类。设 \(v\) 是这个等价类中最长的一个字符串，则其他字符串都是 \(v\) 的后缀。

我们还知道字符串 的前几个后缀（按长度降序考虑）全部包含于这个等价类，且所有其它后缀（至少有一个，即空后缀）在其它的等价类中。我们记 \(t\) 为最长的这样的后缀，然后将 \(p\) 的后缀链接连到 \(t\) 上。

也就是说，一个后缀链接 \(link(p)\) 连接到对应于 \(v\) 的最长后缀的另一个 \(endpos\) 等价类的状态。

上文提到，\(t_0\) 对应一个空串，为了方便，我们规定 \(endpos(t_0)=\{-1,0,1,\dots,|s|-1\}\)。

接下来，我们又能得到一些关于 \(link\) 的一些性质。

性质 4：所有的后缀链接能够成一颗根节点为 \(t_0\) 的树。

证明：除了 \(t_0\) 外的状态 \(p\)，后缀链接 \(link(p)\) 链接的状态对应某个或某些长度严格小于当前状态的字符串。因此，我们沿着后缀链接向上爬，总能爬到 \(t_0\)。

性质 5：由 \(endpos\) 集合构造出的树（每个非 \(t_0\) 状态的父亲是所有包含它的 \(endpos\) 集合中集合大小最小的那个）和由上述性质构造出的树相同。

首先能够想到，我们能够由 \(endpos\) 集合的从属关系构造出一颗树（性质 2）。

对于任意除 \(t_0\) 外的状态 \(p\)，根据性质 2 以及后缀链接的定义，我们能够得到 \(endpos(p)\subsetneq endpos(link(p))\)。（如果两个 \(endpos\) 相同，那么它们应该合并成一个状态）

所以，我们发现：后缀链接构造出来的树本质上是 \(endpos\) 集合构造出来的树。

构造 SAM

对于一个状态 \(p\)，我们记 \(longest(p)\) 表示它对应的 \(endpos\) 等价类字符串中最长的那个，\(len(p)\) 表示它的长度。类似地，记\(shortest(p)\) 表示它对应的 \(endpos\) 等价类字符串中最短的那个，\(minlen(p)\) 表示它的长度。

那么之前根据后缀链接的定义，有：\(minlen(p)=len(link(p))+1\)。

对于构造 SAM，我们考虑增量构造，假设我们已经构造好了一个长度为 \(n-1\) 的后缀自动机，考虑在后面增加一个字符 \(c\)。

为了保证空间复杂性，我们只存储 \(len\) 以及 \(link\)，以及每个状态的转移（可以用 map 来实现）。

struct state{
	int len,fa;//fa表示link
	map<int,int> nxt;
}st[N<<1];

为了方便，我们假设 \(t0\) 的 \(len=0,link=-1\)。（指向虚拟状态）

算法流程大致如下：

令 \(lst\) 表示长度为 \(n-1\) 的字符串所对应的状态（初始 \(lst=0\)），我们新建一个状态 \(cur\)，表示新的整个字符串。

此时我们把 \(len(cur)\) 赋值为 \(len(lst)+1\)，此时还不知道 \(link(cur)\) 的值。

int cur=++tot;
st[cur].len=st[lst].len+1;

接下来我们按照以下流程进行，从状态 \(lst\) 开始。如果没有字符 \(c\) 的转移，就说明该状态原来并不对应以 \(c\) 为结尾的 \(endpos\)，我们添加一个从该状态到 \(cur\)，字符为 \(c\) 的转移，并便利其后缀链接。如果有，那么就停下来，并记录这个状态。如果没有，到达了虚拟状态，我们就将 \(link(cur)\) 赋值为 \(0\)，并且不参与接下来的连边活动。

我们希望能够添加一个字符 \(c\) 到达新状态 \(cur\)，因为不能与原来状态冲突，所以找到了原来存在 \(c\) 的状态就必须停止。

如果没有出现过，就直接连 \(t_0\) 即可。

int p=lst;
while(p!=-1&&!st[p].nxt.count(c))st[p].nxt[c]=cur,p=st[p].fa;
if(p==-1)st[cur].fa=0;

接下来，我们记状态 \(p\) 通过转移字符 \(c\) 到达的状态是 \(q\)。

若 \(len(p)+1=len(q)\)，我们只需要将 \(link(cur)\) 也赋值为 \(q\) 即可。

因为此时 \(longest(q)\) 就是 \(x+c\)（\(x\) 表示某个字符串，可能为空），而且这个字符串作为原串的某个子串已经出现过了，所以我们一连就可以了。

int q=st[p].nxt[c];
if(st[p].len+1==st[q].len)st[cur].fa=q;

否则我们需要把 \(q\) 拆成两个点，原来的连 \(q\)，新增的连新的点。

这时我们可以创建一个新的状态 \(cl\)，然后把 \(q\) 除了 \(len\) 以外的信息赋值过来，并把 \(len(cl)\) 赋值为 \(len(p)+1\)。

复制完后，我们让 \(cur\) 和 \(q\) 都指向 \(cl\)。

最终我们需要使用后缀链接从状态 \(p\) 往回走，只要存在一条通过状态 \(p\) 到状态 \(q\) 的转移，就将该转移重定向到状态 \(q\)。

else{
    int cl=++tot;
    st[cl].fa=st[q].fa;
    st[cl].nxt=st[q].nxt;
    st[cl].len=st[p].len+1;
    while(p!=-1&&st[p].nxt[c]==q)st[p].nxt[c]=cl,p=st[p].fa;
    st[q].fa=st[cur].fa=cl;
}

完成这个过程之后，需要重新赋值 \(lst\)。

完整代码大致如下。

struct state{
	int len,fa;
	map<int,int> nxt;
}st[N<<1];
int n,q,tot,lst;
int d[N<<1];
char s[N];
void insert(int c,int lst){
	int cur=++tot;
	st[cur].len=st[lst].len+1;
	int p=lst;
	while(p!=-1&&!st[p].nxt.count(c))st[p].nxt[c]=cur,p=st[p].fa;
	if(p==-1)st[cur].fa=0;
	else{
		int q=st[p].nxt[c];
		if(st[p].len+1==st[q].len)st[cur].fa=q;
		else{
			int cl=++tot;
			st[cl].fa=st[q].fa;
			st[cl].nxt=st[q].nxt;
			st[cl].len=st[p].len+1;
			while(p!=-1&&st[p].nxt[c]==q)st[p].nxt[c]=cl,p=st[p].fa;
			st[q].fa=st[cur].fa=cl;
		}
	}
	lst=cur;
}

时间复杂度我不太会证，我们发现每次操作会增加 \(1\) 或 \(2\) 个点，所以空间复杂度是线性的。

回到原题，我们发现做完这些操作之后，直接搜一遍便利 SAM，统计答案就可以了。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int N=1e6+10;
struct state{
	int len,fa;
	map<int,int> nxt;
}st[N<<1];
int n,tot,lst;
int t,k;
ll f[N<<1];
vector<int> G[N<<1];
char s[N];
void init(){
	st[0].len=tot=lst=0,st[0].fa=-1;
}
void insert(int c){
	int cur=++tot;f[cur]=1;
	st[cur].len=st[lst].len+1;
	int p=lst;
	while(p!=-1&&!st[p].nxt[c])st[p].nxt[c]=cur,p=st[p].fa;
	if(p==-1)st[cur].fa=0;
	else{
		int q=st[p].nxt[c];
		if(st[p].len+1==st[q].len)st[cur].fa=q;
		else{
			int cl=++tot;
			st[cl].fa=st[q].fa;
			st[cl].nxt=st[q].nxt;
			st[cl].len=st[p].len+1;
			while(p!=-1&&st[p].nxt[c]==q)st[p].nxt[c]=cl,p=st[p].fa;
			st[q].fa=st[cur].fa=cl;
		}
	}
	lst=cur;
}
int dfs(int u){
	for(int i=0;i<G[u].size();i++)f[u]+=dfs(G[u][i]);
	return f[u];
}
signed main(){
	scanf("%s",s+1),n=strlen(s+1);
	init();
	for(int i=1;i<=n;i++)insert(s[i]-'a');
	for(int i=1;i<=tot;i++)G[st[i].fa].push_back(i);
	dfs(0);
	ll ans=0;
	for(int i=0;i<=tot;i++)if(f[i]!=1)ans=max(ans,st[i].len*f[i]);
	printf("%lld\n",ans);
}

评测记录

同时，用这个方法，我们可以把 广义 SAM 和不同子串个数 全部过了。

ll dfs(int x){
	if(d[x])return d[x];
	for(int i=0;i<26;i++){
		if(st[x].nxt.count(i))d[x]+=dfs(st[x].nxt[i]);
	}
	return ++d[x];
}

广义 SAM 评测记录

不同子串个数评测记录

后缀自动机的运用

建议把刚刚后缀数组的全部用后缀自动机做一遍

例 1：P3975 [TJOI2015]弦论

题目大意：求一个字符串第 \(k\) 小子串

在 SAM 上跑 dp，可以尝试自己推一下。

int t,k,f[N<<1],g[N<<1];
vector<int> G[N<<1];
bool vis[N<<1];
char s[N];
int dfs(int u){
	for(int i=0;i<G[u].size();i++)f[u]+=dfs(G[u][i]);
	return f[u];
}
int dfs2(int x){
	if(vis[x])return g[x];
	vis[x]=1;
	for(int i=0;i<26;i++){
		if(st[x].nxt[i])g[x]+=dfs2(st[x].nxt[i]);
	}
	return g[x];
}
void Dfs(int x,int k){
	if(k<=f[x])return;
	else k-=f[x];
	for(int i=0;i<26;i++){
		if(!st[x].nxt[i])continue;
		int v=st[x].nxt[i];
		if(k>g[v])k-=g[v];
		else{
			printf("%c",(char)(i+'a'));
			Dfs(v,k);
			return;
		}
	}
}
signed main(){
	scanf("%s%d%d",s+1,&t,&k),n=strlen(s+1);
	init();
	for(int i=1;i<=n;i++)insert(s[i]-'a');
	for(int i=1;i<=tot;i++)G[st[i].fa].push_back(i);
	if(t){
		dfs(0);
		for(int i=1;i<=tot;i++)g[i]=f[i];//不要求本质不同，有多少个算多少个
	}else for(int i=1;i<=tot;i++)g[i]=f[i]=1;//要求本质不同，一种只能算一个
	f[0]=0;
	dfs2(0);
	if(k>g[0])puts("-1");
	else Dfs(0,k);
}

评测记录

接下来是几道我可能都没做的练习。

CF914F Substrings in a String ps：可以根号分治+SAM。但是数据过水 bitset 暴打标算

CF1037H Security ps：SAM 和线段树，SA 和主席树等等，做法很多。

P4770 [NOI2018] 你的名字 ps：SAM 和线段树合并结合。

Oiclass 4088 字符串 ps：可以用后缀自动机做，也可以用后缀数组+回滚莫队做。

P4070 [SDOI2016]生成魔咒