上机练习十一
导航：复试上机历年真题，题目未搜集全
十四：2003 十三：2004
十二：2005 十一：2006
十：2007 九：2008
八：2009 七：2012
六：2013 五：2014
四：2015 三：2017
二：2018 一：2019
十一、2006
有很10年以前的复试上机题有很多与10年之后的相似，并且难度也感觉大了点
1、相约2006
题目：
相约 2006：2006 是一个合数，求出此合数最多由多少个最小不同质数和组成，并按要求从小到大输出这些质数。
思路：
我觉得这是这几年题目最难的一道，这个题目跟17年的求连续素数的和等于某一值不一样，如果为了满足最多的最小质数和，则需要从右往左遍历贪心求连续的素数和，到最后会发现，无法求得一个方案，结果差1，而如果将1当做最小的素数，填补这个差值，恰好可以满足条件。但是显然1不是素数。
错解代码：
#include<stdio.h>
#include<math.h>
#include<string.h>
#include<algorithm>
using namespace std;
//出错
//sums=2127, diff=121
//sums-diff=2006
//diff=8, a[0]=113
//diff=1, a[1]=7
//需要剔除 7
//需要剔除 113
//最后diff是1不是0
const int maxn=2009;
int num=0;
int p[maxn]={0}, prime[maxn]={0};
void primeTable()
//求素数表存储在prime数组中
{
int i;
for(i=2;i<maxn;i++)
{
if(p[i]==0)
{
prime[num++]=i;
for(int j=2*i;j<maxn;j+=i)
p[j]=1;
}
}
}
int main()
{
int i, j;
int sums, k;
sums = 0;
primeTable();
// for(int i=0;i<num;i++)
// printf("%d ", prime[i]);
for(k=0;k<num;k++)
{
sums += prime[k];
if(sums>=2006)
break;
}//跳出循环时，i指向prime数组和相应的最后一个元素
if(sums==2006)//刚好求得一定prime数组中下标为0,1,2...i的元素和符合要求
{
for(i=0;i<=k;i++)
printf("%4d\n", prime[i]);
}
else if(sums>2006)
{
int a[maxn]={0};//prime表中需要剔除的元素
int diff, t;
t=0;//用t来记录剔除元素表a中的元素
diff = sums-2006;
printf("sums=%d, diff=%d\n",sums, diff);
printf("sums-diff=%d\n",sums-diff);
for(i=k;i>=0&&diff!=0;i--)//找到需要剔除的元素并且放入数组a中
{
if(prime[i]==diff||(prime[i]<diff&&prime[i+1]>diff))
{
diff = diff-prime[i];
a[t++] = prime[i];
printf("diff=%d, a[%d]=%d\n", diff, t-1, prime[i]);
}
}
printf("diff=%d\n", diff);
int flag;
int num = 1;
for(i=0;i<=k;i++)
{
printf("第%d个：", num++);
flag=0;//如果prime[i]剔除数组a中，则flag=1，默认不需要剔除
for(j=0;j<t;j++)
if(prime[i]==a[j])
flag=1;
if(flag==0)//不需要剔除，正常输入
printf("%4d\n", prime[i]);
else if(flag==1)
printf("需要剔除%4d\n", prime[i]);
}
}
return 0;
}
没有想到求满足最小的质数和，但是可以用动态规划求出来一种方案。
- 首先先素数打表
- 用动态规划求从数组中取出几个数满足某一个和S
- 再根据条件找出这几个数
动态规划的过程就是给定一个正整数s, 判断一个数组arr中，是否有一组数字加起来等于s。可以参考传送门：动态规划
动态规划代码：
#include<stdio.h>
#include<algorithm>
using namespace std;
const int maxn=2009;
int num=0;
int p[maxn], prime[maxn];//prime数组用来存放素数
void primeTable()//素数表
{
for(int i=2;i<maxn;i++)
{
if(p[i]==0)//p[i]=0说明i是素数
{
prime[num++] = i;//i是素数放入prime数组
for(int j=2*i;j<maxn;j+=i)
{
p[j] = 1;//i为素数，则i的倍数都不是素数
}
}
}
}
void cal(int arr[], int n, int S)
{
//方案是否可行数组
int dp[n][S+1]={0};
//边界值初始化
for(int i=0;i<n;i++)
dp[i][0] = 0;
for(int j=0;j<S+1;j++)
dp[0][j] = 0;
dp[0][arr[0]] = 1;
//状态转移方程
for(int i=1;i<n;i++)
for(int j=1;j<S+1;j++)
{
if(arr[i]>j)
dp[i][j] = 0;
else
dp[i][j] = dp[i-1][j] || dp[i-1][j-arr[i]];
}
if(dp[n-1][S]==1)//说明方案可行
{
int i=n-1, k=0;
int sol[n]={0};
while(i>=0)
{
if(dp[i][S]==1&&dp[i-1][S]==0)
//如果用前i-1个数字无法组成数S，而前i个数可以组成数字S，那么说明第i个数肯定要选
{
sol[k++] = arr[i];
S -= arr[i];
}
if(S==0)
break;
i--;
}
int sums=0;
for(int i=0;i<k;i++)
{
sums+=sol[i];
printf("%d", sol[i]);
if(i<k-1)
printf("+");
else
printf("=%d\n", sums);
}
}
}
int main()
{
int S=2006;
int sums, n;
sums=0; n=0;
primeTable();
for(int i=0;i<num;i++)
{
sums+=prime[i];
n++;
if(sums>S)
break;
}
cal(prime, n, S);
return 0;
}
2、二叉排序树
题目：
二叉排序树：
①要求建立以二叉链表方式存储的二叉排序树。
②按树状输出（如下图）；
③输出结点值递减结果。
测试数据：H，A，X，F，T，B，R，@（@结束标志）
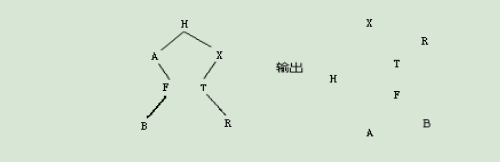
此例输出结点值递减结果 X R T H F B A
代码：
#include<stdio.h>
typedef struct BSTNode{
char data;
struct BSTNode *lchild, *rchild;
}BSTNode, *BSTree;
void insert(BSTree *bst, char ch)//插入节点
{
if(*bst==NULL)
{
BSTNode *q;
q = new BSTNode;
q->data = ch;
q->lchild = NULL; q->rchild = NULL;
*bst = q;
}
else
{
if(ch>(*bst)->data)
insert(&((*bst)->rchild), ch);
else if(ch<(*bst)->data)
insert(&((*bst)->lchild), ch);
}
}
void creatBST(BSTree *bst)//创建二叉排序树
{
char ch;
*bst=NULL;
while((ch=getchar())!=NULL&&ch!='@')
{
insert(bst, ch);
}
}
void reversePrint(BSTree bst)//逆序输出
{
if(bst!=NULL)
{
reversePrint(bst->rchild);
printf("%c", bst->data);
reversePrint(bst->lchild);
}
}
void printLayer(BSTree bst, int layer)//层级输出
{
if(bst!=NULL)
{
printLayer(bst->rchild, layer+1);
for(int i=0;i<layer;i++)
printf("\t");
printf("%c\n", bst->data);
printLayer(bst->lchild, layer+1);
}
}
int main()
{
BSTree bst;
bst = new BSTNode;
creatBST(&bst);
printf("逆序输出：");
reversePrint(bst);
printf("\n树状输出：\n");
printLayer(bst, 0);
return 0;
}
3、二进制加1
题目：
二进制数加 1
建立一个带头结点的线性链表，用以存放输入的二进制数，链表中每个结点的 data 域存放一个二进制位。
在此链表上实现对二进制数加 1 的运算，并输出运算结果。
测试数据 1: 1010011，输出1010100
测试数据 2 1111， 输出10000
要找到最后一个为0的链表节点，将该节点的值改为1，该节点的后继结点变为0；
如果链表中节点值全为1，则需要新建一个节点插入首部
代码：
#include<stdio.h>
#include<string.h>
typedef struct LNode{
int data;
struct LNode *next;
}LNode, *Linklist;
void creatLinklist(Linklist L, char str[])//尾插法创建二进制链表
{
int len=strlen(str);
LNode *r, *q;
L->next = NULL;
r = L;
for(int i=0;i<len;i++)
{
q = new LNode;
q->data = str[i]-'0';
q->next = NULL;
r->next = q;
r = r->next;
}
}
void travel(Linklist L)//遍历链表
{
LNode *r;
r = L->next;
while(r!=NULL)
{
printf("%d", r->data);
r = r->next;
}
printf("\n");
}
void cal(Linklist L)
//要找到最后一个为0的链表节点，将该节点的值改为1，该节点的后继结点变为0；
//如果链表中节点值全为1，则需要新建一个节点插入首部
{
LNode *r, *q;
q = L; r = q;
while(r!=NULL)
{
if(r->data==0)
q = r;//q指向最后一个值为0的节点
r = r->next;
}
if(q==L)//链表节点全是1 ，新建一个节点插入首部
{
LNode *m;
m = new LNode;
m->next = q->next;
q->next = m;
q = m;
}
q->data = 1;
r = q->next;
while(r!=NULL)//修改值为0
{
r->data = 0;
r = r->next;
}
}
int main()
{
char str[100];
gets(str);
Linklist L;
L = new LNode;
creatLinklist(L, str);
printf("加1前：");
travel(L);
cal(L);
printf("加1后：");
travel(L);
return 0;
}
4、哈希表
题目：
构造哈希表
设哈希函数为 H（X）=i/2，其中 i 为关键字中的第一个字母在字母表中的序号，处理冲突可选用线性探测法。要求编程完成：
构造哈希表：在地址空间为0-12 ，对以下关键字序列（Jan,Feb,Apr,May,Jun,Jul,Aug,Sep,Oct）建哈希表
用程序自动计算求出在等概率的情况下查找成功与不成功的平均查找长度。
代码：
#include<stdio.h>
#include<string.h>
#include<math.h>
#include<algorithm>
using namespace std;
const int maxn=20;
const int n=13;
typedef struct record{
char a[maxn];
int sign;//用于标识该记录是否被使用
record(){
sign = -1;//默认为-1，表示未被使用
}
}record;
int calHashRes(char a[])
//哈希函数为H(X)=i/2， i为关键字中的第一个字母在字母表总的序号
{
int k;
k = a[0]-'A'+1;
k /= 2;
return k;
}
double successTimes(char s[maxn][maxn], record hashTable[])//要加hashTable[]括号
//查找成功的平均比较次数
{
double res, num, sums;
int i, k;
sums = 0;
for(i=0;i<9;i++)
//逐个记录计算查找长度，并累加
{
num = 1;
k = calHashRes(s[i]);
while(strcmp(hashTable[k].a, s[i])!=0)
//没有找到，一直用线性探测
{
num++;
k = (k+1)%n;
}
sums += num;
}
res = sums/9;//查找成功时除以元素个数
return res;
}
double unsuccessTimes(record hashTable[])
//查找失败的平均比较次数
{
double res, num, sums;
int i, j;
sums = 0;
for(i=0;i<n;i++)
//哈希表逐个单位做查找失败长度统计，0,1,2...12
{
num = 1;
j = i;
while(hashTable[j].sign!=-1)
//知道找到空单元
{
num++;
j = (j+1)%n;
}
sums += num;
}
res = sums/n;//查找失败时除以表长
return res;
}
int main()
{
int i, k;
char s[maxn][maxn] = {
"Jan","Feb","Apr","May","Jun","Jul","Aug","Sep","Oct"
};
record hashTable[n];
for(i=0;i<9;i++)//生成hashTable
{
k = calHashRes(s[i]);
while(hashTable[k].sign!=-1)
k = (k+1)%n;//可选用地址空间为0-12，共13个
if(hashTable[k].sign==-1)//找到可放位置
{
strcpy(hashTable[k].a, s[i]);
hashTable[k].sign = 1; //并做标注
}
}
for(i=0;i<13;i++)
{
if(hashTable[i].sign!=-1)
printf("%2d，%s\n", i, hashTable[i].a);
}
printf("成功的比较次数为%5.2f\n", successTimes(s, hashTable));
printf("失败的比较次数为%5.2f\n", unsuccessTimes(hashTable));
return 0;
}
汇总链接
posted on 2020-04-18 11:14 weilanhanf 阅读(411) 评论(0) 编辑 收藏 举报
