ACM-Expanding Rods

A - Expanding Rods

Time Limit:1000MS     Memory Limit:30000KB     64bit IO Format:%I64d & %I64u

Submit Status

Description

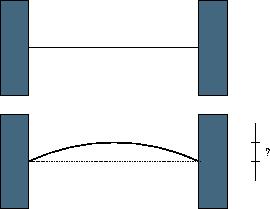
When a thin rod of length L is heated n degrees, it expands to a new length L'=(1+n*C)*L, where C is the coefficient of heat expansion. 
When a thin rod is mounted on two solid walls and then heated, it expands and takes the shape of a circular segment, the original rod being the chord of the segment. 

Your task is to compute the distance by which the center of the rod is displaced. 

Input

The input contains multiple lines. Each line of input contains three non-negative numbers: the initial lenth of the rod in millimeters, the temperature change in degrees and the coefficient of heat expansion of the material. Input data guarantee that no rod expands by more than one half of its original length. The last line of input contains three negative numbers and it should not be processed.

Output

For each line of input, output one line with the displacement of the center of the rod in millimeters with 3 digits of precision. 

Sample Input

1000 100 0.0001
15000 10 0.00006
10 0 0.001
-1 -1 -1

Sample Output

61.329
225.020
0.000

集训的第一个题，我竟然连圆的几个公式都不记得了，好吧~ 

二分，综合两个公式，然后，精度弄高点，不然就wa了

#include <iostream>
#include <cstdio>
#include <cmath>

using namespace std;

int main()
{
    double n,c,l;
    while(~scanf("%lf %lf%lf",&l,&n,&c))
    {

        if(l < 0 && n < 0 && c < 0)
            break;
        double ll = (1 + n * c) * l;
//        printf("%.3lf",l);
        double low, high ,mid , r;
        low  = 0;
        high = l / 2;

        while (high - low > 0.000001)
        {
            mid =(low  + high)/2;
            r  =((l * l)+(4*mid *mid ))/ (8 * mid );
            if ((2 * r * asin(l / (2*r)) < ll))
                low = mid;
            else
                high = mid;

        }
        printf ("%.3lf\n",mid);
    }
    return 0;
}

61.329
225.020
0.000