math-2023-07-27
1、图片截取自《机器学习第二阶段：机器学习经典算法（2）--贝叶斯算法》视频的《2.贝叶斯推导实例》中06:31，第一个问题是关于贝叶斯的理解（主要针对相交特性）：（1）http://www.360doc.com/content/20/0822/17/773384_931659968.shtml，（2）https://zhuanlan.zhihu.com/p/32825019；第二个问题是关于贝叶斯和似然估计的区别和联系（为了了解贝叶斯在什么情况下用）：https://www.cnblogs.com/liguangsunls/p/7347211.html。
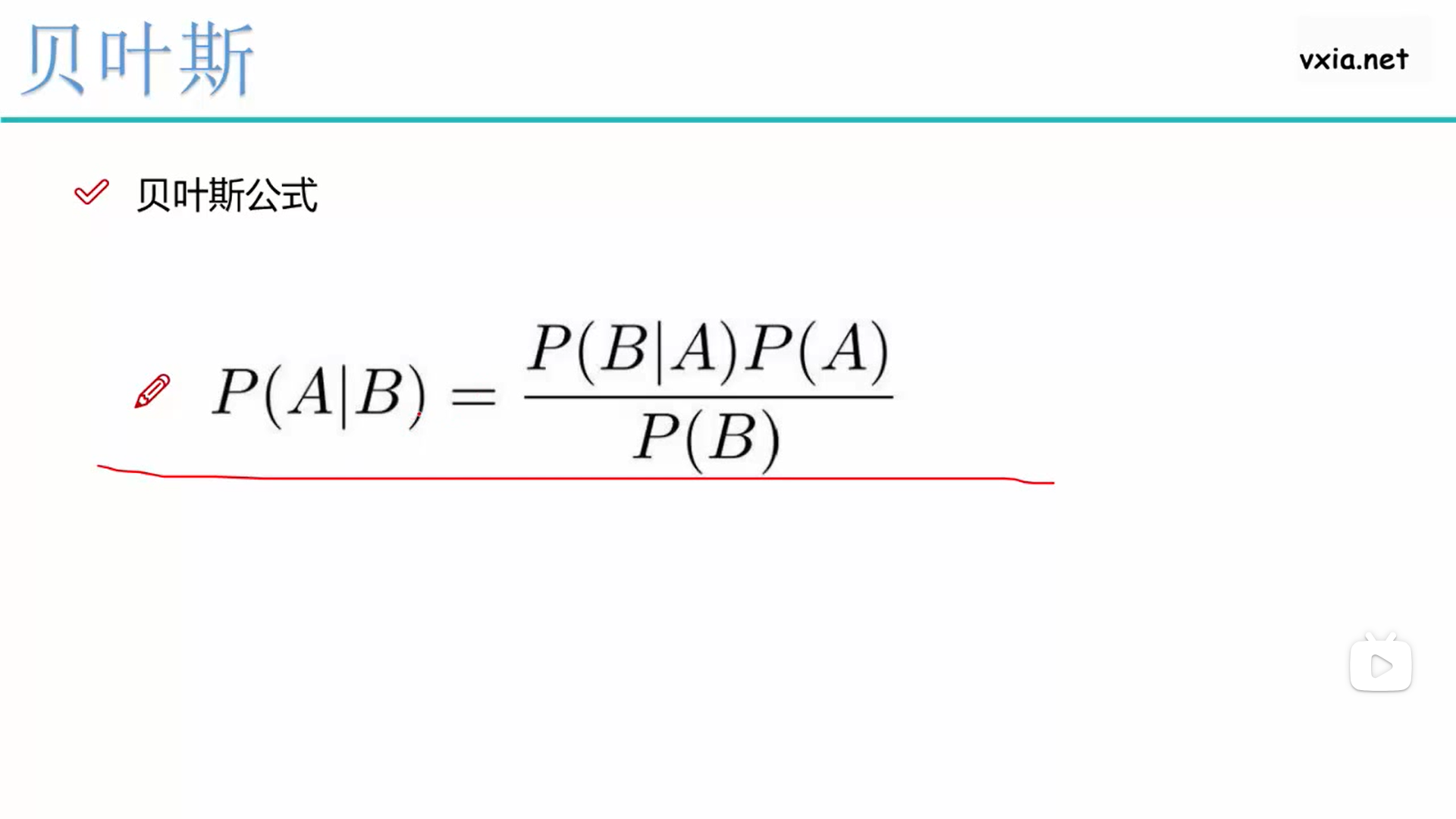
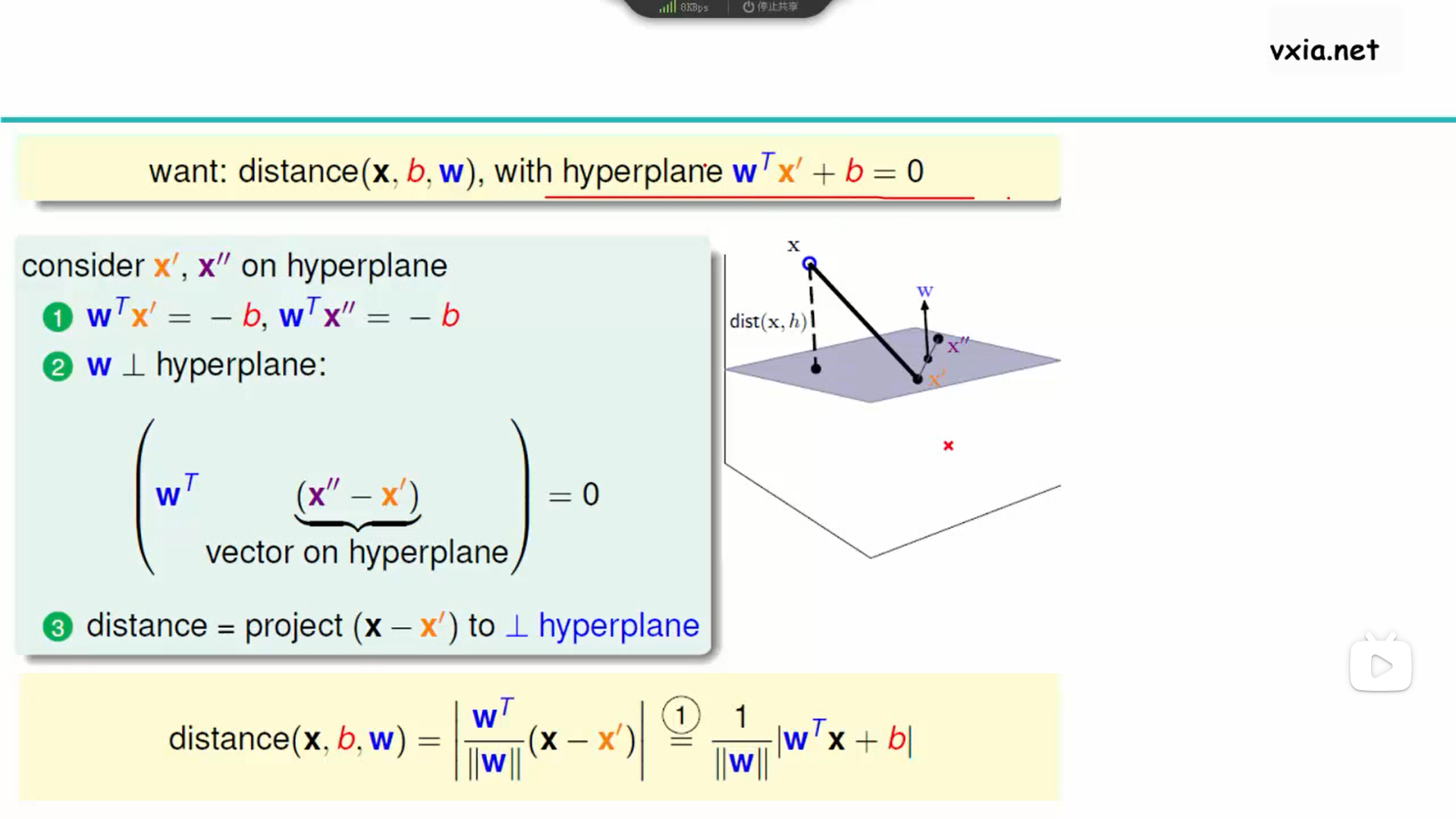
2、图片截取自《机器学习第二阶段：机器学习经典算法（5）--支持向量机》视频的《2.支持向量机求解目标》中00:27，首先，对于为什么用超平面的理解：因为对二维平面的数据点进行分类可以使用一条线进行划分，但是对于三维空间的点进行划分就需要用到平面，依此类推，在多维空间中的点划分就自然而然需要用到超平面了，接下来的问题是这个超平面的公式WTX'+b=0是怎么来的？目前还没有找到合乎逻辑而且比较通俗的证明。
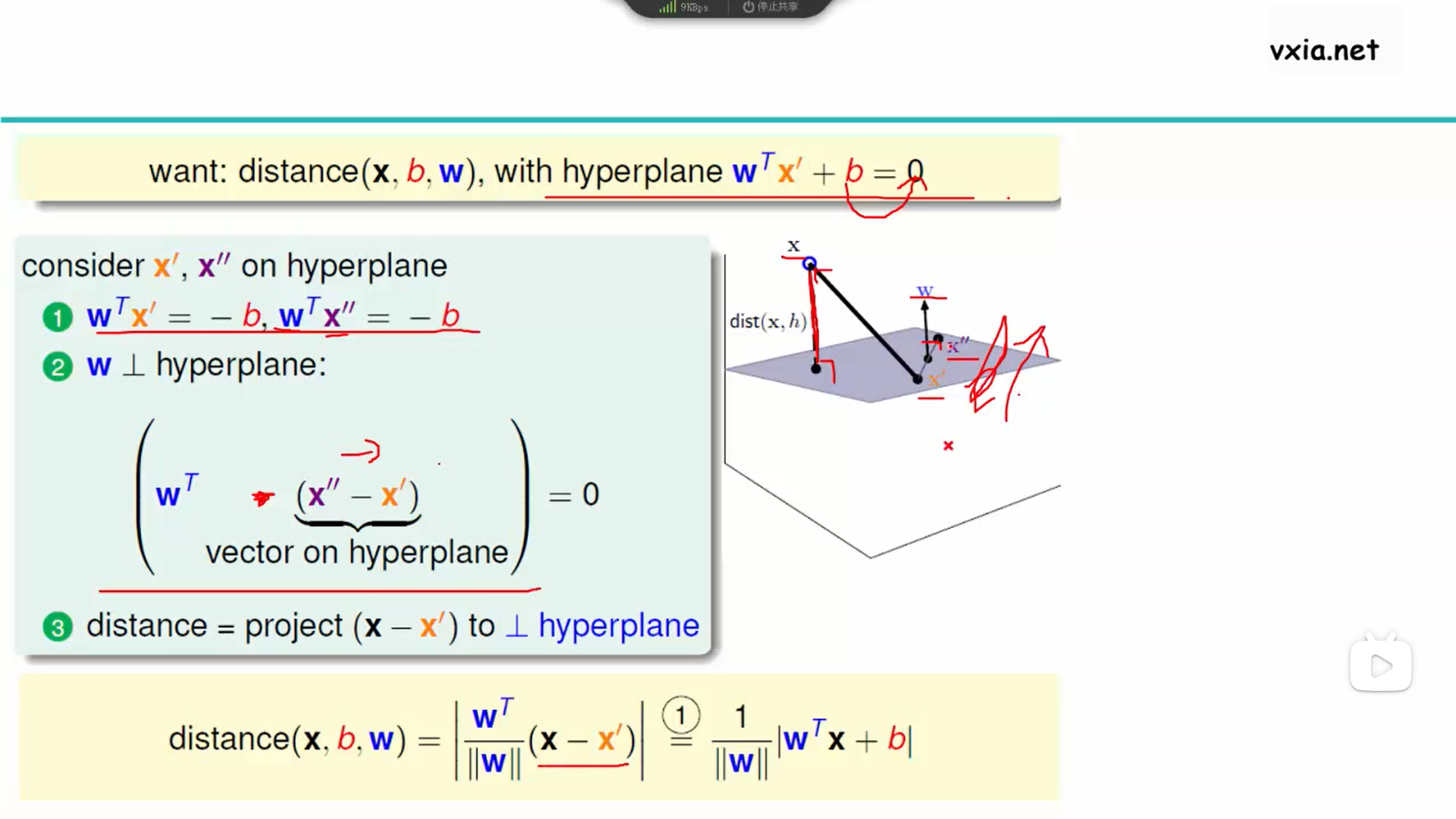
3、图片截取自《机器学习第二阶段：机器学习经典算法（5）--支持向量机》视频的《2.支持向量机求解目标》中03:35，为什么样本点x到超平面的距离distance(x,b,w)是用w的单位方向乘以(x-x')？查的过程中想起了一个被忽略的重要前提，那就是为什么w会是法向量？可以参考：（1）https://blog.csdn.net/wyssailing/article/details/112425386，（2）https://blog.csdn.net/deeplearningcc/article/details/127520134。
4、图片截取自《机器学习第二阶段：机器学习经典算法（5）--支持向量机》视频的《3.支持向量机目标函数求解》中09:22，第一点，下图拉格朗日乘子法的第二项提取了负号之后变换得来；第二点，对于为什么要使L(w,b,α)中α最大，这是因为当拉格朗日乘子法整个第二项由α和((yi(wT·φ(xi)+b)-1)构成，在构造L(w,b,α)之前已经有w,b要求最小的前提，所以((yi(wT·φ(xi)+b)-1)倾向于变得越小，如果这时α越大那么整个第二项也越大，而第二项前面还有一个负号，那么第二项减的越多则越能满足L(w,b,α)整个式子最小的要求，对偶问题在视频中有讲，即一个函数最小的那个极大值一般来说总是大于极小值当中最大的那个，引入对偶是为了协助数学求解（还有后面的对α由求取极大值转换成求极小值也是，如果不清楚某一步变换起到了什么作用或者其对最终结果造成的那个影响是什么就容易陷进去）；所以第三点，这里更关心的问题是α的含义是什么？（其实类似于梯度下降的学习率，即步长，但会有个疑问就是为什么αi要取≥0？）还有为什么构造L(w,b,α)时可以直接加上各个α·g(x)？可以参考：https://mp.weixin.qq.com/s?__biz=MzI1MjQ2OTQ3Ng==&mid=2247489935&idx=1&sn=31290c09d6aa0baf2bf6cb59475b2ddd&chksm=e9e21004de9599125a2ec0a79938a123f4291b3fac89d8b7ec72e318c7296e2a05b7dcfda07d&scene=27，其中的“一、关于拉格朗日乘子法和KKT条件”中“1.关于拉格朗日乘子法”；第四点，如果到最后真的已经求出来了w，当||w||取得最小时（譬如0）或者最大时会发生什么事情，换句话来说就是几何平面的情形是什么样的？可参考：https://zhuanlan.zhihu.com/p/270298485，其中的“2.1最小间隔定义”。
5、图片截取自《机器学习第二阶段：机器学习经典算法（5）--支持向量机》视频的《4.支持向量机求解例子》中02:38，第四行画红线式子怎么得来的？目前没有找到展开相乘的形象化例子，只按式子来看的话为了避免冲突将x改写成了j这其实也不妨碍理解。
6、图片截取自《机器学习第二阶段：机器学习经典算法（5）--支持向量机》视频的《4.支持向量机求解例子》中05:43，极大值转换成求极小值的思路？这里的转换是借助了相反数，即不直接求极大值而是直接求了相反数的极小值。
7、图片截取自《机器学习第二阶段：机器学习经典算法（5）--支持向量机》视频的《6.软间隔支持向量机》中05:46，公式L(w,b,ξ,α,μ)的第四项怎么来的？（KKT条件）对于松弛因子和惩罚变量以及（核函数相关的）线性可分的实际含义理解？可参考：（1）https://www.cnblogs.com/jerrylead/archive/2011/03/18/1988415.html，其中的“9 规则化和不可分情况处理（Regularization and the non-separable case）”，（2）http://www.blogjava.net/zhenandaci/archive/2009/03/15/259786.html。
