动态规划1

 

 

递归写法

或者

 

也会很多重叠的问题

1、记忆化搜索

 

2、动态规划

 

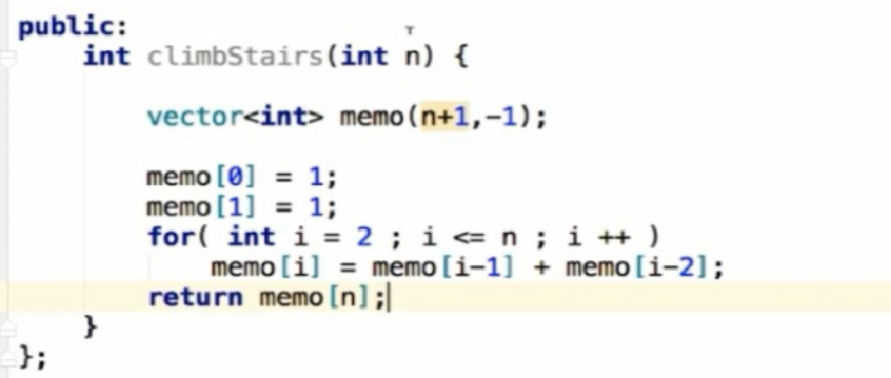
斐波那契数列，就是从爬楼梯里面总结出来的。

 

经典的动态规划问题

 

有时候记忆化搜索会比较难写出递归的代码，比如这道题。

 

求【2】的最短路径，其实就i是求【3】【4】里面的最短路径，就是求【6】，【5】，【7】的最短路径，然后最后一列的最短路径就是他自己。

这样会有重复的部分，重复的就放在记忆化搜索数组里面就好。

其实这个递归代码并不好写。

那么记忆化想出来了，怎么改成动态规划？

从基本问题入手，可以想到，对于第三层来说，最短路径就是当前数字+下一层相邻里面最小的数字。

对第二层来说，也是这样。

所以就可以写出一个循坏的代码（动态规划更像循环）
可以用一个数组，记录每一行的最小值，但是这样好像比较麻烦，

干脆直接覆盖原数组，因为算出最小值之后，原来的数字就没有用了。

我的代码。

int len = triangle.size();

        //最后一行不用改

        //从倒数第二行开始
        for(int i=len-2;i>=0;i--){

            List<Integer> current = triangle.get(i);
            List<Integer> next = triangle.get(i+1);

            //看他的排布状况，不是开头对齐排列的，相邻好像就+0，+1
            //当前这个数字的最短路径 = 当前数字+min{last(当前+0，当前+1)}

            int index = current.size();

            for(int j=0;j<index;j++){

                //因为下一行是比上一行长的，所以最后一个肯定不会溢出
                int now = current.get(j);

                int now0 = next.get(j);
                int now1 = next.get(j+1);

                if(now0<now1){
                    current.set(j,now+now0);
                }else{
                    current.set(j,now+now1);
                }

            }

        }

        //遍历完以后，当前第一列的那个元素就是最短路径

        return triangle.get(0).get(0);

一次通过美滋滋

 

 

 

这个题其实也很简单。

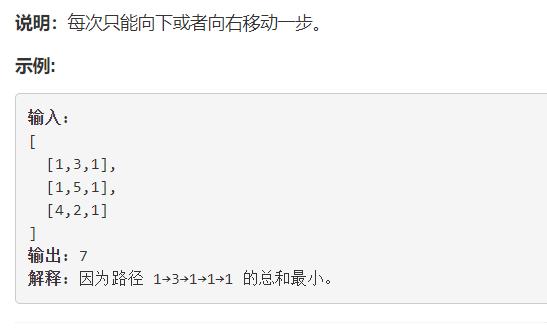
求a11的最短路径，其实就是求a12和a21的最短路径，然后选这里面最小的就是了。

然后递归代码也不好写。

怎么办呢？那就从最后往上加上去。

最后一行没法向下走，所以最后一行的最短路径都是直接加上右边。

最右列的元素，就是直接加上下边。

然后直接覆盖原值。

所以对于普通元素，就是看右边和下边哪个小就好了。

最后【0】【0】就是答案

 //从最后一个算起
        int row = grid.length-1;
        int column = grid[0].length-1;

        for(int i=row;i>=0;i--){

            for (int j=column;j>=0;j--){

                if(i==row&&j==column){
                    continue;
                }else if (i==row){
                    //如果是最后一行，就没法向下走了，那么最短路径就是直接加上右边
                    int right = grid[i][j+1];
                    grid[i][j]+=right;
                }else if(j==column){
                    //如果是最右一列，就没法往右走了，那么最短路径就是直接加上下面
                    int next = grid[i+1][j];
                    grid[i][j]+=next;
                }else {
                    //选右边的下边里，最短的路径
                    int right = grid[i][j+1];
                    int next = grid[i+1][j];

                    if(right<next){
                        grid[i][j]+=right;
                    }else{
                        grid[i][j]+=next;
                    }

                }

            }

        }

        return grid[0][0];

一次通过美滋滋