NG机器学习笔记

第一章 初始机器学习

搜索、相片分类、反垃圾邮件这些应用，都使用了机器学习算法。

简单来说就是机器自己去学习该怎么做。

 

那些地方使用了机器学习

1、无法人工编写的程序。

无人直升机、无人驾驶、围棋等等。

直接通过人去编写相关程序，根本无法实现，最好的方式就是机器自己去学习怎么解决这些问题。

 

2、推荐算法以及那些个人定制的软件

不可能为每一个人写一套推荐算法，邮件分类算法。

 

定义

经验E： 下了N次棋/观察邮件分类

任务T：下棋/分类邮件

性能量度P：胜率/邮件分类正确率

 

监督学习

给定数据集去训练

样本->正确答案

回归问题，预测房价

离散01、分类问题

可见，机器学习不能保证预测结果百分百正确。

 

非监督学习

聚类算法：新闻分类、可能互相认识的好友

分类出叠加的声音、人声、音乐声，比如全民K哥的过滤杂音等等

这个算法不复杂，只需要一行。

业内一般使用octave验证可行性，再用迁移到C++或者java

 

感想

关键是怎样将机器学习算法用在实际的项目中

机器学习用途还是很广的

机器学习很有趣！

 

第二章

 

监督学习，每个例子有个正确的答案。

回归问题，也就是预测

 

 

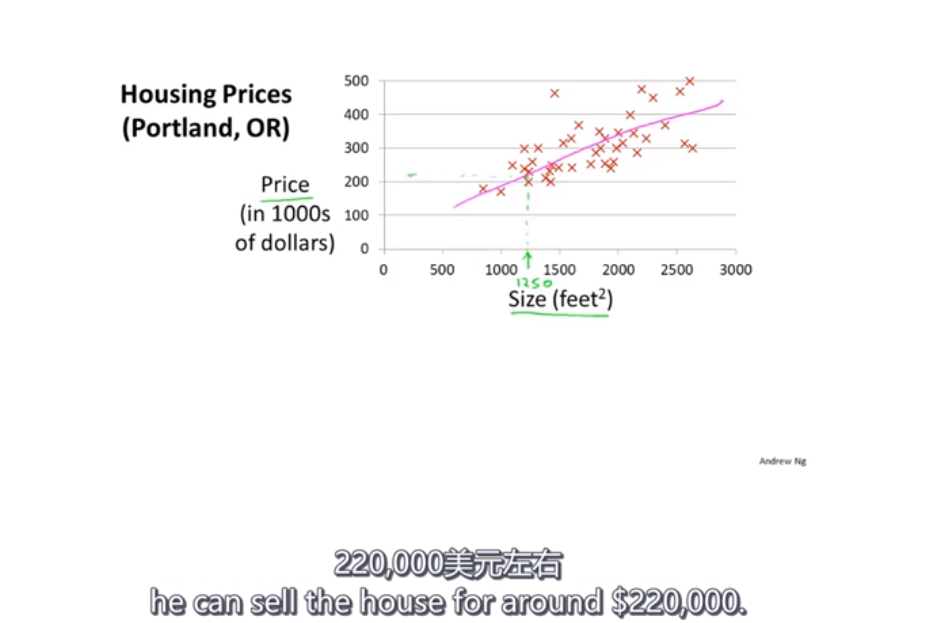
数据集，也就是训练集，从这个训练集中学习如何预测房价

 

 

 

 

 

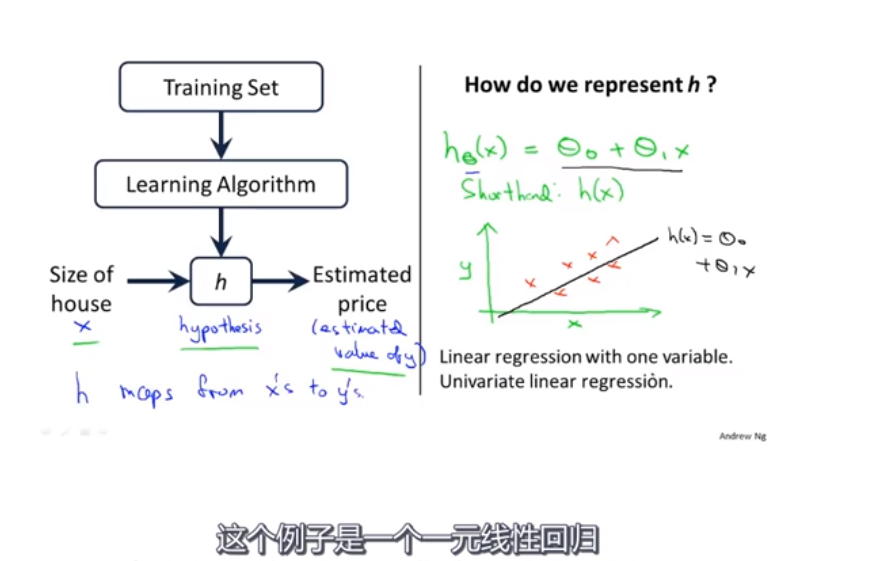
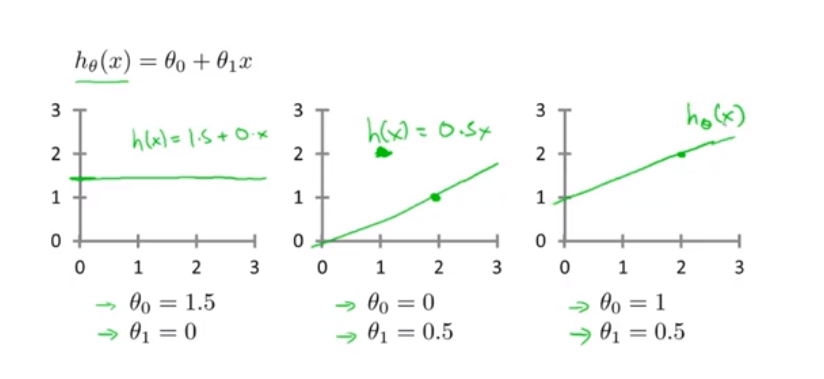
玄学调参来了

 

 

 

 

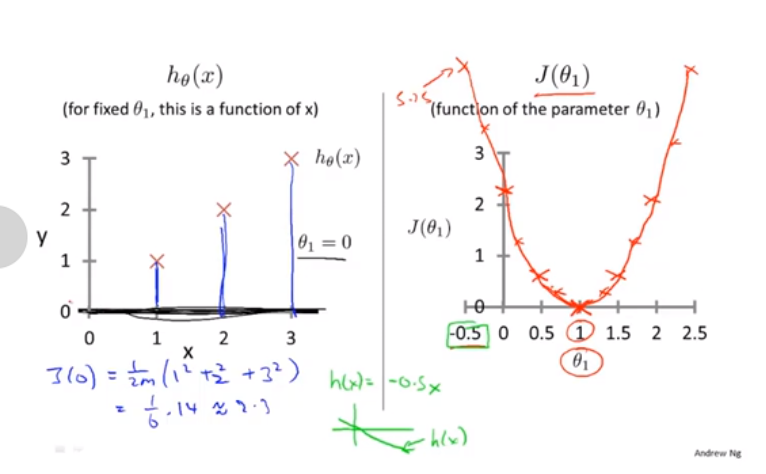
代价函数就是这个误差平方差函数

找到使得方差最小的θ1和θ0，也就是函数J(θ0,θ1)

平方值还有一个好处就是如果hx-y等于负数，它的平方还是正数，不会导致总体值变小

 

 

简化

 

 

绘制代价函数！

很明显代价函数为0时，是最好的。

一般就是最小值的时候最合适

 

 

 

 

 

两个参数的情况下

 

 

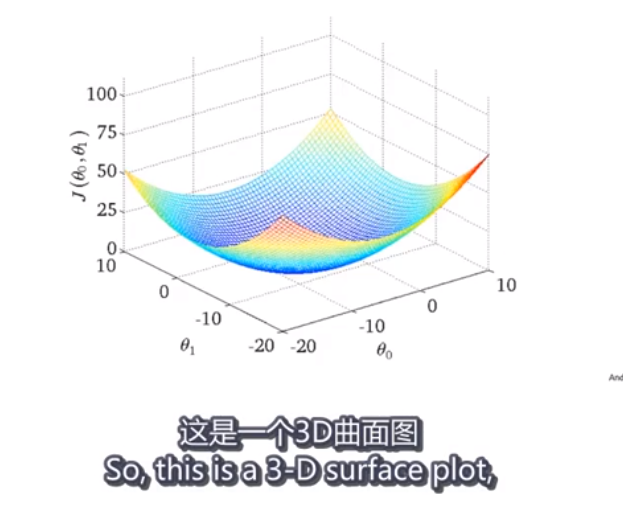
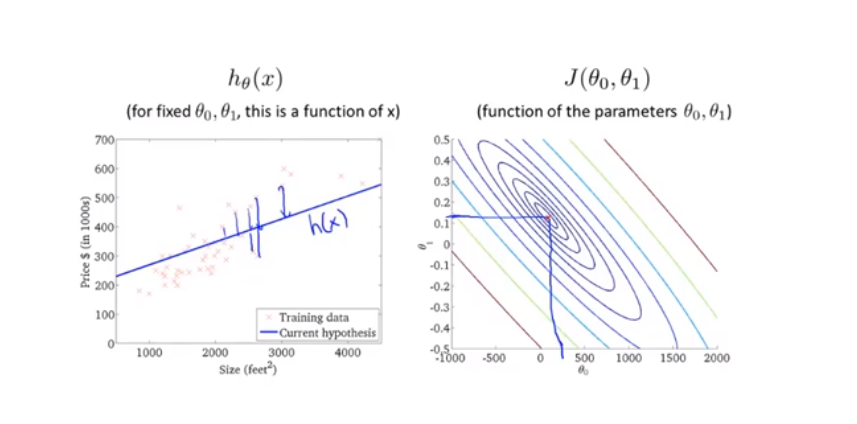
以后参数多了的话，图像的维度会更高，很多都画不出来的。

 

自动找到代价函数J，最小值的参数的方法。

 

梯度下降法

 

 

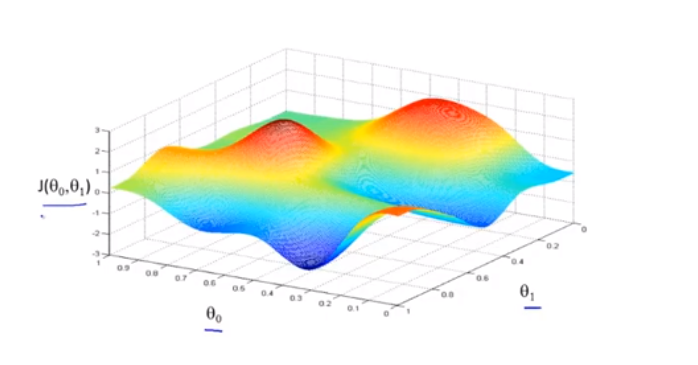
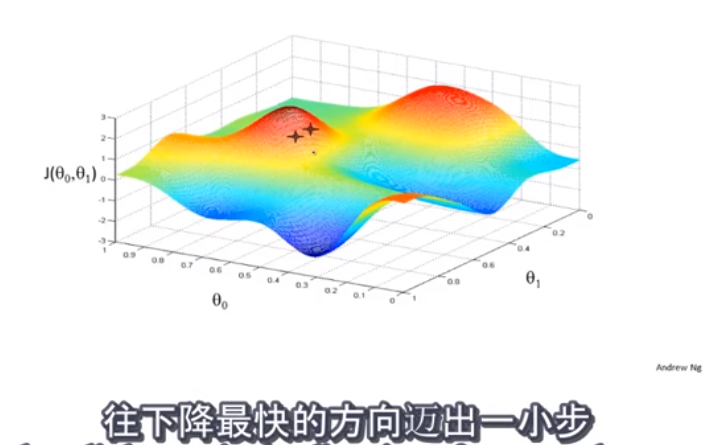
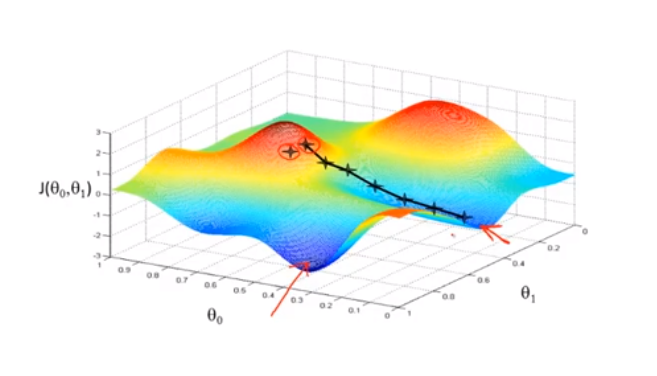
这个是偏导数，求面上一点的斜率

偏导数 f'x(x0,y0) 表示固定面上一点对 x 轴的切线斜率；偏导数 f'y(x0,y0) 表示固定面上一点对 y 轴的切线斜率。 

 

 发现这是个很好的思路，不要想着一开始就找出能够根本解决问题的通法。

而是基于问题的实际情况，一步步找到近似解

 

 

 

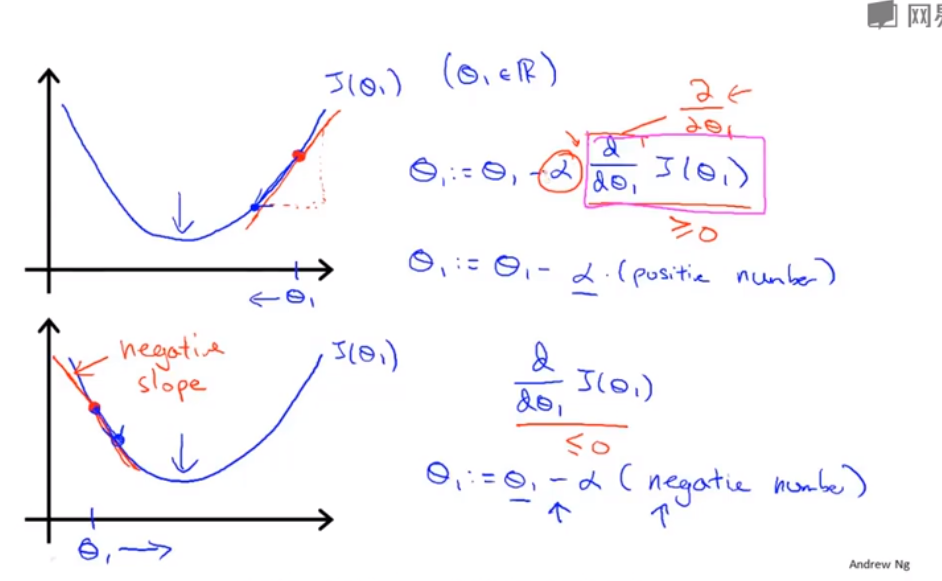
导数项的意义

 

 

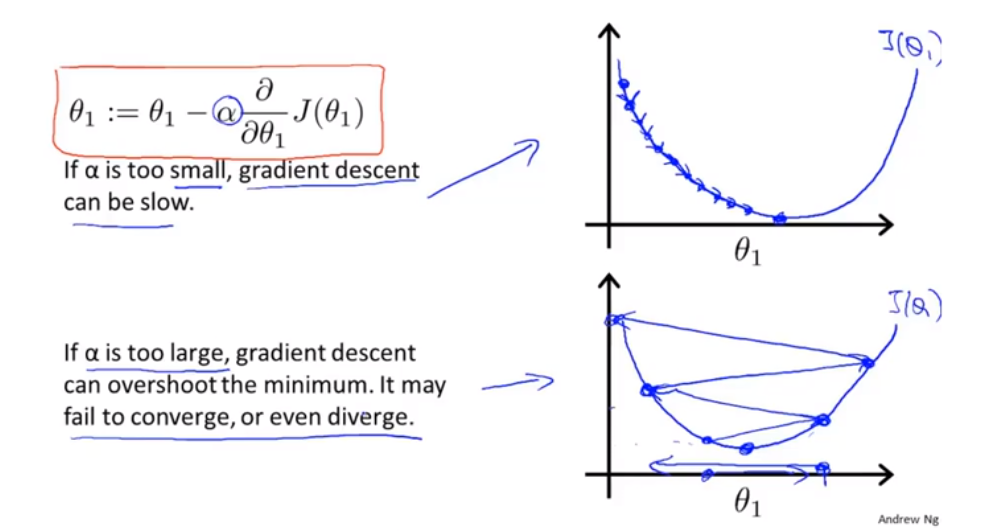
a太小，步伐太小，需要走很多步！

a太大，可能错过最小点，最后无法收敛。

 

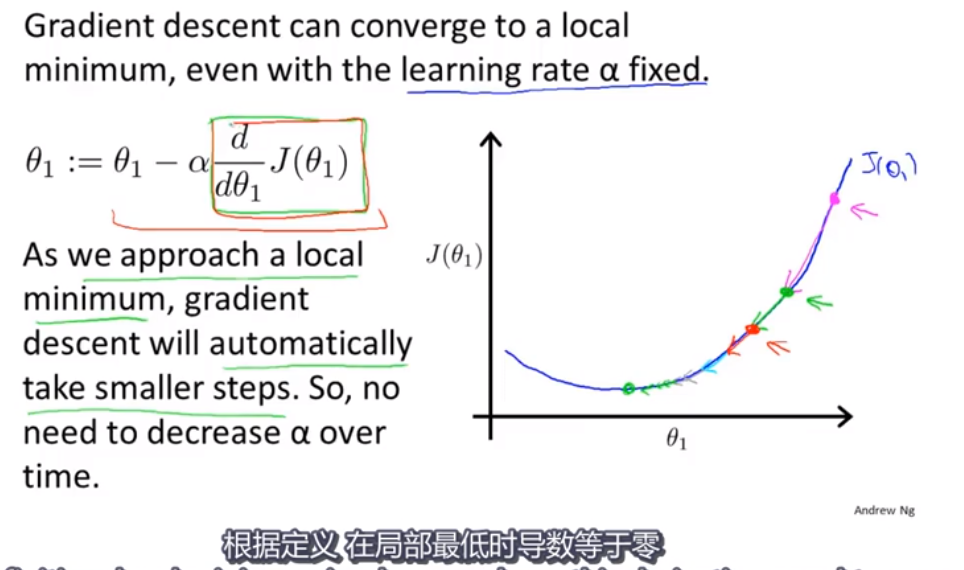
如果开始就是最低点呢？下一步梯度下降会怎样？

局部最低点！ 导数为0！

 

 

越接近最小值，导数越来越小，变化就越来越平缓，步数越来越慢

 

 

 

梯度下降+代价函数-》线性回归

 

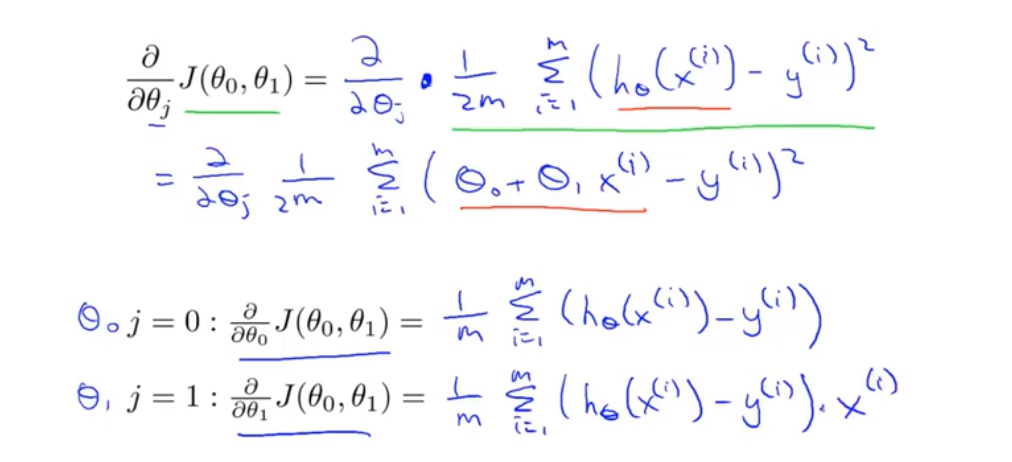
容易陷入局部最优

但是线性回归的代价函数总是这样的，肯定会收敛到最低点

只要使用梯度下降，就能找到

 

 

每次都遍历了整个训练集

 

梯度下降适合更大规模的数据集