5G NR系列（四）物理下行共享信道（PDSCH）物理层过程详解

一、传输块CRC附加

（一） 方法步骤

通过循环冗余校验(CRC)在每个传输块上提供错误检测。
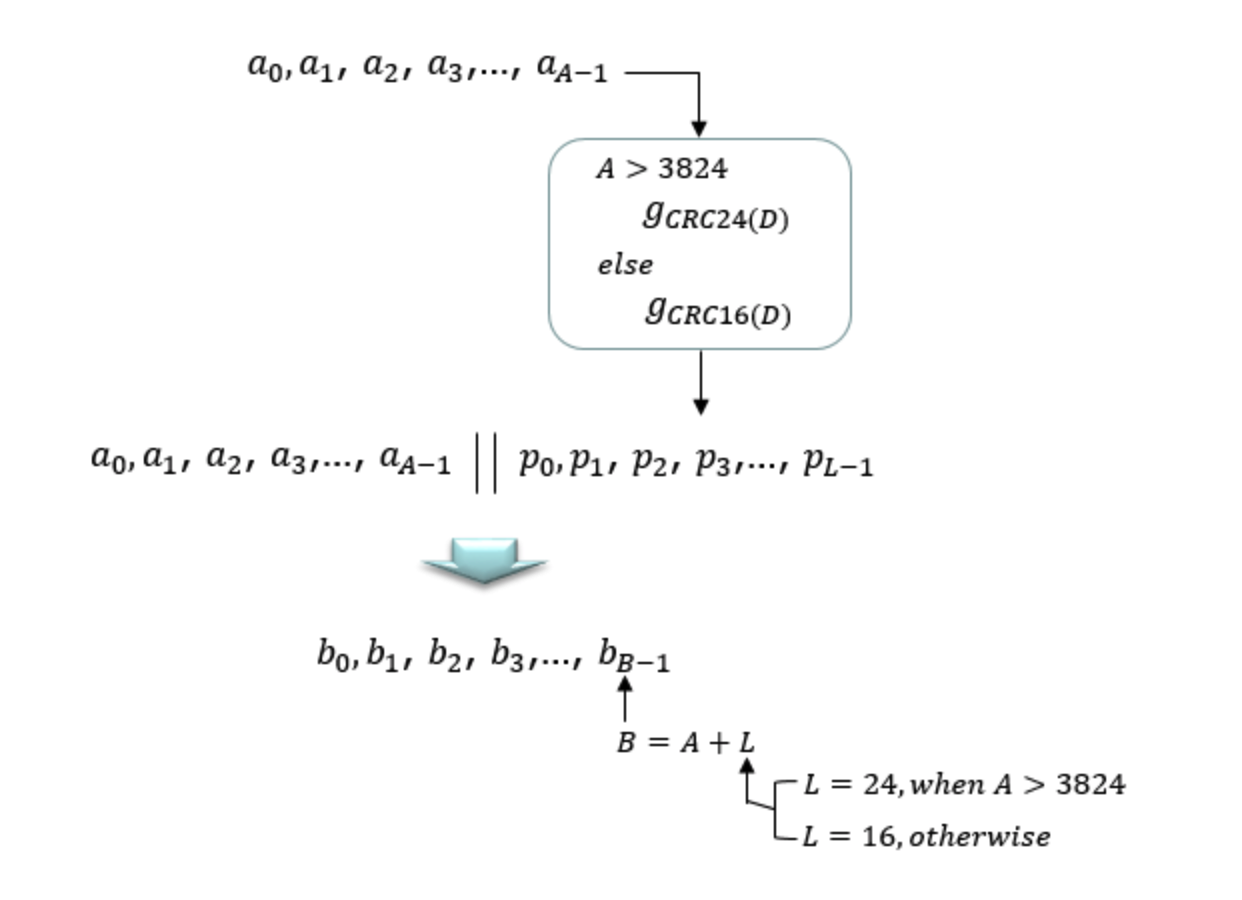
整个传输块用于计算CRC奇偶校验比特。传送到层1的传输块比特记为\(a_{0}, a_{1}, a_{2}, a_{3}, \dots, a_{A-1}\)，奇偶校验比特记为\(p_{0}, p_{1}, p_{2}, p_{3}, \dots, p_{L-1}\)，其中\(A\)是有效载荷的大小，\(L\)是校验比特的位数。最低阶信息位\(a_{0}\)被映射到传输块的最有效位。
奇偶校验位根据协议所述规则计算并附加到DL-SCH传输块。当\(A>3824\)时，设置\(L\)为24比特，并使用生成多项式\(g_{\mathrm{CRC} 24 \mathrm{A}}(D)\)；否则，设置\(L\)为16比特，并使用生成多项式\(g_{\mathrm{CRCl} 6}(D)\)。
CRC附加之后的比特记为\(b_{0}, b_{1}, b_{2}, b_{3}, \ldots, b_{B-1}\)，其中\(B=A+L\)。

（二）流程图

二、码块分割及CRC附加

（一）方法步骤

码块分割的输入比特序列记为\(b_{0}, b_{1}, b_{2}, b_{3}, \dots, b_{B-1}\)，其中\(B>0\)。如果\(B\)大于最大码块长度\(K_{\mathrm{cb}}\)，则需要进行码块分割，并对分割后得到的各个码块添加24比特CRC校验序列。
码块分割的输出比特记为\(c_{r 0}, c_{r 1}, c_{r 2}, c_{r 3}, \dots, c_{r\left(K_{r}-1\right)}\)，其中\(0 \leq r<C\)表示码块编号，\(K_{r}=K\)表示每个码块中的比特数。

1.确定最大码块长度\(K_{\mathrm{cb}}\)

• 对于BG1，最大码块长度为：\(K_{\mathrm{cb}}=8448\)
• 对于BG2，最大码块长度为：\(K_{\mathrm{cb}}=3840\)

2.确定码块数\(C\)

• 当\(B \leq K_{\mathrm{cb}}\)时，不需要进行码块分割，即码块数\(C=1\)，码块长度\(B^{\prime}=B\)，不添加CRC，\(L=0\)。
• 当\(B\)超过\(K_{\mathrm{cb}}\)时，需要进行码块分割，码块数\(C=\left\lceil B /\left(K_{c b}-L\right)\right\rceil\)，（5G NR规定采用等长分割），分割之后总的传输块长度为\(B^{\prime}=B+C \cdot L\)，\(L=24\)。

3.确定每个码块中的比特数\(K\)

• \(K^{\prime}=B^{\prime} / C\)；
• 对于BG1，\(K_{b}=22\)；对于BG2，需要根据\(B\)的大小决定：当\(B>640\)时，\(K_{b}=10\)；当\(B>560\)时，\(K_{b}=9\)；当\(B>192\)时，\(K_{b}=8\)；否则，\(K_{b}=6\) 。然后，根据表5.3.2-1找到最小的\(Z\)值（用\(Z_{c}\)表示），使其满足\(K_{b} \cdot Z_{c} \geq K^{\prime}\)，并令\(K=22 Z_{c}\)（对于BG1），或者\(K=10 Z_{c}\)（对于BG2）。

4.计算码块分割及CRC添加后的比特序列\(\mathcal{C}_{r k}\)

• 当不分割时，不添加CRC。
• 当码块数\(C>1\)时，输入序列根据码块数进行等长分割，每段根据生成多项式\(g_{\mathrm{CRC} 24 \mathrm{B}}(D)\)计算CRC校验序列，并分别附加在各段之后。
• 最后在剩余的位置插入填充比特\(c_{r k}=<N U L L>\)。

（二）流程图

三、LDPC编码

（一）方法步骤

码块被传送到信道编码模块。码块中的比特记为\(\mathcal{C}_{r 0}, \mathcal{C}_{r 1}, \mathcal{C}_{r 2}, \mathcal{C}_{r 3}, \ldots, \mathcal{C}_{r}\left(K_{r}-1\right)\)，其中\(r\)表示码块编号，\(K_{r}\)表示码块\(r\)中的比特数。码块总数记为\(C\)，每个码块单独进行LDPC编码。
编码后的比特记为\(d_{r 0}, d_{r 1}, d_{r 2}, d_{r 3}, \ldots, d_{r\left(N_{r}-1\right)}\)。

（二）流程图

伪代码如下：

输入：in-待编码的码块段；bgn-基图编号（1或2）
输出：out-LDPC编码后的结果
1）根据bgn取值和输入码块段长度确定Zc，根据bgn及Zc确定编码后的输出比特长度N；
2）将输入中由-1表示的每个填充位替换为0；
3）编码生成完整的LDPC码字
根据Zc的值确定索引值setIdx，38.212表5.3.2-1；
根据bgn和setIdx确定校验矩阵V，38.212表5.3.2-2和表5.3.2-3；
根据V矩阵和ZC计算移位矩阵P，P=mod(V, ZC)；
for每个码块段：
	计算校验比特位；
	生成完整LDPC码字
end for
4）将每个填充位再次替换为-1；
5）截断前2*Zc个比特,得到最后输出结果out。

四、速率匹配

（一）方法步骤

每个码块编码后的比特记为\(d_{r 0}, d_{r 1}, d_{r 2}, d_{r 3}, \ldots, d_{r\left(N_{r}-1\right)}\)，被传送到速率匹配模块，其中\(r\)表示码块编号，\(N_{r}\)表示码块\(r\)中编码后的比特数。码块总数记为\(C\)，每个码块单独进行速率匹配，设置\(I_{L B R M}=1\)。
速率匹配后的比特记为\(f_{r 0}, f_{r 1}, f_{r 2}, f_{r 3}, \ldots, f_{r\left(E_{r}-1\right)}\)，其中\(E_{r}\)表示码块\(r\)速率匹配后的比特数。

（二）流程图

五、码块连接

（一）方法步骤

码块连接模块的输入比特序列是序列\(f_{r 0}, f_{r 1}, f_{r 2}, f_{r 3}, \ldots, f_{r\left(E_{r}-1\right)}\)，\(r=0, \ldots, C-1\)，其中\(E_{r}\)表示第\(r\)个码块速率匹配后的比特数。码块连接模块的输出比特序列是序列\(g_{0}, g_{1}, g_{2}, g_{3}, \dots, g_{G-1}\)，其中\(G\)表示用于传输的编码比特的总数。
码块连接就是按顺序连接不同码块速率匹配的输出。

六、加扰

（一）方法步骤

最多可以传输两个码字 \(q \in\{0,1\}\) 。在单码字传输的情况下，\(q=0\) 。
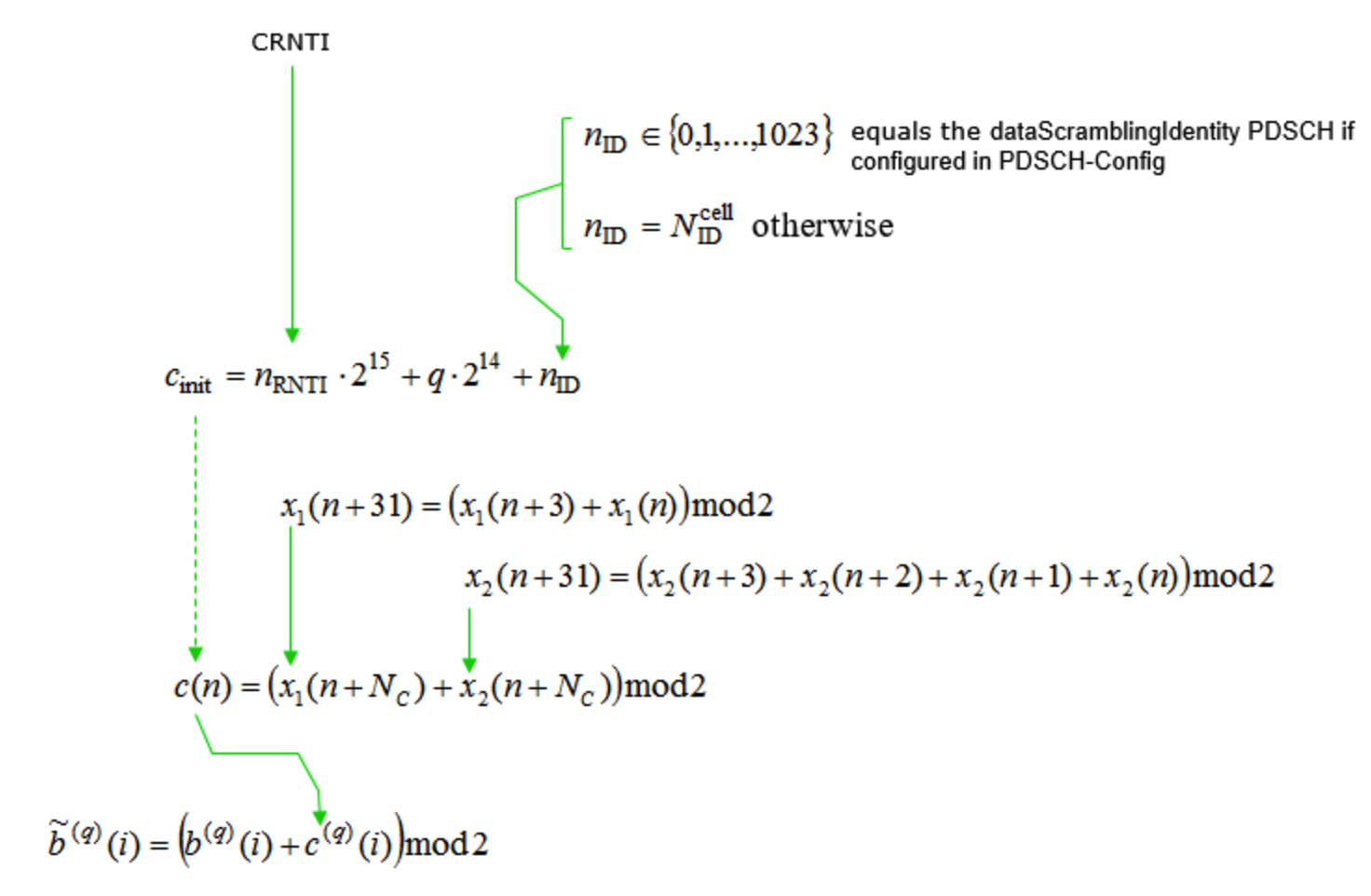
对于每个码字 \(q\) ，UE应假设比特块 \(b^{(q)}(0), \ldots, b^{(q)}\left(M_{\mathrm{bit}}^{(q)}-1\right)\) 在调制之前被加扰，\(M_{\mathrm{bit}}^{(q)}\) 是在物理信道中传输的码字 \(q\) 的比特数量，根据如下公式产生一个加扰比特块 \(\tilde{b}^{(q)}(0), \ldots, \tilde{b}^{(q)}\left(M_{\mathrm{bit}}^{(q)}-1\right)\) ：

\[\widetilde{b}^{(q)}(i)=\left(b^{(q)}(i)+c^{(q)}(i)\right) \bmod 2 \]

式中，加扰序列 \(c^{(q)}(i)\) 由5.2.1节给出。加扰序列生成器应按照如下公式初始化：

\[c_{\text {init }}=n_{\mathrm{RNTI}} \cdot 2^{15}+q \cdot 2^{14}+n_{\mathrm{ID}} \]

式中，

• \(n_{\mathrm{ID}} \in\{0,1, \ldots, 1023\}\) 等于高层参数dataScramblingIdentityPDSCH（如果配置），并且RNTI等于C-RNTI、MCS-C-RNTI或CS-RNTI，并且在公共搜索空间中不使用DCI格式1_0调度传输，
• 否则，\(n_{\mathrm{ID}}=N_{\mathrm{ID}}^{\mathrm{cell}}\)

（二）流程图

七、调制

（一）方法步骤

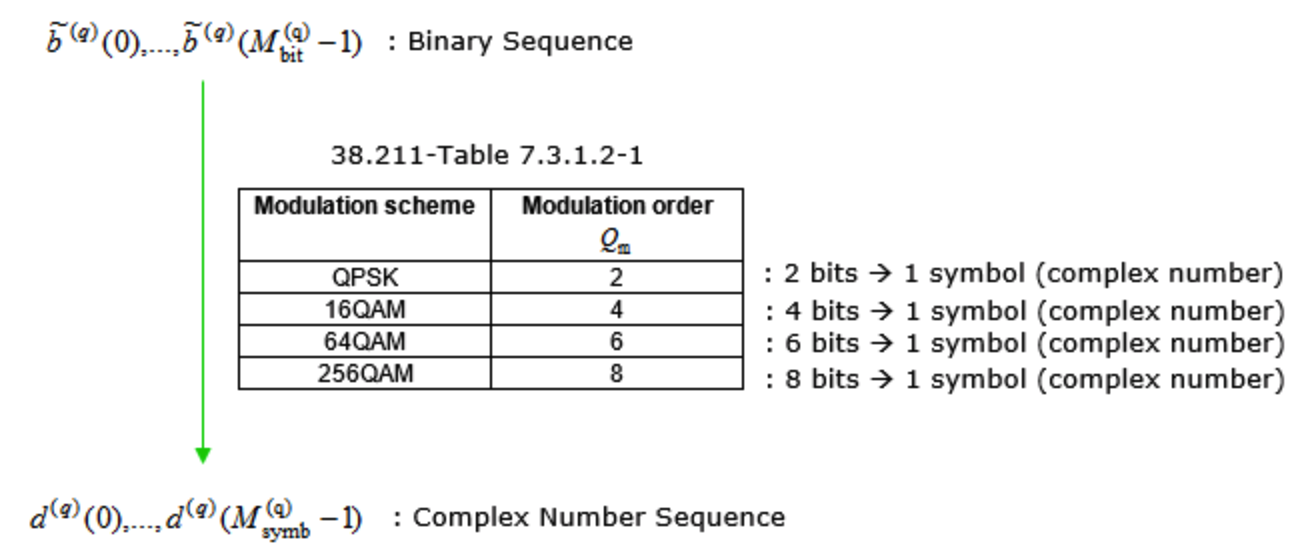
对于每个码字 \(q\) ，UE应假设加扰比特块 \(\tilde{b}^{(q)}(0), \ldots, \tilde{b}^{(q)}\left(M_{\mathrm{bit}}^{(q)}-1\right)\) 使用下表中的一种调制格式进行调制，产生一个复数值调制符号块 \(d^{(q)}(0), \ldots, d^{(q)}\left(M_{\mathrm{symb}}^{(q)}-1\right)\) 。

支持的调制格式

调制格式	阶数
QPSK	2
16QAM	4
64QAM	6
256QAM	8

（二）流程图

八、层映射

（一）方法步骤

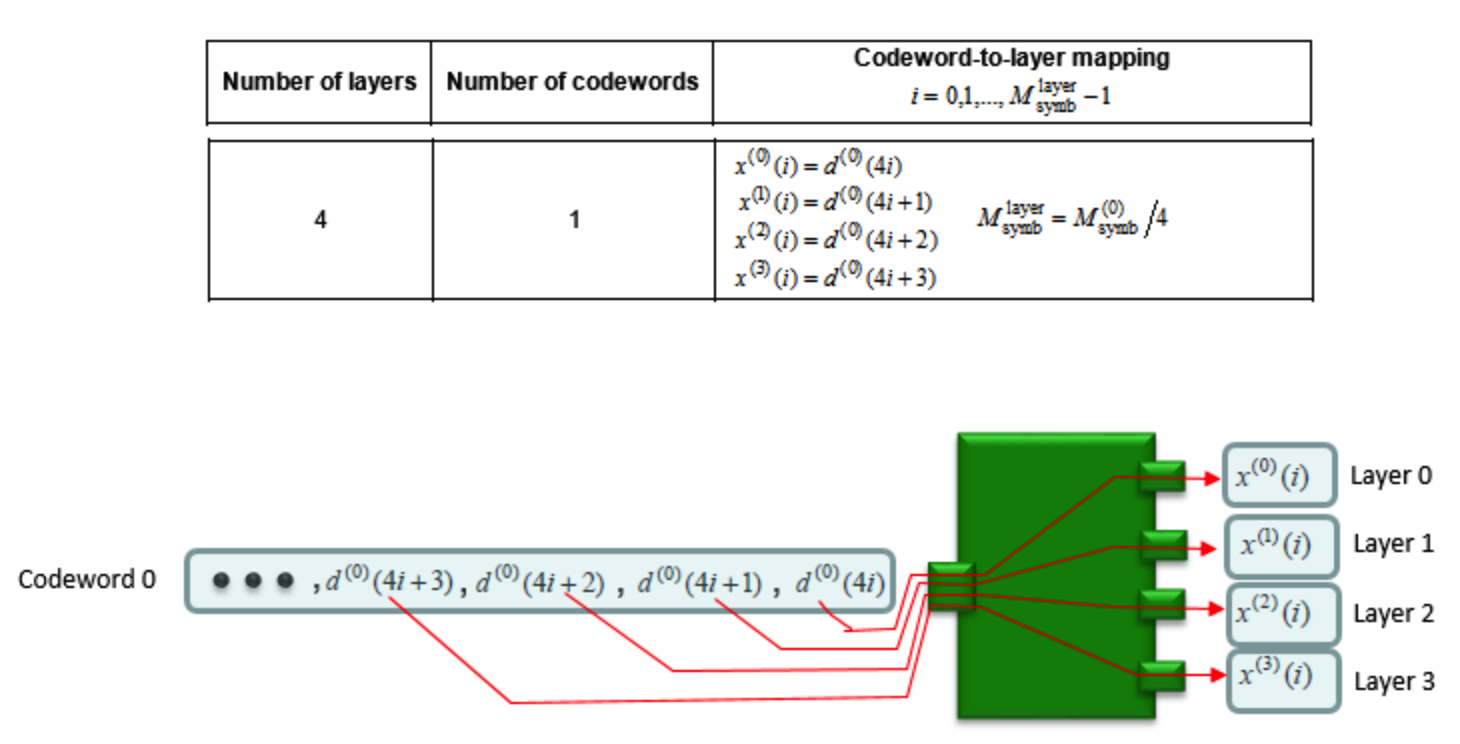
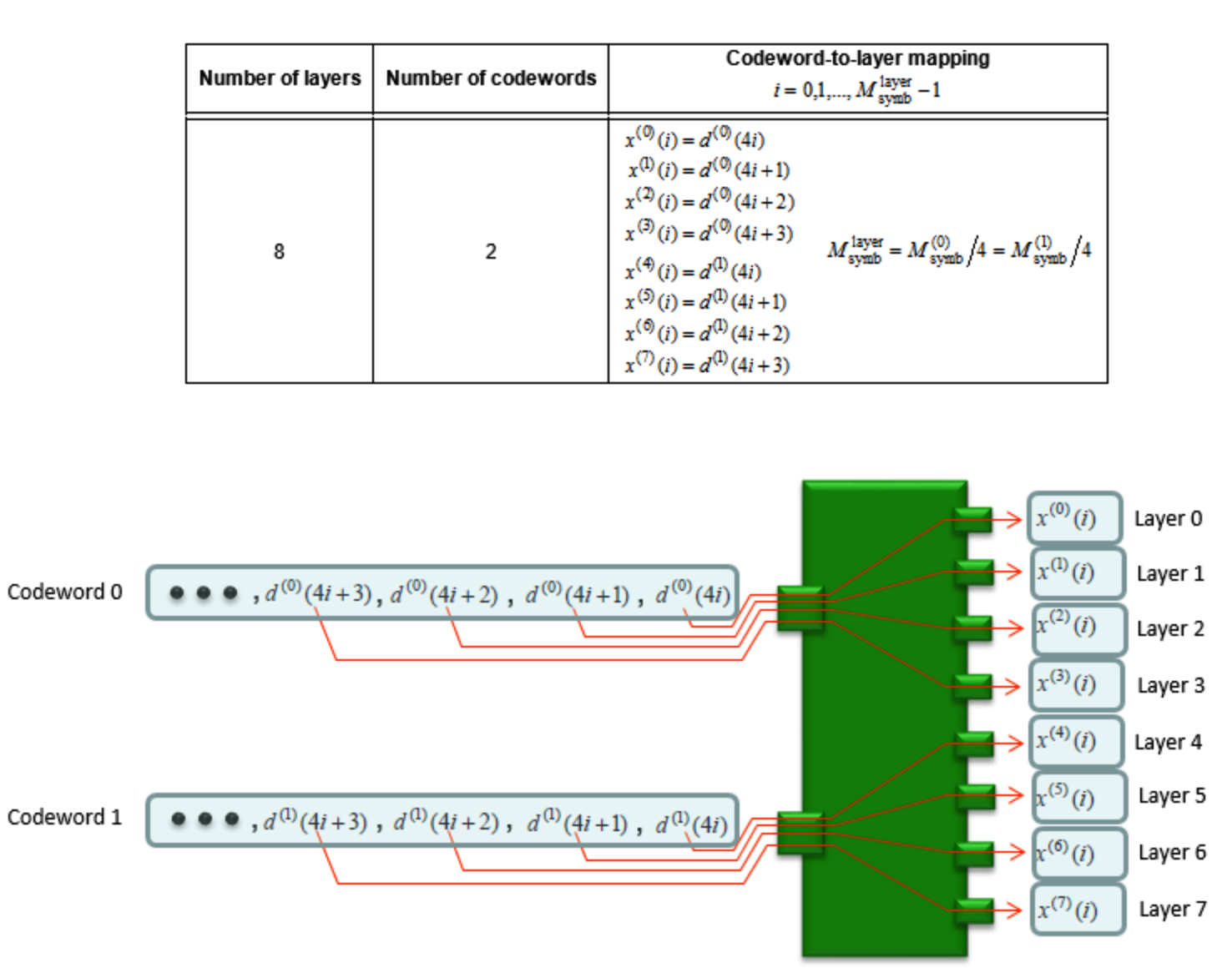
UE应假设根据下表将要发送的每个码字的复数值调制符号映射到一个或多个层上。码字 \(q\) 的复数值调制符号 \(d^{(q)}(0), \ldots, d^{(q)}\left(M_{\mathrm{symb}}^{(q)}-1\right)\) 应映射到层 \(x(i)=\left[\begin{array}{lll}{x^{(0)}(i)} & {\dots} & {x^{(\nu-1)}(i)}\end{array}\right]^{T}\) 上，\(i=0,1, \ldots, M_{\mathrm{symb}}^{\mathrm{layer}}-1\)，式中 \(v\) 是层数，\(M_{\mathrm{symb}}^{\mathrm{layer}}\) 是每层调制符号数。

空分复用的码字-层映射

层数	码字数	码字-层映射$$i=0,1, \ldots, M_{\mathrm{symb}}^{\mathrm{layer}}-1$$
1	1	\(x^{(0)}(i)=d^{(0)}(i)\)，\(M_{\mathrm{symb}}^{\mathrm{layer}}=M_{\mathrm{symb}}^{(0)}\)
2	1	\(\begin{array}{l}{x^{(0)}(i)=d^{(0)}(2 i)} \\ {x^{(1)}(i)=d^{(0)}(2 i+1)}\end{array}\)，\(M_{\mathrm{symb}}^{\mathrm{layer}}=M_{\mathrm{symb}}^{(0)} / 2\)
3	1	\(\begin{array}{l}{x^{(0)}(i)=d^{(0)}(3 i)} \\ {x^{(1)}(i)=d^{(0)}(3 i+1)} \\ {x^{(2)}(i)=d^{(0)}(3 i+2)}\end{array}\)，\(M_{\mathrm{symb}}^{\mathrm{layer}}=M_{\mathrm{symb}}^{(0)} / 3\)
4	1	\(\begin{array}{l}{x^{(0)}(i)=d^{(0)}(4 i)} \\ {x^{(1)}(i)=d^{(0)}(4 i+1)} \\ {x^{(2)}(i)=d^{(0)}(4 i+2)} \\ {x^{(3)}(i)=d^{(0)}(4 i+3)}\end{array}\)，\(M_{\mathrm{symb}}^{\mathrm{layer}}=M_{\mathrm{symb}}^{(0)} / 4\)
5	2	\(\begin{array}{l}{x^{(0)}(i)=d^{(0)}(2 i)} \\ {x^{(1)}(i)=d^{(0)}(2 i+1)} \\ {x^{(2)}(i)=d^{(1)}(3 i)} \\ {x^{(3)}(i)=d^{(1)}(3 i+1)} \\ {x^{(4)}(i)=d^{(1)}(3 i+2)}\end{array}\)，\(M_{\mathrm{symb}}^{\mathrm{layer}}=M_{\mathrm{symb}}^{(0)} / 2=M_{\mathrm{symb}}^{(1)} / 3\)
6	2	\(\begin{array}{l}{x^{(0)}(i)=d^{(0)}(3 i)} \\ {x^{(1)}(i)=d^{(0)}(3 i+1)} \\ {x^{(2)}(i)=d^{(0)}(3 i+2)} \\ {x^{(3)}(i)=d^{(1)}(3 i)} \\ {x^{(4)}(i)=d^{(1)}(3 i+1)} \\ {x^{(5)}(i)=d^{(1)}(3 i+2)}\end{array}\)，\(M_{\mathrm{symb}}^{\mathrm{layer}}=M_{\mathrm{symb}}^{(0)} / 3=M_{\mathrm{symb}}^{(1)} / 3\)
7	2	\(\begin{array}{l}{x^{(0)}(i)=d^{(0)}(3 i)} \\ {x^{(1)}(i)=d^{(0)}(3 i+1)} \\ {x^{(2)}(i)=d^{(0)}(3 i+2)} \\ {x^{(3)}(i)=d^{(1)}(4 i)} \\ {x^{(4)}(i)=d^{(1)}(4 i+1)} \\ {x^{(5)}(i)=d^{(1)}(4 i+2)} \\ {x^{(6)}(i)=d^{(1)}(4 i+3)}\end{array}\)，\(M_{\mathrm{symb}}^{\mathrm{layer}}=M_{\mathrm{symb}}^{(0)} / 3=M_{\mathrm{symb}}^{(1)} / 4\)
8	2	\(\begin{array}{l}{x^{(0)}(i)=d^{(0)}(4 i)} \\ {x^{(1)}(i)=d^{(0)}(4 i+1)} \\ {x^{(2)}(i)=d^{(0)}(4 i+2)} \\ {x^{(3)}(i)=d^{(0)}(4 i+3)} \\ {x^{(3)}(i)=d^{(0)}(4 i)} \\ {x^{(4)}(i)=d^{(1)}(4 i+1)} \\ {x^{(6)}(i)=d^{(1)}(4 i+2)} \\ {x^{(7)}(i)=d^{(1)}(4 i+3)}\end{array}\)，\(M_{\mathrm{symb}}^{\mathrm{layer}}=M_{\mathrm{symb}}^{(0)} / 4=M_{\mathrm{symb}}^{(1)} / 4\)

（二）流程图

未完待续......